Magnetväli

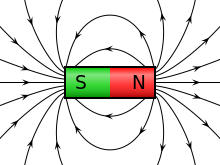
Magnetväli on füüsikaline väli, mis avaldub jõuna liikuvatele elektrilaengutele ja samuti magnetmomenti omavatele kehadele (sel juhul sõltumata nende liikumisolekust).

Magnetvälja tekitamiseks on olemas kaks eri viisi. Esimene võimalus on kasutada elektrilaengute liikumist, näiteks juhet läbivat elektrivoolu (vt Biot'-Savarti seadus). Magnetvälja tekkimist elektrilaengute liikumisel võib seletada laengutevaheliste elektrostaatiliste jõudude mõjuga. Sel viisil saab valmistada näiteks elektromagneteid.

Teine võimalus põhineb elementaarosakestel, millel on seesmine võime (spinn) tekitada enda ümber magnetmomenti^{[nb 1]}. Teatud materjalides – ferromagneetikutes – elektronide magnetväljad liituvad ja materjali ümbritsevas keskkonnas on summaarne väli. Sellise liitumise tulemusena tekib püsimagnet.^[1]

Magnetväli on vektorväli, mis tähendab, et välja iseloomustab igas tema punktis ja igal hetkel vektori väärtus, seega tema suurus (see näitab, kui suurt jõudu väli avaldab) ja suund (mis suunas jõud mõjub).^{[nb 2]}.

Magnetväljal on palju kasutusalasid, seda nii kauges minevikus kui ka tänapäeval. Maa magnetvälja on juba sajandeid kasutatud navigeerimisel. Pöörlev magnetväli on kasutusel näiteks elektrimootoris ja elektrigeneraatoris. Magnetjõud annavad teavet laengukandjate kohta eri materjalides Halli efekti kaudu.

Ajalugu

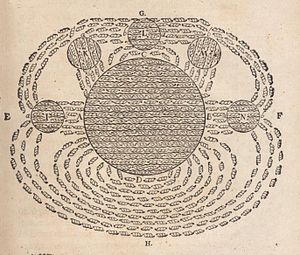
Kuigi magnetid ja magnetism olid teada juba pikka aega, algas selle põhjalikum uurimine aastal 1269, kui Prantsuse teadlane Petrus Peregrinus de Maricourt „kaardistas“ magnetvälja sfäärilise magneti pinnal, kasutades raudnõelu^{[nb 3]}. Märgates, et väljajooned ristusid kahes punktis, nimetas ta neid punkte poolusteks analoogselt Maa poolustega. Peaaegu kolm sajandit hiljem imiteeris William Gilbert Colcheterist Petrus Peregrinuse tööd ja oli esimene, kes märkis selgesõnaliselt, et ka Maa on magnet.^[2] 1600. aastal avaldatud Gilbert'i töö "De Magnete" aitas kaasa magnetismi kui teaduse loomisel.

1750. aastal märkis John Michell, et magnetvälja poolused tõmbuvad ja tõukuvad pöördvõrdeliselt kauguse ruuduga.^[3] Charles-Augustin de Coulomb kontrollis seda katseliselt 1785. aastal ja märkis, et põhja- ja lõunapoolusi ei saa lahutada.^[4] Tuginedes poolusevahelistele jõule lõi Siméon-Denis Poisson (1781–1840) esimese magnetvälja mudeli, mida ta tutvustas 1824. aastal.^[5] Selles mudelis on magnetväli tekitatud magnetpooluste poolt ja magnetism on tingitud väikeste põhja-lõunapooluste paaride poolt.

Kolm avastust viisid magnetismi teadusharu loomiseni. Esiteks, 1819. aastal avastas Hans Christian Ørsted, et elektrivool tekitab seda ümbritseva magnetvälja. Edasi, aastal 1820 näitas André-Marie Ampère, et kaks paralleelset juhet, milles on samasuunaline elektrivool, tõmbuvad. Viimaks Jean-Baptiste Biot ja Félix Savart avastasid 1820. aastal seaduse, mis kujutab õigesti voolu all oleva juhtme ümber olevat magnetvälja. See Biot'-Savarti seadus on tuntud ka Biot'-Savarti-Laplace'i seadusena, sest Pierre-Simon Laplace sõnastas selle üldkujul.

Laiendades neid eksperimente, avaldas Ampère oma mudeli magnetismi kohta aastal 1825. Seal näitas ta elektrivoolu ja magnetite samaväärsust^[6] ja püstitas hüpoteesi, et magnetism on tingitud püsivast elektrivoolust, mitte Poissoni magnetilise dipooli mudelist^{[nb 4]}. See võimaldas ka seletada, miks magnetlaengut ei saa isoleerida. Lisaks tuletas Ampère nii Ampère'i jõu seaduse, mis kirjeldab jõude kahe voolujuhtme vahel, kui ka Ampère'i seaduse, mis nagu ka Biot'-Savart'i seadus kirjeldab täpselt magnetvälja tekkimist ühtlase voolu korral. Selles töös võttis Ampère elektri ja magnetismi vaheliste seoste kirjeldamiseks kasutusele termini "elektrodünaamika".

Aastal 1831 avastas Michael Faraday elektromagnetilise induktsiooni, kui leidis, et muutuv magnetväli tekitab ümbritseva elektrivälja. Ta kirjeldas seda nähtust Faraday induktsiooniseadusena. Pärast seda tõestas Franz Ernst Neumann, et magnetväljas liikuva elektrijuhi jaoks on induktsioon Ampère'i jõu tagajärg.^[7] Selle protsessi käigus tutvustas ta magnetvälja potentsiaali vektorit, mis hiljem osutus samaväärseks Faraday pakutud tekkemehhanismiga.

1850. aastal eristas lord Kelvin (sel ajal tuntud kui William Thomson) kahte magnetvälja parameetrit, mida nüüd tunneme kui magnetvälja tugevust H ja magnetinduktsiooni B. Esimene rakendub Poissoni mudelile ja teine Ampère'i induktsiooni mudelile.^[8] Veel enamgi, ta tuletas, kuidas H ja B omavahel seotud on.

Aastatel 1861–1865 arendas ja avaldas James Clerk Maxwell Maxwelli võrrandid, mis selgitasid ja ühendasid klassikalised elektri ja magnetismi teooriad. Esimest korda avaldati need artiklis "On Physical Lines of Force" aastal 1861. Need võrrandid kehtisid, kuigi olid puudulikud. Maxwell esitas oma täiustatud võrrandid 1865. aastal artiklis "Elektromagnetvälja dünaamiline teooria" ja esitas väite, et valgus on elektromagnetlaine. Heinrich Hertz kinnitas eksperimentaalselt seda aastal 1887.

Kui Ampère'i jõu seaduses oli magnetvälja jõud liikuvale elektrilaengule ebatäpselt ja mitte kuigi detailselt seletatud, siis 1892. aastal parandas Hendrik Lorentz selle, tuginedes Maxwelli võrranditele.^[9] Sellega sai viimane tükk klassikaline elektrodünaamika teooria puslesse lisatud.

20. sajandil laiendati elektrodünaamika teooriat, kuhu lisati ka relatiivsusteooria ja kvantmehaanika. Albert Einstein näitas oma 1905. aasta artiklis, mis tutvustas relatiivsusteooriat, et nii elekter kui ka magnetism on sama nähtuse osad, vaadelduna erinevast taustsüsteemist. Lõpuks ühendati ka kvantmehaanika ja elektrodünaamika kvantelektrodünaamikaks.

Magnetvälja iseloomustad suurusused ja mõõtühikud

Pikemalt artiklis Magnetiline induktsioon

Magnetvälja põhiparameeter on magnetinduktsiooni vektor $\mathbf {B}$ (vektoreid tähistatakse sageli ka noolega tähe peal: ${\vec {B}}$ ). Magnetinduktsioon (ehk magnetiline induktsioon ehk magnetvälja tihedus) väljendab jõudu, mida magnetväli avaldab liikuvatele elektrilaengutele, täpsemalt nende magnetmomendile. See jõud $\mathbf {F}$ on võrdeline laengu suurusega q ning laengu kiiruse $\mathbf {v}$ ja magnetinduktsiooni $\mathbf {B}$ vektorkorrutisega $\mathbf {v} \times \mathbf {B}$ :

\mathbf {F} =q(\mathbf {v} \times \mathbf {B} ).

Niisugune jõud koos elektrivälja jõuga (vt Lorentzi jõud) toimib ka juhtmele, mida läbib elektrivool, mis teatavasti on elektrilaengute suunatud liikumine.

Magnetinduktsiooni mõõtühik SI-süsteemis on tesla (tähis T). Teslat saab avaldada teiste SI ühikute abil näiteks järgmiselt:

\mathrm {1\,T=1\,{\frac {N}{A\,m}}=1\,{\frac {Wb}{m^{2}}}} ,

kus N on jõu ühik njuuton, A on voolutugevuse ühik amper, m on pikkuse ühik meeter ja Wb on magnetvoo ühik veeber.

CGS-süsteemis mõõdetakse magnetinduktsiooni gaussides (tähis G). 1 G = 1·10⁻⁴ T.

Magnetinduktsiooni kõrval on magnetvälja kirjeldamisel kasutusel ka magnetvälja tugevus $\mathbf {H}$ . See suurus väljendab magnetvälja jõudu vaakumis (seal puudub magneeditav keskkond). Sel juhul erineb magnetväljatugevus magnetinduktsioonist (SI ühikute kasutamisel) ainult magnetilise konstandi $\mu _{0}$ kordselt:

\mathbf {B} =\mu _{0}\mathbf {H}

.

CGS-süsteemis $\mathbf {B} =\mathbf {H}$ .

Füüsikalises kehas (materjalis) väljendatakse seda seost magneetumuse $\mathbf {M}$ kaudu:

\mathbf {B} =\mu _{0}\left(\mathbf {H} +\mathbf {M} \right)\ =\mu \mathbf {H} ,

kus $\mu$ on materjali magnetiline läbitavus.

Magnetvälja tugevust võib vaadelda välise, magneetiva väljana, mis tekitab (indutseerib) materjali sees jõu, mida nimetatakse magnetinduktsiooniks.

Vektorvälja H mõõdetakse SI-süsteemis amprites meetri kohta (A/m). CGS-süsteemis on vastav ühik örsted (tähis Oe). 1 Oe = 1000/(4π) A/m ≈ 79,5775 A/m.

Magnetvälja mõõteriist on magnetomeeter.

Tuleb tähele panna, et sageli nimetatakse magnetvälja tugevuseks ka teslades mõõdetavat suurust (näiteks Maa magnetvälja korral).

Magnetilise väljatugevuse näiteid

Maa magnetväli on tugevusega umbes 40 µT (0,4 G). Kõige nõrgem on magnetväli galaktikatevahelises ruumis (0,1 nT) ja tugevaim neutrontähtede pinnal (üle 100 MT).^[10]. (vt Mõõtühikute detsimaaleesliited)

Berliini instituudis Physikalisch-Technischen Bundesanstalt on ajuvoolude ja südamesignaalide uurimiseks loodud spetsiaalne varjestatud ruum, kus magnetinduktsioon on vaid 1 nT. Florida instituudis National High Magnetic Field Laboratory on saavutatud seni tugevaim püsiv magnetväli 5 T.

Magnetvälja energia

Iga magnetväli sisaldab energiat. Energiatihedus $\rho _{\mathrm {m} }$ magnetvälja suvalises punktis vaakumis :

\rho _{\mathrm {m} }={\frac {1}{2}}BH={\frac {1}{2}}\mu _{0}H^{2}={\frac {B^{2}}{2\mu _{0}}},

kus $H$ on magnetvälja tugevus, $B$ on magnetiline induktsioon antud punktis ja $\mu _{0}$ on magnetiline konstant (vaakumi magnetiline läbitavus).

Näiteks vooluga pooli magnetvälja energia avaldub kujul

W={\frac {\Phi I}{2}}={\frac {LI^{2}}{2}},

kus $\Phi$ on pooli tekitatud magnetvoog, $L$ on pooli induktiivsus ja $I$ on pooli keerde läbiva voolu tugevus.

Magnetvälja jõujooned

Magneti jõujooned on esitatud rauapuru joondumisena

Magnetvälja jõujooned on kujutletavad või joonestatud jooned, mis määravad välja igas punktis magnetvälja (või magnetvoo) suuna. See ühtib jõujoone puutujaga selles punktis ja on suunatud välja lõunapooluse poole. Seega on väli suunatud sinnapoole, kuhu osutab proovimagneti (kompassi magnetnõela) põhjapoolus. Väljatugevus on võrdeline proovimagnetile mõjuva pöördemomendiga, kui see on oma stabiilsest asendist teatava nurga võrra ära pööratud. Magnetväli on seda tugevam, mida tihedamalt on väljajooni selles kohas.

Magnetostaatilises väljas ei ole võimalik eraldada üksikut poolust (monopoolust), nii nagu elektrostaatikas positiivset ja negatiivset poolust. Magnetvälja jõujoontel pole algust ega lõppu, nad sulguva näiteks läbi püsimagneti või suunduvad lõpmatusse, seetõttu on tegemist allikavaba ehk pööriselise väljaga.

Jõujoonte kulgu saab esile tuua magneti lähedale asetatud rauapuruga.^{[nb 5]}.

Vaata ka

Märkused

↑ Spinnmagnetmoment tekib, kui elementaarosakesel on nii laeng kui ka nullist suurem spinn
↑ Tehniliselt võttes on magnetväli pseudovektor; pseudovektorid on sarnased vektoritega, kuid sisaldavad ka pöördemomenti ja pöörlemiskiirust ning nad ei muutu, kui koordinaatsüsteemi käelisust muuta
↑ Tema "Epistola Petri Peregrini de Maricourt ad Sygerum de Foucaucourt Militem de Magnete", sageli lühendatud kujul "Epistola de magnete", on dateeritud 1269 AD
↑ Väljastpoolt on magnetlaengu dipooli väli identne vooluringi magnetväljaga, kui mõlemad on küllaltki väiksed. Seepärast erinevad need mudelid vaid magnetmaterjalisiseselt
↑ Rauapuru kasutatakse välja visualiseerimiseks, sest sellel on suur magnetiline läbitavus

Viited

↑ "Füüsika põhikursus" (David Halliday, Robert Resnick, Jearl Walker. Füüsika Põhikursus. 2. köide Tartu, Eesti Füüsika Selts, 2012 lk 736 ISBN 9789985907894
↑ Whittaker, E. T. (1951). A History of the Theories of Aether and Electricity. Dover Publications. Lk 34. ISBN 0-486-26126-3.
↑ Whittaker 1951, lk 56
↑ Whittaker 1951, lk 59
↑ Whittaker 1951, lk 64
↑ Whittaker 1951, lk 88
↑ Whittaker 1951, lk 222
↑ Whittaker 1951, lk 244
↑ Whittaker 1951, lk 422
↑ Kouveliotou, C.; Duncan, R. C.; Thompson, C. (February 2003). "Magnetars". Scientific American; Page 36

[1] Spinnmagnetmoment tekib, kui elementaarosakesel on nii laeng kui ka nullist suurem spinn

[3] Tehniliselt võttes on magnetväli pseudovektor; pseudovektorid on sarnased vektoritega, kuid sisaldavad ka pöördemomenti ja pöörlemiskiirust ning nad ei muutu, kui koordinaatsüsteemi käelisust muuta

[4] Tema "Epistola Petri Peregrini de Maricourt ad Sygerum de Foucaucourt Militem de Magnete", sageli lühendatud kujul "Epistola de magnete", on dateeritud 1269 AD

[10] Väljastpoolt on magnetlaengu dipooli väli identne vooluringi magnetväljaga, kui mõlemad on küllaltki väiksed. Seepärast erinevad need mudelid vaid magnetmaterjalisiseselt

[ex07-15] Rauapuru kasutatakse välja visualiseerimiseks, sest sellel on suur magnetiline läbitavus

[2] "Füüsika põhikursus" (David Halliday, Robert Resnick, Jearl Walker. Füüsika Põhikursus. 2. köide Tartu, Eesti Füüsika Selts, 2012 lk 736 ISBN 9789985907894

[Whittaker-5] Whittaker, E. T. (1951). A History of the Theories of Aether and Electricity. Dover Publications. Lk 34. ISBN 0-486-26126-3.

[Whittaker56-6] Whittaker 1951, lk 56

[Whittaker59-7] Whittaker 1951, lk 59

[Whittaker64-8] Whittaker 1951, lk 64

[Whittaker88-9] Whittaker 1951, lk 88

[Whittaker222-11] Whittaker 1951, lk 222

[Whittaker244-12] Whittaker 1951, lk 244

[Whittaker422-13] Whittaker 1951, lk 422

[14] Kouveliotou, C.; Duncan, R. C.; Thompson, C. (February 2003). "Magnetars". Scientific American; Page 36

[nb 1]

[1]

[nb 2]

[nb 3]

[2]

[3]

[4]

[5]

[6]

[nb 4]

[7]

[8]

[9]

[10]

[nb 5]