Biot'-Savarti seadus
Biot'-Savarti seadus (ka kujul Biot’-Savart’i-Laplace’i seadus) on elektromagnetismi seadus, mis kirjeldab statsionaarse (püsiva) elektrivoolu tekitatud magnetvälja. Biot'-Savarti seadusel on magnetostaatikas niisama oluline koht, nagu seda on Coulombi seadusel elektrostaatikas. Seadus toetub Ampère'i seadusele, mis määrab magnetväljas asuvale vooluga juhtmele mõjuva jõu, ja Gaussi magnetväljaseadusele .[1]
Seadus on nimetatud Jean-Baptiste Biot' ja Félix Savarti järgi, kes avastasid selle elektri- ja magnetnähtuste vahelise seose 1820. aastal, kui nad uurisid magnetvälju, mida tekitab elektrivool erineva kujuga juhtmetes.
Pierre-Simon Laplace analüüsis Biot' ja Savarti katseandmeid ning andis seadusele üldistatud kuju. Laplace näitas ka, et selle seaduse abil saab arvutada liikuva elektrilaengu magnetvälja.
Tänapäeval käsitletakse seda seadust enamasti järeldustena kahest Maxwelli magnetvälja võrrandist, et arvesse võtta ka välja ajalist muutumist.
Voolujuhi magnetväli[muuda | muuda lähteteksti]
Voolujuhi all mõeldakse elektrijuhti, mida läbib elektrivool. Voolujuhiks võib olla suvalise kujuga (sirge, kõver) juhe, ka juhtmekeerd või juhtmesilmus.

Biot'-Savarti seadus määrab voolu tekitatud magnetvälja (täpsemalt magnetiline induktsiooni ehk magnetvoo tiheduse) kohas , mis on arvutatav kui voolu elementaarlõikude tekitatud magnetväljade vektorsumma.[2] Matemaatiliselt on Biot'-Savarti seadus on väljendatav joonintegraalina üle vooluraja C:[3]
kus märgib vektorkorrutamist (vektorid on paksus kirjas)
- on voolu diferentsiaalne pikkusvektor, mille suund ühtib positiivse elektrilaengu liikumise suunaga;
- on vektor elemendist kuni punktini , kus arvutatakse magnetvälja;
- on magnetiline konstant.
Selle võrrandi saab esitada ka kujul
kus on vektori suunaline ühikvektor ja on vektori pikkus.

Pika sirge voolujuhi magnetväli[muuda | muuda lähteteksti]
Lõpmatult pika sirge voolujuhi iga punkti ümber kujuneb juhtme risttasandis magnetväli
kus
- on ristsunaline kaugus -teljest;
- on ühikvektor silinderkoordinaatide (ruumiliste polaarkoordinaatide) nurga suunas.
Seega paiknevad magnetinduktsiooni ühesugused väärtused voolujuhti kontsentriliselt ümbritsevatel silindrilistel pindadel ja magnetinduktsioon vektorkujul
Järelikult muutub magnetinduktsioon pöördvõrdeliselt kaugusega voolujuhist.
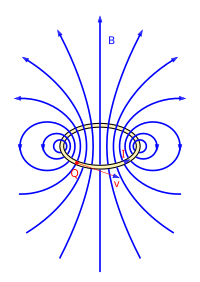
Voolusilmuse magnetväli[muuda | muuda lähteteksti]
Ringikujulise voolusilmuse (-kontuuri) ümber tekkiva välja magnetinduktsiooni vektori pikkuse saab määrata kontuuri sümmeetriatelje (z-telje) risttasandil võrrandiga
kus
- on xy-tasandil asetseva kontuuri raadius;
- on välja määramise punkti P kaugus xy-tasandist.
Kui punkti P kaugus voolukontuurist on palju suurem selle raadiusest, nõrgeneb väli z-teljel ligikaudu võrdeliselt kauguse kolmanda astmega.
Mitmekeerulise voolujuhi magnetväli[muuda | muuda lähteteksti]
Kui on tegemist mitmekeerulise voolujuhiga (pooliga), siis saab magnetvälja arvutada superpositsiooni põhimõttel:
Magnetväli jämedas voolujuhis[muuda | muuda lähteteksti]
Eeltoodud valemid sobivad, kui voolujuht on väga peenike .(ristlõige läheneb nullile). Kui elektrijuht on teatud jämedusega, siis pideva voolujaotuse korral kombineeritakse voolutiheduse joonintegraal piki juhti pindintegraaliga ja inegreritakse üle kogu juhtme ruumala V:
või väljendatuna ühikvektori kaudu:
kus on ruumiosa ja on voolutiheduse vektor selles ruumiosas (SI-süsteemis on ühikuks A/m2).
Konstantsel kiirusel liikuva punktlaengu elektri- ja magnetväli[muuda | muuda lähteteksti]
Kui punktlaenguga q osake liigub konstantse kiirusega v, väljendavad elektrivälja ja magnetvälja Maxwelli võrrandid[4]:
- või
kus on ühikvektor, mis on osakese algsest asendist suunatud punkti, kus välja määratakse, ning θ on nurk ja vahel.
Kui v2 ≪ c2, siis saab elektrivälja ja magnetvälja avaldada lihtsustud kujul:
Neid võrrandeid nimetatakse Biot'-Savarti seaduseks punktlaengu jaoks,[5] mis tuleneb nende sarnasusest eelnevalt esitatud Biot'-Savarti võrranditega. Need võrrandid tuletas esimesena Oliver Heaviside 1888. aastal.
Biot'-Savarti seadus, Ampère'i seadus ja Gaussi seadus magnetvälja kohta[muuda | muuda lähteteksti]
Magnetostaatikas magnetinduktsioon , mis on leitud Biot'-Savarti seaduse abil, rahuldab alati Gaussi seadust magnetvälja kohta ja Ampère'i seadust.[6]
Tõestus[6] Kui Biot'-Savarti seaduse võrrandis teha asendus
ja kasutada rootorite vektorkorrutist ning teadmist, et J ei sõltu -ist, saab võrrandi kirjutada kujul[6]
Kuna rootori divergents on alati null, siis see sätestab Gaussi seaduse magnetväljade kohta. Korrutades mõlemad pooled rootoriga, siis on tulemuseks[6]
Viimaks, viies sisse seosed[6]
(δ on Dirac'i deltafunktsioon), kasutades asjaolu, et divergents on null (eeldusel, et tegemist on magnetostaatikaga) ja teostades ositi integreerimise, siis tulemuseks on[6]
See on Ampère'i seadus. (Kuna eeldati, et tegemist on magnetostaatikaga, siis .)
Mittemagnetostaatilises olukorras Biot'-Savarti seadus enam ei kehti, aga Gaussi seadus magnetvälja kohta ja Ampère'i seadus kehtivad.
Kui magnetostaatika tingimused ei kehti, siis tuleks Biot'-Savarti seadus asendada Jefimenko võrranditega.[7] Koos pidevusvõrrandiga (ingl continuity equation) on Jefimenko võrrandid ekvivalentsed Maxwelli võrranditega.
Rakendused aerodünaamikas[muuda | muuda lähteteksti]
Biot'-Savarti seadus leiab kasutust ka aerodünaamikas, et leida kiirust, mida põhjustavad õhupöörised. Aerodünaamika rakendustes on pööriselise välja ja voolu rollid vahetatud, võrreldes elektromagnetilise rakendusega.
Maxwelli järgi[8] on magnetvälja tugevus H otseselt võrdsustatud pööriselisusega.
Vaata ka[muuda | muuda lähteteksti]
Viited[muuda | muuda lähteteksti]
- ↑ Jackson, John David (1999). Classical Electrodynamics (kolmas ed.). New York: Wiley. Peatükk 5. ISBN 0-471-30932-X.
{{cite book}}: eiran tundmatut parameetrit|nopp=, kasuta parameetrit (|no-pp=) (juhend) - ↑ Saveljev, Igor (1978). Füüsika üldkursus II. Tallinn: Valgus. lk 90.
{{cite book}}: eiran tundmatut parameetrit|nopp=, kasuta parameetrit (|no-pp=) (juhend) - ↑ Grant, I.S., Phillips, W.R. (1991). Electromagnetism (teine ed.). Manchester: John Wiley & Sons. ISBN 978-0-471-92712-9.
{{cite book}}: eiran tundmatut parameetrit|nopp=, kasuta parameetrit (|no-pp=) (juhend)CS1 hooldus: mitu nime: autorite loend (link) - ↑ Griffiths, David J. (1998). Introduction to Electrodynamics (kolmas ed.). New Jersey: Prentice Hall. ISBN 0-13-805326-X.
{{cite book}}: eiran tundmatut parameetrit|nopp=, kasuta parameetrit (|no-pp=) (juhend) - ↑ "Arhiveeritud koopia". Originaali arhiivikoopia seisuga 19.06.2009. Vaadatud 19.01.2019.
- ↑ 6,0 6,1 6,2 6,3 6,4 6,5 Jackson, John David (1999). Classical Electrodynamics (kolmas ed.). New York: Wiley. leheküljed 178-179. ISBN 0-471-30932-X.
{{cite book}}: eiran tundmatut parameetrit|nopp=, kasuta parameetrit (|no-pp=) (juhend). - ↑ de Melo e Souza, R.; Cougo-Pinto, M. V.; Farina, C. (2009). "Multipole radiation fields from the Jefimenko equation for the magnetic field and the Panofsky-Phillips equation for the electric field". American Journal of Physics. 77 (1): 67–72. DOI:10.1119/1.2990666. Originaali arhiivikoopia seisuga 12. märts 2022. Vaadatud 20. jaanuaril 2019.
- ↑ Maxwell, J. C. "On Physical Lines of Force" (PDF). Wikimedia commons. Vaadatud 19.01.2018.













































