Magnetiline monopoolus
Magnetiline monopoolus on hüpoteetiline elementaarosake osakestefüüsikas, mis kujutab endast ühe poolusega eraldiseisvat magnetit (põhjapoolus ilma lõunapooluseta või vastupidi).[1][2] Täpsemalt sõnastades võib öelda, et monopoolusel on teatav "magnetiline kogulaeng". Huvi taolise osakese vastu lähtub osakestefüüsika teooriatest, peamiselt suure ühenduse ja superstringiteooriatest, mis ennustavad selle olemasolu.[3][4]
Elektro- ning varrasmagnetites esinev magnetism ei ole seotud magnetiliste monopoolustega. Veelgi enam, tänapäevani ei ole ühtegi määrava kaaluga eksperimentaalset tõestust monopooluste eksistentsist.
Leidub kondensaine süsteeme, kus esineb vastastikmõjus olevaid magnetmonopooluselaadseid kvaasiosakesi[5] või milles avalduvad nähtused on matemaatiliselt analoogilised magnetiliste monopoolustega.[6]
Ajalooline taust
[muuda | muuda lähteteksti]Enne 20. sajandit
[muuda | muuda lähteteksti]Mitmed varajased teadlased põhjendasid magnetiitide magnetvälja olemasolu kahe eri liiki "magnetilise vedelikuga" (effluvia). Ühes otsas oli põhjapooluse-vedelik ning teises lõunapoolusevedelik, mis tõukusid ning tõmbusid analoogselt positiivsete ja negatiivsete elektrilaengutega.[7][8] 19. sajandil toimunud areng elektromagnetismi teoorias viisid arusaamani, et magnetiitide magnetismi kirjeldab õigesti Ampère'i seadus, mitte aga magnetilised monopoolus-vedelikud. Gaussi magnetismi seadus, üks Maxwelli võrranditest, iseloomustab matemaatiliselt magnet-monopooluste puudumist. Sellele vaatamata näitas 1894. aastal Pierre Curie, et taolised monopoolused võivad põhimõtteliselt eksisteerida,[9] kuigi neid ei olnud selleks ajaks katseliselt vaadeldud.
20. sajand
[muuda | muuda lähteteksti]Magnetlaengu kvantmehaaniline käsitlus sai alguse füüsik Paul A. M. Diraci 1931. aastal ilmunud artikliga,[10] milles Dirac näitas, et kui universumis peaks leiduma mõnigi magnetiline monopoolus, siis peab kogu olemasolev elektrilaeng olema kvantiseeritud.[11] Elektrilaeng on tõepoolest kvantiseeritud, mis on küll kooskõlas monopooluste olemasoluga, kuid ei ole piisav selle tõestamiseks.[11] Pärast Diraci artikli avaldamist on läbi viidud mitmeid süstemaatilisi magnetiliste monopooluste otsinguid. 1975.[12] ja 1982.[13] aastal sooritatud eksperimentides leiti sündmusi, mida tõlgendati monopoolustena, kuid tänapäeval ei peeta neid piisavalt usaldusväärseteks.[14] Seega monopooluste võimalik olemasolu on tänaseni lahtine. Edasine areng teoreetilise osakestefüüsika vallas, eriti areng suure ühenduse ja kvantgravitatsiooni teooriates on toonud esile veelgi kaalukamaid argumente magnetiliste monopooluste olemasolu kasuks. Stringiteooriat uuriv Joseph Polchinski on monopooluste eksistentsi iseloomustanud kui "üht kindlaimat kihlvedu, mida võib seninägemata füüsika kohta teha."[15] Toodud teooriad ei ole eksperimentaalsete tulemustega tingimata vastuolus. Mõne teooria kohaselt on magnetiliste monopooluste leidmine ebatõenäoline, kuna monopooluse mass on liialt suur tema tekitamiseks osakestekiirendis ning samuti eksistents universumis liiga haruldane, et neid osakeste detektoris arvestatava tõenäosusega registreerida.[15] Mõnedes kondensaine süsteemides luuakse struktuure, mis paistavad vähemalt pinnapealselt magnetiliste monopooluste sarnastena – neid nimetatakse vootorudeks (flux tube). Vootoru otsad moodustavad monopoolused, kuid kuna nende nihutamine on võimalik teineteisest sõltumatult, võib neid tinglikult pidada sõltumatuteks magnetilisteks monopoolus-kvaasiosakesteks. Alates 2009. aastast on mitmed populaarteaduslikud väljaanded[16] [17] taolisi süsteeme ekslikult kirjeldanud kui kauaoodatud magnetiliste monopooluste avastamist, kuid tegu on kahe vaid pinnapealselt võrreldava nähtusega.[18][19] Sellele vaatamata on taoliste kondensaine süsteemide näol tegemist aktiivse uurimissuunaga.
Poolused ja magnetism tavapärases aines
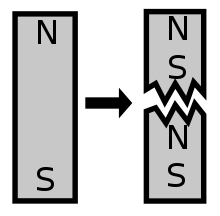
[muuda | muuda lähteteksti]Kogu ainel, mida seni oleme vaadelnud – hõlmates kõiki aatomeid perioodilisussüsteemis ja kõiki osakesi standardmudelis – puudub igasugune magnetmonopoolus-laeng. Tavapärasel magnetismi ja magnetite nähtusel ei ole monopoolustega midagi pistmist. Selle asemel on tavaaines magnetismi tekkeks kaks allikat: esiteks tekivad magnetväljad elektrivoolust, vastavalt Ampère'i seadusele ning teiseks on mitmetel elementaarosakestel teatav loomupärane magnetmoment (näiteks elektroni spinni põhjustatud elektroni magnetiline dipoolmoment). Matemaatiliselt kirjeldatakse magnetvälja tihtipeale multipoolarendusena, mis esitab välja mitme komponendi summana. Arenduse esimest liiget nimetatakse monopool-liikmeks, teist dipool-liikmeks ning edasi kvadrupool- ja oktapool-liikmed jne. Kui elektrivälja multipoolarenduses võivad esineda kõik need liikmed, siis magnetvälja korral on monopool-liige alati null (tavaaine korral). Kui magnetiline monopoolus tõepoolest eksisteerib, siis tema tekitatava magnetvälja multipoolarenduse monopool-liige oleks nullist erinev. Magnetdipooli magnetvälja kirjeldab hea täpsusega multipoolarenduse dipool-liige. Nagu dipooli nimi viitab, on sellel kaks poolust – ühes otsas põhja- ja teises lõunapoolus – mis on analoogne elektridipooliga (ühes otsas positiivne ning teises negatiivne elektrilaeng). Sellele vaatamata on magnetiline ja elektriline dipool olemuslikult erinevad. Tavaainest elektridipooli positiivse laengu moodustavad prootonid ja negatiivse elektronid, samas kui magnetdipooli kaks poolust ei moodustu kahtedest eri liiki osakestest. Mõlemad magnetpoolused tekivad koos ja samaaegselt ning on põhjustatud kõigist magnetis esinevatest voolust ja sisemistest momentidest tingitud nähtustest. Siit järeldub, et magnetdipooli poolused on alati võrdse ja vastasmärgilise väljatugevusega ning neid on võimatu teineteisest eraldada.
Maxwelli võrrandid
[muuda | muuda lähteteksti]Maxwelli võrrandid elektromagnetismis seovad omavahel elektri- ja magnetvälja. Tavapärasel kujul kirjapandult on võrrandeis esindatud küll elektrilaengud, kuid puuduvad magnetlaengud. Kui see välja jätta, on võrrandid elektri- ja magnetväljade vahetamise suhtes sümmeetrilised.[20] Veelgi enam, Maxwelli võrrandeid saab kirja panna ka juhu jaoks, kus kõik laengud (seega ka elektrivoolud) on nullid. Sel viisil tuletatakse elektromagnetlaine võrrand. Täielikult sümmeetrilisi Maxwelli võrrandeid on võimalik esitada ka viisil, mis lubab magnetlaengute olemasolu.[21] Lisades muutuja , mis iseloomustab taoliste laengute tihedust, tekib võrranditesse ka magnetvoolutiheduse muutuja, . Kui magnetlaenguid ei eksisteeri (või kui neid vaadeldavas ruumipiirkonnas parasjagu ei ole), siis vastavad uued muutujad on kõik nullid ning võrrandid taanduvad tavapärasele kujule.[22][23]
CGS-süsteemi ühikutes
[muuda | muuda lähteteksti]Täiendatud Maxwelli võrrandid Gaussi CGS-süsteemi ühikutes esitatuna on järgmised.[24]
Nimi Ilma monopoolusteta Monopoolustega Gaussi lause Gaussi lause magnetvälja kohta Faraday seadus Ampère'i seadus (Maxwelli täiendusega) Lorentzi jõud[24][25]
Neis võrrandeis on magnetlaengu tihedus, magnetvoolu tihedus ja katseosakese magnetlaeng, mis kõik on defineeritud analoogiliselt vastavate elektrilaengu ja -voolu suurustega. on osakese kiirus ning on valguse kiirus vaakumis. Kõik ülejäänud esitatud suurused on toodud Maxwelli võrrandite lehel.
SI-süsteemi ühikutes
[muuda | muuda lähteteksti]SI-süsteemi ühikutes on magnetlaengu kirjeldamiseks kasutusel kaks vastuolulist ühikut: veeber (Wb) ja amper meeter (A m). Kuna 1 Wb = 1 H A = (H m−1) (A m), siis teisendus ühest esitusviisist teise on (Wb) = μ0 (A m). Sel juhul omandavad Maxwelli võrrandid järgmise kuju.[26]
Nimi Ilma monopoolusteta Veeberi esitusviis Amper meeter esitusviis Gaussi lause Gaussi lause magnetvälja kohta Faraday seadus Ampère'i seadus (Maxwelli täiendusega) Lorentzi jõud
Tensoresitus
[muuda | muuda lähteteksti]Maxwelli võrrandite esitamine tensorkujul näitab selgelt Lorentzi kovariantsust. Üldistatud võrrandid avalduvad järgmiselt.[27][28]
Maxwelli võrrandid CGS ühikutes SI ühikutes (Wb) SI ühikutes (A m) Faraday-Gaussi teoreem Ampère-Gaussi teoreem Lorentzi jõud
kus
- on elektromagnetvälja tensor, tähistab Hodge'i duaalsust (seega on -i duaalne tensor),
- ja on elektrilaenguga ja magnetlaenguga osakese kiiruse ja impulsi nelivektorid,
- = (,) on elektrilaengu nelivektor ja = (,) magnetlaengu nelivektor.
Kui osakesel on vaid elektrilaeng, siis saab välja kirjeldada elektrivälja potentsiaali nelivektoriga, vastavalt klassikalise elektromagnetismi kovariantsele formuleeringule:
See võrrand on aga ebapiisav osakese jaoks, millel on nii elektri- kui ka magnetlaeng. Sel juhul tuleb lisada üks lisapotentsiaali kirjeldav liige .[29][30]
Seda väljavõrrandit nimetatakse üldiselt Cabibbo-Ferrari seoseks, kuigi Shanmugadhasan tuli sellega varem välja.[30] Suurus εαβγδ on Levi-Civita sümbol, mille indekseid tuleb käsitleda vastavalt Einsteini summeerimisreeglile.
Duaalne teisendus
[muuda | muuda lähteteksti]Üldisel kujul Maxwelli võrranditel on teatav sümmeetria, mida nimetatakse duaalseks teisenemiseks. Valides suvalise reaalse nurga ξ, saab vastavalt allolevatele seostele muuta samaaegselt välju ja laenguid (CGS-süsteemi ühikutes).[31]
Laengud ja voolud Väljad
kus priimiga tähistatud suurused vastavad laengutele ja väljadele enne teisendust ja ilma priimita suurused pärast teisendust. Teisendatud väljad ja laengud vastavad ikka Maxwelli võrranditele. Vaadeldav maatriks on kahemõõtmeline pöördmaatriks.
Duaalse teisenduse tõttu ei ole võimalik vaid osakese käitumist jälgides ning seda Maxwelli võrranditega võrreldes määrata, et osakesel on eranditult elektrilaeng või magnetlaeng või mõlemad. Näiteks on vaid kokkuleppeline, mitte aga Maxwelli võrrandite eeldus, et elektronidel on elektrilaeng, kuid puudub magnetlaeng; Pärast ξ = π/2 teisendust oleks olukord vastupidine. Võtmelise tähtsusega empiiriliseks faktiks on see, et kõikidel seni vaadeldud osakestel on magnet-ja elektrilaengu suhe sama.[31] Duaalsete teisendustega saab laengute suhte viia suvalisele väärtusele, kuid see suhe on alati kõigi osakeste jaoks võrdne. Siit järeldub, et magnetlaengu ja elektrilaengu suhte saab vastavalt valitud teisendusega viia nulliks, nii et kõigil osakestel puudub magnetlaeng. See valikuvabadus on kaasaegsete elektri ja magnetismi definitsioonide alustalaks.[31]
Diraci kvantiseerimine
[muuda | muuda lähteteksti]Üks Kvantmehaanika (KM) suurimaid arenguid tulenes Paul Diraci tööst elektromagnetismi relativistliku kvantteooria väljaarendamisel. Varem sisestati elektrilaengu olemasolu KM võrranditesse ilma matemaatiliste põhjendusteta, kuid Dirac näitas 1931 aastal, et diskreetne laeng tuleneb KM-st küllaltki loomulikult. See tähendab, et magnetlaengud saavad eksisteerida ka Maxwelli võrrandite muutmata kujul.
Võime vaadelda näiteks süsteemi, mis koosneb üksikust statsionaarsest elektrimonopoolusest (nt elektron) ning üksikust statsionaarsest magnetmonopoolusest. Klassikalise füüsika järgi on neid kahte ümbritseva elektromagnetvälja impulsitihedus esitatav Poyntingi vektoriga, ning välja kogu impulsimoment on proportsionaalne korrutisega ning sõltumatu pooluste vahelisest kaugusest.
Kvantmehaanika järgi on aga impulsimoment kvantiseeritud kordselt. Seega peab ka korrutis olema kvantiseeritud. Järeldub, et kui vaid ükski magnetiline monopoolus universumis eksisteerib, ning Maxwelli võrrandid kehtivad, siis peavad kõik elektrilaengud olema kvantiseeritud.
Mis ühikutena oleks magnetlaeng kvantiseeritud? Kuigi oleks võimalik integreerida üle kogu ruumi, et leida eeltoodu näitel kogu impulsimoment, kasutad Dirac teist lähenemist. Ta uuris magnetlaenguga punktobjekti, mille magnetvälja kirjeldab /², kus väli on raadiuse suunas. Kuna magnetvälja B divergents on null kõikjal peale magnetmonopooluse asukoha r = 0, saab vektorpotentsiaali defineerida nii, et vektorpotentsiaali A rootor on võrdne magnetväljaga B
Kuna aga magnetvälja divergents on asukohas r = 0 võrdeline Diraci deltafunktsiooniga, ei ole vektorpotentsiaali võimalik kõikjal täpselt defineerida. Selleks tuleb vektorpotentsiaal jagada nii, et sõnastame "põhjapoolkera" (poolruum z > 0 osakese kohal) ja "lõunapoolkera" jaoks eraldi funktsioonid, mis kattuvad ekvaatoril (tasand z = 0 läbi osakese) ning mis erinevad teineteisest kalibratsiooniteisenduse võrra. Elektriliselt laetud osakese (proovilaengu) tiireldes ümber ekvaatori muutub osakese lainefunktsiooni faas, sarnaselt Aharonovi-Bohmi efektiga. Faas on võrdeline proovilaengu elektrilaenguga ja allika magnetlaenguga . Algselt kaalus Dirac elektroni, mille lainefunktsiooni kirjeldab Diraci võrrand.
Pärast täistiiru tegemist ümber ekvaatori naaseb elektron samasse kohta, kust alustas, mistõttu jääb tema lainefunktsiooni eiφ faas φ muutumatuks. Järeldub, et lainefunktsioonile liidetav faas φ peab olema 2π-kordne:
Ühikud Tingimus Gaussi CGS ühikud SI ühikud (Veeberi esitusviis)[32] SI ühikud (Amper meeter esitusviis)
kus on vaakumi dielektriline läbitavus, = / on Plancki nurkkonstant, on valguse kiirus ning täisarvude hulk.
Seda tuntakse Diraci kvantiseerimise tingimusena. Magnetilise monopooluse hüpoteetiline olemasolu viitab, et elektrilaeng on teatud viisil kvantiseeritud. Samuti, elektrilaengute olemasolu viitab, et monopooluste magnetlaengud, kui nad eksisteerivad, peavad olema kvantiseeritud ühikutes, mis on võrdelised elementaarlaengu pöördväärtusega.
Tollal ei olnud selge, kas taoline osake eksisteerib või kas selleks üldse on vajadust. Oli väga võimalik, et ilmneb mõni teine teooria, mis kirjeldab laengu kvantiseeritust, vajamata selleks magnetmonopooluste olemasolu. Sellegipoolest ei ole seni ilmnenud ühtegi teist laialdaselt aktsepteeritud selgitust laengu kvantiseerituse kohta.
"Lõunapoolusel" on vektorpotentsiaal pidev kõikjal peale poollõpmatu joone, mis lähtub allikast ning on "põhjapooluse" sihis. Seda poollõpmatut joont nimetatakse Diraci stringiks ning selle mõju lainefunktsioonile on analoogne solenoidi mõjule Aharonov-Bohmi efektis. Kvantiseeritus tuleneb nõudest, et Diraci stringi ümbritsevad faasid on triviaalsed, mis tähendab, et Diraci string peab olema mittefüüsikaline. Diraci string on vaid kasutatava koordinaadistiku anomaalia ning seda ei tohiks tõsiselt võtta.
Diraci monopoolus on Maxwelli võrrandite singulaarne lahend (kuna selle tingimuseks on maailmajoone eraldamine aegruumist). Keerukamates teooriates on see asendatud mõne sileda lahendiga nagu 't Hoofti-Poljakovi monopoolus.
Suure ühenduse teooriad
[muuda | muuda lähteteksti]1970. aastate alguses tehti suuri samme kvantväljateoorias ja kalibratsiooniteoorias, elektronõrga teooria ja tugeva vastastikmõju arendamise käigus, mille tulemusel asusid paljud teoreetikud proovima neid ühte teooriasse kombineerida – suure ühenduse teooria (SÜT). Pakuti mitmeid SÜT-sid, enamik millest viitasid reaalse magnetilise monopooluse olemasolule. Täpsemalt, need teooriad ennustasid hulka osakesi, mida nimetati düüoniteks ning mille kõige algsem olek on magnetmonopoolus.
Suurem enamus kvantväljateooriates esinevatest osakestest on ebastabiilsed ning lagunevad teisteks osakesteks mitmetel jäävusseadustega kooskõlas olevatel viisidel. Osakesed on stabiilsed, kui neil puudub viis jäävusseadusi rikkumata veel kergemateks osakesteks laguneda. Näiteks elektroni puhul on nii leptonarv kui elektrilaeng võrdsed ühega ning puuduvad veel kergemad osakesed, mille jaoks need suurused on jäävad. Samas näiteks müüon, mis on olemuselt kui raske elektron, võib laguneda elektroniks ja kaheks energiakvandiks ning on seetõttu ebastabiilne.
SÜT-des esinevad düüonid on samuti stabiilsed, kuid seda teistel põhjustel. Düüonite teke oli eeldatavasti varajase universumi keskkonna "kinnistumise" ("freeze out") – sümmeetria rikkumise – kõrvalnähtus. Selle stsenaariumi järgi tekivad düüonid vaakumi teatud konfiguratsiooni korral mingis ruumipiirkonnas, vastavuses algse Diraci teooriaga. Nad on stabiilsed, kuna puuduvad veel lihtsamad topoloogilised olekud, kuhu neil oleks võimalik laguneda.
Taolise vaakumi konfiguratsiooni ruumimõõdet nimetatakse süsteemi korrelatsioonipikkuseks, mis ei saa olla suurem, kui põhjuslikkus lubab. Seetõttu peab magnetiliste monopooluste loomiseks vajalik korrelatsioonipikkus olema vähemalt sama suur, kui paisuva universumi meetrika määratud horisondi mõõtmed. Selle loogika järgi peaks eksisteerima iga horisondiruumi kohta vähemalt üks magnetiline monopoolus, nagu see oli siis kui sümmeetria rikkumine aset leidis.
Suurele Paugule vahetult järgnevate sündmuste kosmoloogilised mudelid sisaldavad teatud eeldusi taolise horisondiruumi kohta. Neist eeldustest lähtuvalt on võimalik oletada monopooluste ruumtihedust. Algsed mudelid näitasid tohutusuurt monopooluste hulka, mis oli selges vastuolus katsetest saadud tulemustega.[33][34] Seda nimetati "monopooluse probleemiks," mille hiljem laialdaselt aktsepteeritud lahend ei saabunud mitte seetõttu, et muudeti osakestefüüsika arusaama monopoolustest, vaid kuna kohandati algseid kosmoloogilisi mudeleid, millest saame hinnata monopooluste tänapäevast esinemissagedust. Täpsemalt, nüüdisaegsemad kosmoloogilise inflatsiooni teooriad vähendavad magnetiliste monopooluste eeldatavat esinemissagedust sel määral, et nende senine eksperimentaalse registreerimise ebaedu ei ole imekspandav.[35] Taolist lahendust "monopooluse probleemile" peetakse inflatsiooniteooria võiduks. (Mõistagi, tegu on edulooga vaid juhul, kui osakestefüüsika eeldus magnetilisest monopoolusest peab paika.[36]) Neil põhjustel sai monopoolustest 1970. ja 1980. aastatel suur uurimisvaldkond, paralleelselt teiste SÜT ennustustega, mille vaatlemine võiks olla ka realistlik, nagu näiteks prootoni lagunemine kergemateks subatomaarseteks osakesteks.
Mitmete teiste SÜT ennustatud osakeste vaatlemine on aga väljaspool teaduse kaasaegset eksperimentaalset võimekust. Näiteks eeldatakse, et elektronõrga ja tugeva vastasmõju omavahelist interaktsiooni vahendab suur osakesteklass, mida nimetatakse X- ja Y-bosoniteks, kuid need osakesed on äärmiselt suure massiga ning nende vaatlemine kindlalt väljaspool ka kõige võimsamate osakestekiirendite võimekust.
Magnetiliste monopooluste otsingud
[muuda | muuda lähteteksti]Monopooluste vaatlemiseks on läbi viidud mitmeid eksperimente. Üks lihtsamaid neist kujutab endast ülijuhtiva traadi abil ka kõige pisemate magnetiliste allikate otsimist. Seda nimetatakse ülijuhtivaks kvantinterferentsseadeks ehk skviidiks (SQUID). Arvestades monopooluste eeldatavat ruumtihedust, võiksid laborilauale mahtuvad skviidid registreerida keskmiselt ühe sündmuse aastas. Kuigi on vaadeldud ärevusttekitavaid sündmusi, eriti Blas Cabrera poolt 14. veebruaril 1982 registreeritud sündmus (nn valentinipäeva monopoolus[37]), ei ole siiani õnnestunud leida magnetpooluste olemasolu kohta reprodutseeritavaid tõendeid. Taoliste sündmuste puudumine on seadnud monopooluste hulga ligikaudseks piiriks ühe monopooluse 1029 nukleoni kohta.
1975. aastal P. Buford Price'i juhitud tiimi eksperimendi järel kuulutati liikuva magnetilise monopooluse avastamist kosmilisest kiirgusest.[12] Hiljem aga võttis Price oma väite tagasi ning võimaliku alternatiivse selgituse käis välja Luis W. Alvarez.[38] Alvarez demonstreeris oma artiklis, et registreeritud kosmilise kiirguse sündmuse trajektoori, mille väidetavalt jättis magnetiline monopoolus, võib reprodutseerida plaatina tuumaga, mis laguneb esmalt osmiumiks ning seejärel tantaaliks.
Osa eksperimente lähtuvad teadmisest, et monopoolused, nagu ka kõik elektriliselt laetud osakesed on vastastikmõjus footonitega. Footonite vahetamisega seotud eksperimentides osakestekiirendites peaks põhimõtteliselt tekkima arvestatav hulk monopoolused, mida siis detekteeritakse mõõtes nende mõju footonite hajumisele. Taolises eksperimendis osakese tekitamise tõenäosus on võrdeline tema massiga – suurema massiga osakene tekib väiksema tõenäosusega – seega saab eksperimentide tulemustest lähtuvalt seada võimalikud piirid magnetiliste monopooluste massile. Üks viimaseid eksperimente näitas, et alla 600 GeV/c² massiga monopoolusi ei eksisteeri. Massi ülemise piiri seab universum – kui monopooluse mass oleks suurem kui 1017 GeV/c², siis oleks universum kollapseerunud.
LHC-s on üles seatud MoEDAL-i eksperiment, mille eesmärgiks on otsida magnetilisi monopoolusi ja suuri supersümmeetrilisi osakesi, kasutades selleks mitmeid LHCb eksperimendi VELO detektorit ümbritsevatele seintele kinnitatud erilisi plastikkihte. Otsitavad osakesed kahjustavad oma teel neid kihte, jättes seeläbi mitmeid analüüsitavaid jälgesid.
Vene astrofüüsik Igor Novikov viitab võimalusele, et magnetilistest monopoolustest moodustuvad makroskoopiliste mustade aukude magnetväljad, mis on seeläbi Einstein–Roseni silla alguseks.[39]
"Monopoolused" kondensainesüsteemides
[muuda | muuda lähteteksti]Alates aastast 2003 on mitmed kondensainefüüsika töörühmad kasutanud "magnetilise monopooluse" mõistet kirjeldamaks üht teist põhimõtteliselt erinevat nähtust.[18][19]
Tõelise monopooluse näol oleks tegemist uue elementaarosakesega, mis rikuks Gaussi lauset magnetväljade kohta . Sedalaadi osakest, mis aitaks selgitada 1931. aastal Paul Diraci sõnastatud laengu kvantiseeritust,[40] ei ole tänapäevani vaadeldud.. Sedalaadi osakest, mis aitaks selgitada 1931. aastal Paul Diraci sõnastatud laengu kvantiseeritust,[40] ei ole tänapäevani vaadeldud.
Kondensaine töörühmade uuritavatel monopoolustel need omadused puuduvad. Tegu ei ole uue elementaarosakesega, vaid pigem igapäevaste osakeste (prootonid, neutronid, elektronid, footonid) koosmõjul esineva nähtusega. Teisisõnu, tegemist on kvaasiosakestega. Nad ei ole magnetvälja allikaks (ei riku seadust), vaid hoopis allikaks teistele väljadele, nagu H-väli[5] või B*-väli, mis on seotud ülivoolava vedeliku kvantiseeritud keeristega.[6] Neil puudub arvestatav seos Suure Ühenduse teooriatega või ka osakestefüüsika muude aspektidega ega aita selgitada laengu kvantiseeritust – välja arvatud see, et analoogiliste olukordade uurimise abil on võimalik kinnitada matemaatiliste alustalade õigsust.[41]
Kondensainefüüsikast on mitmeid näiteid, kus osakeste kollektiivsete mõjude tulemusel ilmnevad magnetmonopooluste-sarnased nähtused,[17][42][43][44] peamiselt spinn-jää materjalides.[5][45] Kuigi neid ei tohi kindlasti segamini ajada hüpoteetiliselt vaakumis eksisteerivate magnetmonopoolus-osakestega, on neil sellegipoolest sarnaseid omadusi ja neid võib uurida sarnaste võtete abil.
Mitmed uurijad kasutavad monopoolus-kvaasiosakeste spinn-jääs käsitlemisele mõeldes terminit magnekter (magnet-elekter, ingl k magnetricity),[45][46] analoogselt sõnaga "elekter."
Üks näide taoliste kvaasiosakeste uurimusest on Science ajakirjas aastal 2009 avaldatud artikkel, milles J. Morris ja A. Tennant Helmholtz-Zentrum Berlin für Materialien und Energie uurimuskeskusest, S. Grigera Vedelike ja Bioloogiliste Süsteemide Füüsika Instituudist Argentinas ning teised teadlased Dresdeni Tehnikaülikoolist, Saint Andrewsi Ülikoolist ja Oxfordi Ülikoolist kirjeldasid monopooluselaadsete kvaasiosakeste vaatlemist. Katse käigus viidi düsproosium-titanaadist spinn-jää kristall temperatuurini 0,6–2,0 kelvinit. Neutronite hajumise jälgimisel täheldati, et magnetmomendid liituvad tubulaarsete kimpudena, mis meenutavad Diraci stringe. Iga taolise torukese otsa moodustub kristallograafiline defekt, mida ümbritsev magnetväli meenutab magnetilise monopooluse välja. Välise magnetvälja abil rikuti süsteemi sümmeetria, mis võimaldas uurijatel varieerida kimpude tihedust ja orientatsiooni. Töös uuriti ka kvaasiosakeste, mida võis vaadelda kui pilve või teatud gaasina, mõju süsteemi soojusmahtuvusele.[16] [47]
Selle uurimuse eest saadi 2012 aastal auhind Europhysics Prize for condensed matter physics
Teiseks näiteks on 2011 veebruaris Nature Physics ajakirjas ilmunud artikkel, mis kirjeldab pikema elueaga magnetmonopoolus-kvaasiosakeste voolude teket ja mõõtmist spinn-jääs. 0.36 K temperatuuril düsproosiumtitanaadist kristallile rakendati impulssrežiimis magnetväli, millega saavutati relakseeruv magnetvool, mis säilis mitmeid minuteid. Vool mõõdeti solenoidis indutseeritud elektromotoorjõu kaudu ning selle kvantitatiivseks kirjeldamiseks kasutati Onsageri-Wieni laengukandjate dislokatsiooni ja rekombinatsiooni mehhanismile alluvate punktlaengute keemilis-kineetilist mudelit. Seeläbi tuletati spinn-jääs monopooluste liikumisi iseloomustavad mikroskoopilised parameetrid ning fikseeriti vabade ja seotud magnetlaengute rollid.[46]
Ülivoolavates vedelikes avaldub B*-väli, mida seostatakse ülivoolates vedelikes tekkivate kvantiseeritud keeristega (superfluid vorticity) ning mis on matemaatiliselt analoogilised magnetväljaga B. Selle sarnasuse tõttu nimetatakse B*-välja "sünteetiliseks magnetväljaks." 2014 jaanuaris anti teada, et spiinorruumi Bose-Einsteini kondensaadis loodi ja uuriti B*-välja monopooluselisi kvaasiosakesi.[6] Selle näol on tegemist esimese juhuga, kus magnetilist monopoolust vaadeldi kvantväljateooriaga kooskõlalises süsteemis.[41]
Täiendavad kirjeldused osakestefüüsikas
[muuda | muuda lähteteksti]Füüsikas viitab "magnetilise monopooluse" mõiste üldiselt Yangi-Millsi potentsiaalile A ning Higgsi väljale ϕ, mille liikumisvõrrandid määrab Yangi-Millsi mõjufunktsioon
Matemaatikas tähistab see mõiste üldiselt ülaltoodud võrrandi statsionaarset lahendit Bogomolny–Parasad–Sommerfeldi piiril λ → ϕ, mille kaudu realiseerub järgneva funktsionaali globaalne miinimum:
See tähendab, et tegu on vektorkimbu ühendusega (connection) A printsipaal-G-ühendusel hulgas 3 ning Lie algebra vastava kõrvalkimbu lõiguga ϕ. Kõver FA ja kovariantne tuletis DAϕ peavad rahuldama Bogomolny võrrandeid
Alates 1980. aastatest on magnetiliste monopooluste teooria matemaatiliste edasiarenduste aluseks tihtipeale olnud füüsikalise motiiviga probleemid.
Võrrandid on invariantsed kalibratsiooniteisenduste ja orientatsiooni hoidvate sümmeetriateisenduste suhtes. Suure korral määrab raadiusega 2-sfääri kujutise vastavale orbiidile ning selle kujutise homotoopset klassi nimetatakse magnetlaenguks. Suurem osa tööd on tehtud juhu G = SU(2) jaoks, kus laenguks on positiivne täisarv k. Funktsionaali globaalne miinimumväärtus on sel juhul 8πk ning asümptootilises arenduses esinev liige m on väärtusega k / 2.
Esimese SU(2) lahenduse tuletasid E. B. Bogomolny, J. K. Parasad ja C. M. Sommerfeld aastal 1975.
1980. aastal näitas C. H. Taubes[48] gluing konstruktsiooni kasutades, et eksisteerivad lahendused kõigi suurte k-de jaoks ning peagi tuletati täpsed telgsümmeetrilised lahendid. Üldjuhu jaoks leidis esimese täpse lahendi 1981. aastal R. S. Ward k = 2 korral.
Bogomolny võrrandite lahendamiseks on 2 võimalust. Esimene neist rakendab twisteri meetodeid. N. J. Hitchini sõnastuses[49] vastab suvaline lahend homomorfsele vektorkimbule üle komplekspinna 1, mis on projektsioonijoone pinnasihiline kimp. Lahend on loomupäraselt isomorfne orienteeritud sirglõikude ruumiga 3-s.
Ääretingimusest ilmneb, et vaadeldav holomorfne kimp on pikenduseks joonkimpudele, mis on määratud (k-1)² sugulusega (genus) algebralise joonega 1-s.
Teise meetodi tuletas W. Nahm[50] ning see kujutab endast seotud Diraci operaatori omaväärtusprobleemi lahendamist ning võrrandite ja vastavate ääretingimuste harilike diferentsiaalvõrrandite süsteemi teisendamist, saades sel viisil Nahmi võrrandid
kus on k × k maatriksfunktsioon kohal (0,2).
Mõlema konstruktsiooni aluseks on analoogsed lahenduskäigud instatonide jaoks, kus konstruktsioonide tuletusviisidele mõeldes tähtsamaid tähelepanekuid oli N. S. Mantoni rakendatud Yang-Millsi võrrandid ruumis 4.
Meetodite ekvivalentsus SU(2) jaoks ning nende põhimõtteline korrektsus määrati töös[51] (vt ka[52]). Täpseid valemeid A ja ϕ jaoks on kummagi meetodi abil keeruline leida, kuigi on olemas mõned täpsed lahendid Nahmi võrrandite jaoks sümmeetrilistel tingimustel.[53]
Üldisema Lie grupi juhtu, kus ϕ stabiliseerimiseks lõpmatuses kasutatakse maksimaalset toroidi, uuris M. K. Murray,[54] lähenedes probleemile twisteri meetodil, kus SU(2) monopooluse üksik spektraalkõver asendatakse joonte kogumiga, mis on nummerdatud vastava Lie grupi Dynkini diagrammi keeriste järgi. Sellele vastava Nahmi esituse tuletasid J. Hustubise ja Murray.[55]
Taubes[56] näitas, et Laenguga k SU(2) monopooluste mooduliruum on sile mittekompaktne 4k – 1 mõõtmeline muutkond. Jättes välja kalibratsiooniteisendused, kus ühendus lõpmatuses ei säili, jääb alles 4k-mõõtmeline muutkond , mis on tõelise mooduliruumi kohal olev ringkimp ning millel on loomupärane täielik hüper-Kähleri meetrika[57] (vt Kähleri-Einsteini muutkond).
Seda meetrikat käsitletakse twisterina[57] ning selle Kähleri potentsiaali saab kirja panna kasutades spektraalkõvera Riemanni teetafunktsioone,[52] kuid vaid k = 2 juht on üldlevinud ja kasutataval kujul teada[57] (alates aastast 2000). See Atiyah–Hitchini muutkond, Einsteini Taub-NUT meetrika ning 4 on ainsad neljamõõtmelised täielikud hüper-Kähler muutkonnad, millel on mittetriholomorfne SU(2) mõjufunktsioon.
Tsükliline k-kordne jaotuste rõngas on isomeetriliselt saadus, kus on tugevalt keskpunkti surutud monopooluste ruum. See ruum esineb ka teoreetilises füüsikas S-duaalsuse ühes rakenduses ning töös[58] uurisid G. B. Segal ja A. Selby selle topoloogiat ja sellel defineeritud L² harmoonilisi vorme, seeläbi osaliselt füüsikalisi ennustusi kinnitades.
Magnetilist monopoolust hüperboolsel kolmruumil uuris twisteri meetodil M. F. Atiyah[59] (asendades komplekspinna TP1 P1×P1 antidiagonaali täiendiga (complement)) ning diskreetsete Nahmi võrrandite meetodil Murray ja M. A. Singer.[60]
Vaata ka
[muuda | muuda lähteteksti]Viited
[muuda | muuda lähteteksti]- ↑ Dark Cosmos: In Search of Our Universe's Missing Mass and Energy, by Dan Hooper, p192
- ↑ Particle Data Group summary of magnetic monopole search
- ↑ Wen, Xiao-Gang; Witten, Edward, Electric and magnetic charges in superstring models, Nuclear Physics B, Volume 261, p. 651–677
- ↑ S. Coleman, The Magnetic Monopole 50 years Later, reprinted in Aspects of Symmetry
- ↑ 5,0 5,1 5,2 C. Castelnovo, R. Moessner and S. L. Sondhi (3. jaan 2008). "Magnetic monopoles in spin ice". Nature. 451: 42–45. arXiv:0710.5515. Bibcode:2008Natur.451...42C. DOI:10.1038/nature06433.
{{cite journal}}: CS1 hooldus: kasutab parameetrit autorid (link) - ↑ 6,0 6,1 6,2 Ray, M.W.; Ruokokoski, E.; Kandel, S.; Möttönen, M.; Hall, D. S. (2014). "Observation of Dirac monopoles in a synthetic magnetic field". Nature. 505 (7485): 657–660. arXiv:1408.3133. Bibcode:2014Natur.505..657R. DOI:10.1038/nature12954. ISSN 0028-0836.
- ↑ The encyclopædia britannica, Volume 17, p352
- ↑ Principles of Physics by William Francis Magie, p424
- ↑ Pierre Curie, Sur la possibilité d'existence de la conductibilité magnétique et du magnétisme libre (On the possible existence of magnetic conductivity and free magnetism), Séances de la Société Française de Physique (Paris), p76 (1894). Free access online copy.
- ↑ Paul Dirac, "Quantised Singularities in the Electromagnetic Field". Proc. Roy. Soc. (London) A 133, 60 (1931). Free web link.
- ↑ 11,0 11,1 Lecture notes by Robert Littlejohn, University of California, Berkeley, 2007–8
- ↑ 12,0 12,1 P. B. Price; E. K. Shirk; W. Z. Osborne; L. S. Pinsky (25. aug 1975). "Evidence for Detection of a Moving Magnetic Monopole". Physical Review Letters. American Physical Society. 35 (8): 487–490. Bibcode:1975PhRvL..35..487P. DOI:10.1103/PhysRevLett.35.487.
- ↑ Blas Cabrera (17. mai 1982). "First Results from a Superconductive Detector for Moving Magnetic Monopoles". Physical Review Letters. American Physical Society. 48 (20): 1378–1381. Bibcode:1982PhRvL..48.1378C. DOI:10.1103/PhysRevLett.48.1378.
- ↑ Milton p.60
- ↑ 15,0 15,1 Polchinski, arXiv 2003
- ↑ 16,0 16,1 "Magnetic Monopoles Detected in a Real Magnet for the First Time". Science Daily. 4. sept 2009. Vaadatud 4. sept 2009.
- ↑ 17,0 17,1 Making magnetic monopoles, and other exotica, in the lab, 29. jaan 2009. Retrieved 31. jaan 2009.
- ↑ 18,0 18,1 Magnetic monopoles spotted in spin ices, September 3, 2009. "Oleg Tchernyshyov at Johns Hopkins University [a researcher in this field] cautions that the theory and experiments are specific to spin ices, and are not likely to shed light on magnetic monopoles as predicted by Dirac."
- ↑ 19,0 19,1 Elizabeth Gibney (29. jaan 2014). "Quantum cloud simulates magnetic monopole". Nature (news section). DOI:10.1038/nature.2014.14612. "This is not the first time that physicists have created monopole analogues. In 2009, physicists observed magnetic monopoles in a crystalline material called spin ice, which, when cooled to near-absolute zero, seems to fill with atom-sized, classical monopoles. These are magnetic in a true sense, but cannot be studied individually. Similar analogues have also been seen in other materials, such as in superfluid helium.... Steven Bramwell, a physicist at University College London who pioneered work on monopoles in spin ices, says that the [2014 experiment led by David Hall] is impressive, but that what it observed is not a Dirac monopole in the way many people might understand it. "There's a mathematical analogy here, a neat and beautiful one. But they're not magnetic monopoles."
- ↑ The fact that the electric and magnetic fields can be written in a symmetric way is specific to the fact that space is three-dimensional. When the equations of electromagnetism are extrapolated to other dimensions, the magnetic field is described as being a rank-two antisymmetric tensor, whereas the electric field remains a true vector. In dimensions other than three, these two mathematical objects do not have the same number of components.
- ↑ "Arhiivikoopia". Originaali arhiivikoopia seisuga 16. oktoober 2014. Vaadatud 8. jaanuaril 2015.
{{netiviide}}: CS1 hooldus: arhiivikoopia kasutusel pealkirjana (link) - ↑ Parker, C.B. (1994). McGraw-Hill Encyclopaedia of Physics (2nd ed.). McGraw-Hill. ISBN 0-07-051400-3.
- ↑ M. Mansfield, C. O'Sullivan (2011). Understanding Physics (4th ed.). John Wiley & Sons. ISBN 978-0-47-0746370.
- ↑ 24,0 24,1 F. Moulin (2001). "Magnetic monopoles and Lorentz force". Nuovo Cimento B. 116 (8): 869–877. arXiv:math-ph/0203043. Bibcode:2001NCimB.116..869M.
- ↑ Wolfgang Rindler (november 1989). "Relativity and electromagnetism: The force on a magnetic monopole". American Journal of Physics. American Journal of Physics. 57 (11): 993–994. Bibcode:1989AmJPh..57..993R. DOI:10.1119/1.15782.
- ↑ For the convention where magnetic charge has units of webers, see Jackson 1999. In particular, for Maxwell's equations, see section 6.11, equation (6.150), page 273, and for the Lorentz force law, see page 290, exercise 6.17(a). For the convention where magnetic charge has units of ampere-meters, see (for example) arXiv:physics/0508099v1, eqn (4).
- ↑ J.A. Heras, G. Baez (2009). "The covariant formulation of Maxwell's equations expressed in a form independent of specific units". arXiv:0901.0194.
{{cite journal}}: viitemall journal nõuab parameetrit|journal=(juhend) - ↑ F. Moulin (2002). "Magnetic monopoles and Lorentz force". arXiv:math-ph/0203043.
{{cite journal}}: viitemall journal nõuab parameetrit|journal=(juhend) - ↑ Shanmugadhasan, S. "The Dynamical Theory of Magnetic Monopoles", Canadian Journal of Physics Vol. 30, p. 218. (1952).
- ↑ 30,0 30,1 Fryberger, D. "On Generalized Electromagnetism and Dirac Algebra", Foundations of Physics Vol. 19, p. 125 (1989).
- ↑ 31,0 31,1 31,2 Jackson 1999, section 6.11.
- ↑ Jackson 1999, section 6.11, equation (6.153), page 275
- ↑ Zel'dovich, Ya.; Khlopov, M. Yu. (1978). "On the concentration of relic monopoles in the universe". Phys. Lett. B79 (3): 239–41. Bibcode:1978PhLB...79..239Z. DOI:10.1016/0370-2693(78)90232-0.
- ↑ Preskill, John (1979). "Cosmological production of superheavy magnetic monopoles". Phys. Rev. Lett. 43 (19): 1365. Bibcode:1979PhRvL..43.1365P. DOI:10.1103/PhysRevLett.43.1365.
- ↑ Preskill, John (1984). "Magnetic Monopoles". Ann. Rev. Nucl. Part. Sci. 34: 461. Bibcode:1984ARNPS..34..461P. DOI:10.1146/annurev.ns.34.120184.002333.
- ↑ Rees, Martin. (1998). Before the Beginning (New York: Basic Books) p. 185 ISBN 0-201-15142-1
- ↑ http://www.nature.com/nature/journal/v429/n6987/full/429010a.html
- ↑ Alvarez, Luis W. "Analysis of a Reported Magnetic Monopole". Kirk, W. T. (toim). Proceedings of the 1975 international symposium on lepton and photon interactions at high energies. International symposium on lepton and photon interactions at high energies, Aug 21, 1975. Lk 967. Originaali arhiivikoopia seisuga 4. veebruar 2009. Vaadatud 9. jaanuaril 2015.
- ↑ "If the structures of the magnetic fields appear to be magnetic monopoles, that are macroscopic in size, then this is a wormhole." Taken from All About Space, issue No. 24, April 2014, item "Could wormholes really exist?"
- ↑ 40,0 40,1 "Quantised Singularities in the Electromagnetic Field" Paul Dirac, Proceedings of the Royal Society, May 29, 1931. Retrieved February 1, 2014.
- ↑ 41,0 41,1 Elizabeth Gibney (29. jaan 2014). "Quantum cloud simulates magnetic monopole". Nature (news section). DOI:10.1038/nature.2014.14612.
- ↑ Zhong, Fang; Naoto Nagosa, Mei S. Takahashi, Atsushi Asamitsu, Roland Mathieu, Takeshi Ogasawara, Hiroyuki Yamada, Masashi Kawasaki, Yoshinori Tokura, Kiyoyuki Terakura (3. okt 2003). "The Anomalous Hall Effect and Magnetic Monopoles in Momentum Space". Science 302 (5642) 92–95. doi:10.1126/science.1089408. ISSN 1095-9203. http://www.sciencemag.org/cgi/content/abstract/302/5642/92. Retrieved 2. aug 2007.
- ↑ Inducing a Magnetic Monopole with Topological Surface States, American Association for the Advancement of Science (AAAS) Science Express magazine, Xiao-Liang Qi, Rundong Li, Jiadong Zang, Shou-Cheng Zhang, January 29, 2009. Retrieved January 31, 2009.
- ↑ Artificial Magnetic Monopoles Discovered
- ↑ 45,0 45,1 S. T. Bramwell, S. R. Giblin, S. Calder, R. Aldus, D. Prabhakaran, T. Fennell (15. okt 2009). "Measurement of the charge and current of magnetic monopoles in spin ice". Nature. 461: 956–959. arXiv:0907.0956. Bibcode:2009Natur.461..956B. DOI:10.1038/nature08500.
{{cite journal}}: CS1 hooldus: kasutab parameetrit autorid (link) - ↑ 46,0 46,1 S. R. Giblin, S. T. Bramwell, P. C. W. Holdsworth, D. Prabhakaran & I. Terry (13. veebr 2011). "Creation and measurement of long-lived magnetic monopole currents in spin ice". 7 (3). Nature Physics. Bibcode:2011NatPh...7..252G. DOI:10.1038/nphys1896. Vaadatud 28. veebr 2011.
{{cite journal}}: viitemall journal nõuab parameetrit|journal=(juhend)CS1 hooldus: mitu nime: autorite loend (link) - ↑ D.J.P. Morris, D.A. Tennant, S.A. Grigera, B. Klemke, C. Castelnovo, R. Moessner, C. Czter-nasty, M. Meissner, K.C. Rule, J.-U. Hoffmann, K. Kiefer, S. Gerischer, D. Slobinsky, and R.S. Perry (3. sept 2009) [2009-07-09]. "Dirac Strings and Magnetic Monopoles in Spin Ice Dy2Ti2O7". Science. 326 (5951): 411–4. Bibcode:2009Sci...326..411M. DOI:10.1126/science.1178868.
{{cite journal}}: CS1 hooldus: mitu nime: autorite loend (link) - ↑ A.Jaffe, C.H.Taubes (1980). Vortices and monopoles.
- ↑ N.J. Hitchin (1982). Monopoles and geodesics.
- ↑ W.Nahm (1982). The construction of all self-dual monopoles by the ADHM method.
- ↑ N.J. Hitchin (1983). On the construction of monopoles.
- ↑ 52,0 52,1 N.J. Hitchin (1999). Integrable sustems in Riemannian geometry (K.Uhlenbeck ed.). C-L.Terng (ed.).
- ↑ N.J. Hitchin, N.S. Manton, M.K. Murray (1995). Symmetric Monopoles.
{{cite book}}: CS1 hooldus: mitu nime: autorite loend (link) - ↑ M.K.Murray (1983). Monopoles and spectral curves for arbitrary Lie groups.
- ↑ J. Hurtubise, M.K. Murray (1989). On the construction of Monopoles for the classical groups.
- ↑ C.H.Taubes (1983). Stability in Yang–Mills theories.
- ↑ 57,0 57,1 57,2 M.F. Atiyah; N.J. Hitchin (1988). The geometry and dynamics of magnetic monopoles. Princeton Univ.Press.
{{cite book}}: CS1 hooldus: mitu nime: autorite loend (link) - ↑ G.B.Segal, A.Selby (1996). The cohomology of the space of magnetic monopoles.
- ↑ M.F.Atiyah (1987). Magnetic monopoles in hyperbolic space, Vector bundles on algebraic varieties. Oxford University Press.
- ↑ M.K.Murray (2000). On the complete integrability of the discrete Nahm equations.
Välislingid
[muuda | muuda lähteteksti]- Magnetic Monopole Searches (lecture notes)
- Particle Data Group summary of magnetic monopole search
- 'Race for the Pole' Dr David Milstead Freeview 'Snapshot' video by the Vega Science Trust and the BBC/OU.
- Interview with Jonathan Morris about magnetic monopoles and magnetic monopole quasiparticles. Drillingsraum, April 16, 2010
- Nature, 2009
- Sciencedaily, 2009
































![{\displaystyle {\frac {dp_{\alpha }}{d\tau }}={\frac {1}{c}}\left[q_{\mathrm {e} }F_{\alpha \beta }v^{\beta }+q_{\mathrm {m} }{\star F_{\alpha \beta }}v^{\beta }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9065594bc7bdcabdfb2330e37e74e4f0f8b45019)








































![{\displaystyle {\frac {dT_{1}}{ds}}=[T_{2},T_{3}],\ \ {\frac {dT_{2}}{ds}}=[T_{3},T_{1}],\ \ {\frac {dT_{3}}{ds}}=[T_{1},T_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6891d198520db75753f0ac078fa1b273801a7776)





