Mine sisu juurde

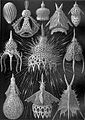
Mustrid looduses

Allikas: Vikipeedia
Tuule moodustatud düünid kõrbeliivas

Mustrid looduses on nähtavad vormilised korrapärad, mida looduses leidub. Neid mustreid esineb erinevates nähtustes ja objektides ning need võivad olla matemaatiliselt modelleeritavad. Looduslike mustrite hulka kuuluvad sümmeetriad, puud, spiraalid, meandrid, lained, vahud, tesselatsioonid, praod ja triibud[1]. Ka varased kreeka filosoofid Platon, Pythagoras ja Empedokles püüdsid seletada korrapärasusi looduses.

19. sajandil uuris Belgia füüsik Joseph Plateau seebikilesid, mille tulemusel sõnastas ta minimaalpinna mõiste. Saksa bioloog ja kunstnik Ernst Haeckel maalis sadu mereorganisme, et näidata nende sümmeetriat. Šoti bioloog D’Arcy Thompson oli loomade ja taimede kasvumustrite uurimise pioneer. Ta tõestas, et spiraalset kasvu saab seletada lihtsate valemitega. 20. sajandil ennustas Briti matemaatik Alan Turing morfogeneesi toimemehhanisme, mis põhjustavad loomadel täpilisi ja triibulisi mustreid. Ungari bioloog Aristid Lindenmayer ja prantsuse-ameerika matemaatik Benoit Mandelbrot näitasid, kuidas fraktalite matemaatika võib tekitada taimede kasvumustreid.

Looduslikke mustreid saab erinevatel tasanditel seletada nii matemaatika, füüsika kui ka keemia abil. Elusolenditel leiduvaid mustreid saab seletada ka loodusliku ja sugulise valikuga.

Ajalugu

[muuda | muuda lähteteksti]

Varased Kreeka filosoofid üritasid seletada korda looduses, nähes ette tänapäevaseid mõisteid. Platon (u 427 – u 347 eKr) arutles oma looduslike mustrite kohta käivates töödes universaalide olemasolu üle. Tema meelest olid looduslikud mustrid ideaalvormide ebatäiuslikud koopiad. Näiteks võib lill olla enam-vähem ringikujuline, kuid pole mitte kunagi täiuslik ring.[2] Pythagoras seletas, et mustrid looduses on nagu muusikalised harmooniad, mis pärinevad numbrist. Number oli tema jaoks eksistentsi põhiline koostisosa.[3] Empedokles jõudis teatud määral järeldusteni, mis sarnanesid Darwini evolutsiooniliste seletustega organismistruktuuride kohta.[4]

1202. aastal tutvustas Leonardo Fibonacci (u 1170 – u 1250) oma raamatus "Liber Abaci"[5] läänemaailmale Fibonacci jada. Fibonacci tõi (ebarealistliku) bioloogilise näite arvulisest kasvust teoreetilises jänesepopulatsioonis.[6] Aastal 1917 avaldas D’Arcy Wentworth Thompson (1860–1948) oma raamatu "On Growth and Form". Tema kirjeldus leheseisu ja Fibonacci jada kohta on klassika. Ta näitas, et lihtsad võrrandid võivad kirjeldada kõiki keerulisena näivaid spiraalse kasvu mustreid loomasarvedel ja molluskite karpidel.[7]

Belgia füüsik Joseph Plateau (1801–1883) uuris põhjalikult seebikilesid ning sõnastas Plateau seaduse, mis kirjeldab seebikiledes tekkivaid struktuure.[8]

Saksa psühholoog Adolf Zeising (1810–1876) väitis, et kuldlõige on näha taimeosades, loomade luustikes ning harulistes veresoonte ja närvide mustrites, aga ka kristallide geomeetrias.[9][10][11]

Ernst Haeckel (1834–1919) maalis illustratsioone mereorganismidest, näidates nende sümmeetriat.[12]

Ameerika fotograaf Wilson Bentley (1865–1931) tegi aastal 1885 esimesena mikroskoobifoto lumehelbest.[13]

Aastal 1951 kirjutas Alan Turing (1912–1954) analüüsi mehhanismidest, mis on vajalikud, et luua mustreid elusorganismides. Seda protsessi nimetatakse morfogeneesiks.[14]

Aastal 1968 töötas Ungari teoreetiline bioloog Aristid Lindenmayer (1925–1989) välja L-süsteemi. See on formaalne grammatika, mida võib kasutada, et modelleerida taimede fraktaalseid kasvumustreid.[15]

Põhjused

[muuda | muuda lähteteksti]

Elusorganismidel nagu näiteks orhideedel, koolibridel ja paabulindudel on välimuses näha ilus vorm, muster ja värvus. Ilu, mida inimesed looduses tajuvad, on tingitud mitmetest teguritest (olenevalt sellest, mida täpselt põhjendada tahetakse).

Matemaatika püüab avastada ja seletada kõiksugu mustreid ja seaduspärasusi.[16][17] Visuaalseid mustreid looduses seletatakse kaoseteooriaga, fraktaalsusega, logaritmiliste spiraalidega, topoloogiaga ja teiste matemaatiliste mudelitega. Näiteks saab L-süsteemide abil moodustada üsna täpseid mudeleid erinevatest puukasvu mustritest.[15]

Füüsikaseadused toovad matemaatilised abstraktsioonid pärismaailma, tihti peaaegu täiuslikult. Näiteks kristall on täiuslik kui sellel ei ole struktuurseid defekte ning kui see on ideaalselt sümmeetriline. Tegelikult ei ole täielik matemaatiline perfektsus reaalsete objektide puhul võimalik.[18] Nähtavad mustrid looduses on loodud füüsikaseaduste poolt, näiteks meandreid saab seletada, kasutades vedelikudünaamikat.

Bioloogias võib looduslik valik põhjustada mustrite teket elusorganismides mitmel põhjusel, sealhulgas varjevärvuseks[19], suguliseks valikuks[19] ja mimikriks.[20] Tihti on lillede kuju, värvus ja mustrid arenenud putuktolmlemise soodustamiseks. Meemesilasi ja teisi tolmeldavaid putukaid meelitavad lillede radiaalsed mustrid, triibud, värvid, lõhnad, kuid ka nektar ja söödav õietolm.[21]

Mustrite tüübid

[muuda | muuda lähteteksti]

Sümmeetriad

[muuda | muuda lähteteksti]

Sümmeetria on elusorganismide seas levinud. Loomadel esineb peamiselt bilateraalne sümmeetria või peegelsümmetria nagu ka taimelehtedel ning mõnedel lilledel, näiteks orhideedel. Tihti on taimedel radiaalne või pöördsümmeetria, viimaseid esineb ka mitmetel loomadel, näiteks meriroosilistel.[22]

Elutute asjade seas on lumehelvestel kuuekandiline sümmeetria. Iga lumehelves on unikaalne ning selle struktuur salvestab endasse infot muutuvatest tingimustest lumehelbe kritalliseerumise ajast. Lumehelbel on kuus haru ning igal harul on samasugune kasvumuster.[23] Kristallidel esineb mitmeid erinevaid sümmeetriaid ning haabitusi, need võivad olla kuubikujulised või oktaeedrilised.[24] Pöördsümmetriat esineb paljudel elututel objektidel, näiteks planeedid on pöördsümmeetrilised.[25]

Sümmeetrial on mitu põhjust. Radiaalne sümmeetria sobib organismidele nagu meriroosid, kelle täiskasvanud isendid ei liigu ning kellele toit ja oht võivad läheneda igast suunast. Kuid loomad, kes liiguvad, omavad vajalikku ülemist ja alumist poolt, pea ja sabaotsa ning vasakut ja paremat külge. Seega on nende kehad bilateraalselt sümmeetrilised (kuigi siseelundid mitte tingimata).[26]

Puud, fraktalid

[muuda | muuda lähteteksti]

Fraktalid on lõputult endasarnased korduvad matemaatilised kujundid, millel on mittetäisarvuline dimensionaalsus.[27][28][29] Lõputu korduvus ei ole looduses võimalik, seega on kõik "fraktaalsed" vormid ainult ligilähedased.

Näiteks sõnajalgtaimede ja sarikaliste lehed on endasarnased ainult 2, 3 või 4 tasandil. Sõnajalgtaimede omadega sarnaseid mustreid võib leida ka teistelt taimedelt, kuid ka loomadelt ning elututelt asjadelt – näiteks võivad elektrilaengud teatud keskkondades levides olla sarnase kujuga.

  • Fraktaalsed spiraalid: Brokoli koosneb endasarnastest vormidest
    Fraktaalsed spiraalid: Brokoli koosneb endasarnastest vormidest
  • Heinputke lillepea on sfäär, mis koosneb sfääridest (endasarnasus)
    Heinputke lillepea on sfäär, mis koosneb sfääridest (endasarnasus)
  • Lichtenbergi kujund
    Lichtenbergi kujund
  • Dendriitilised vasekristallid (mikroskoobis)
    Dendriitilised vasekristallid (mikroskoobis)

Spiraalid

[muuda | muuda lähteteksti]

Spiraalid on tavapärased taimedel ja mõnedel loomadel, enim molluskitel. Näiteks nautilusel on iga koja kamber järgneva ligilähedane koopia, mille suurus on määratud konstantse teguriga ning seatud logaritmilisse spiraali.[30]

Taimespiraale võib näha taimede leheseisudel ning lillepeadel ja seemnepeadel, näiteks päevalilledel. Neid struktuure saab seletada mitmel tasandil – matemaatikaga, füüsikaga, keemiaga ja bioloogiaga.

Füüsikalisest vaatenurgast on spiraalid kõige vähem energiat nõudvad moodustised[31], mis tekivad dünaamistes süsteemides iseeneslikult iseorganiseeruva protsessi tulemusel.[32] Leheseisu kontrollivad proteiinid, mis manipuleerivad taime hormooni auksiini kontsentratsiooniga. Bioloogilisest vaatenurgast on lehtede asetamine üksteisest võimalikult kaugele kasulik loodusliku valiku seisukohast, kuna see suurendab ligipääsu ressurssidele, eriti päikesevalgusele.[33]

Meandrid

[muuda | muuda lähteteksti]

Meandrid on looked jõgedes ja teistes kanalites. Meandrid moodustuvad, sest jõe vool on alati turbulentne ning reljeef pole kunagi absoluutselt ühtlase kallakuga. Seetõttu ei saa kujuneda sirgeid jõesänge. Tekkinud looked muutuvad suuremaks, sest jõed voolavad väliskurvis kiiremini ja erodeerivad sealt setteid, mille tulemusel tekib kõrge kaldaga põrkeveer. Sisekurvis toimub aga aeglase voolu tõttu setete kuhjumine (jõgi säilitab oma laiuse, kuid muudab asukohta). Seega on tegemist positiivse tagasisidega – tekkinud jõelooge soodustab enda edasist arenemist.[34]

Lained, düünid

[muuda | muuda lähteteksti]

Laineks nimetatakse võnkumise levimisprotsessi ruumis. Mehaanilised lained levivad mingis keskkonnas, näiteks õhus või vees. Lained panevad läbitava keskkonna võnkuma.

Vee või tuule lained liigutavad liiva ning tekitavad lainetavaid mustreid. Kui tuul puhub üle suurte liivaväljade, siis tekivad düünid. Düünidest võib moodustuda mitmesuguseid mustreid. Need mustrid võivad olla näiteks sirbi-, tähe- või paraboolikujulised, kuid ka lihtsalt pikad sirged jooned.[35]

Mullid, vahud

[muuda | muuda lähteteksti]

Mull moodustab sfääri, mis on väikseima võimaliku pindalaga kujund etteantud ruumala puhul. Vaht on mullide kogum. Looduses leidub erinevast materjalist vahte.

Rakutasandil on vahumustrid tavapärased. Aulonia hexagona skelett näeb välja, nagu see koosneks täielikult kuusnurkadest, kuigi see on matemaatiliselt võimatu.[36]

Tesselatsioonid

[muuda | muuda lähteteksti]

Tesselatsioonid on mustrid, mille moodustavad korduvad plaadid lamedal pinnal. Herilaspesad ja meekärjed on head näited looduslikest tesselatsioonidest. Tesselatsioone võib leida ka taimedelt, näiteks on kirju püvilille kroonlehtedel malelauda meenutav muster. Samuti võib tesselatsioone leida mitmete roomajate nahalt.[37]

Praod

[muuda | muuda lähteteksti]

Praod on lineaarsed avaused, mis tekivad materjalidesse pingete vabanemise tulemusel.

  • Kuivav muda peamiselt 90 kraadiste pragudega
    Kuivav muda peamiselt 90 kraadiste pragudega
  • Tardunud basalt Giant Causeways Iirimaal. Näha on püstised praod, mis on ümbritsevate pragudega peamiselt 120-kraadise nurga all. Seetõttu on tekkinud kuusnurksed sambad.
    Tardunud basalt Giant Causeways Iirimaal. Näha on püstised praod, mis on ümbritsevate pragudega peamiselt 120-kraadise nurga all. Seetõttu on tekkinud kuusnurksed sambad.

Täpid, triibud

[muuda | muuda lähteteksti]

Leopardid ja lepatriinud on täpilised ning sebrad triibulised.[38] Neil mustritel on evolutsiooniline seletus: need suurendavad tõenäousust, et looma järglane jääb paljunemiseks ellu. Üks loomamustrite funktsioone on varjevärvus.[19] Näiteks leopardi täpid muudavad saakloomadele tema märkamise raskemaks. Teine funktsioon on hoiatusvärvus,[20] näiteks on lepatriinul väiksem oht sattuda linnurünnaku ohvriks, kui tal on hoiatusvärvid.

Viited

[muuda | muuda lähteteksti]
  1. ↑ Stevens, Peter. Patterns in Nature, 1974. lehekülg 3.
  2. ↑ Balaguer, Mark (07.04.2009) [2004]. "Stanford Encyclopedia of Philosophy". Platonism in Metaphysics. Stanfordi Ülikool. vaadatud 04.05.2012.
  3. ↑ The so-called Pythagoreans, who were the first to take up mathematics, not only advanced this subject, but saturated with it, they fancied that the principles of mathematics were the principles of all things. Aristoteles, Metaphysics 1–5 , cc. 350 BC
  4. ↑ Aristotle reports Empedocles arguing that, "[w]herever, then, everything turned out as it would have if it were happening for a purpose, there the creatures survived, being accidentally compounded in a suitable way; but where this did not happen, the creatures perished." The Physics, B8, 198b29 in Kirk, et al., 304).
  5. ↑ Singh, Parmanand. Acharya Hemachandra and the (so called) Fibonacci Numbers. Math. Ed. Siwan, 20(1):28–30, 1986. ISSN 0047-6269
  6. ↑ Knott, Ron. "Fibonacci's Rabbits". University of Surrey Faculty of Engineering and Physical Sciences.
  7. ↑ About D'Arcy. D' Arcy 150. University of Dundee and the University of St Andrews. vaadatud 16.10.2012.
  8. ↑ Stewart, Ian. 2001. leheküljed 108–109.
  9. ↑ Padovan, Richard (1999). Proportion. Taylor & Francis. pp. 305–306. ISBN 978-0-419-22780-9.
  10. ↑ Padovan, Richard (2002). "Proportion: Science, Philosophy, Architecture". Nexus Network Journal 4 (1): 113–122.doi:10.1007/s00004-001-0008-7.
  11. ↑ Zeising, Adolf (1854). Neue Lehre van den Proportionen des meschlischen Körpers. eessõna.
  12. ↑ Ball, Philip. Shapes. 2009. lehekülg 41.
  13. ↑ Hannavy, John (2007). Encyclopedia of Nineteenth-Century Photography 1. CRC Press. p. 149. ISBN 0-415-97235-3.
  14. ↑ Turing, A. M. (1952). "The Chemical Basis of Morphogenesis". Philosophical Transactions of the Royal Society B237 (641): 37–72. Bibcode:1952RSPTB.237...37T. doi:10.1098/rstb.1952.0012.
  15. ↑ 15,0 15,1 Rozenberg, Grzegorz; Salomaa, Arto. The mathematical theory of L systems. Academic Press, New York, 1980.ISBN 0-12-597140-0
  16. ↑ Steen, L.A.. The Science of Patterns. Science, 240: 611–616, 1998. Kokkuvõte aadressil ascd.org
  17. ↑ Devlin, Keith. Mathematics: The Science of Patterns: The Search for Order in Life, Mind and the Universe (Scientific American Paperback Library) 1996
  18. ↑ Tatarkiewicz, Władysław. Perfection in the Sciences. II. Perfection in Physics and Chemistry, Dialectics and Humanism, vol. VII, no. 2 (spring 1980), lk 139.
  19. ↑ 19,0 19,1 19,2 Darwin, Charles. On the Origin of Species. 1859, peatükk 4.
  20. ↑ 20,0 20,1 Wickler, W. (1968). Mimicry in plants and animals. New York: McGraw-Hill.
  21. ↑ Koning, Ross (1994). "Plant Physiology Information Website". Pollination Adaptations. Ross Koning. vaadatud 02.05.2012.
  22. ↑ Stewart, Ian. 2001. leheküljed 64–65.
  23. ↑ Stewart, Ian. 2001. lehekülg 52.
  24. ↑ Stewart, Ian. 2001. leheküljed 82–84.
  25. ↑ Stewart, Ian. 2001. lehekülg 71.
  26. ↑ Hickman, Cleveland P.; Roberts, Larry S.; Larson, Allan (2002). "Animal Diversity" (PDF). Chapter 8: Acoelomate Bilateral Animals (Third ed.). McGraw-Hill. lk 139. vaadatud 25.10.2012.
  27. ↑ Mandelbrot, Benoît B. (1983). The fractal geometry of nature. Macmillan.
  28. ↑ Falconer, Kenneth (2003). Fractal Geometry: Mathematical Foundations and Applications. John Wiley.
  29. ↑ Briggs, John (1992). Fractals:The Patterns of Chaos. Thames and Hudson. lk 148.
  30. ↑ Maor, Eli. e: The Story of a Number. Princeton University Press, 2009. lk 135.
  31. ↑ (subscription required)
  32. ↑ Douady, S; Couder, Y. (March 1992). "Phyllotaxis as a physical self-organized growth process". Physical Review Letters 68 (13): 2098–2101. Bibcode:1992PhRvL..68.2098D. doi:10.1103/PhysRevLett.68.2098. PMID 10045303.
  33. ↑ Kappraff, Jay (2004). "Growth in Plants: A Study in Number" (PDF). Forma 19: 335–354.
  34. ↑ Lewalle, Jacques (2006). "Flow Separation and Secondary Flow: Section 9.1". Lecture Notes in Incompressible Fluid Dynamics: Phenomenology, Concepts and Analytical Tools. Syracuse, NY: Syracuse University..
  35. ↑ "Types of Dunes". USGS. 29.10.1997. vaadatud 02.05.2012.
  36. ↑ Ball, Philip. Shapes. 2009, lk 51–54.
  37. ↑ Hook, J.R.; Hall, H.E. Solid State Physics (2nd Edition). Manchester Physics Series, John Wiley & Sons, 2010. ISBN 978-0-471-92804-1
  38. ↑ Ball, Philip. Shapes. 2009, lk 156–158.
Pärit leheküljelt "https://et.wikipedia.org/w/index.php?title=Mustrid_looduses&oldid=6576851"