Güroskoop
See artikkel ootab keeletoimetamist. |

Güroskoop (Kreeka keeles: gyros- ring/pöörlemine + skopeo- vaatan/näha) on mehaaniline seade, mille abil saab impulsimomenti arvestades määrata või säilitada liikumise suunda, keerukama seadmega ka ruumilist asendit [1].
Kiires pöörlemises oleval massil, kettal või muul jäigal kehal (rootoril), mille pöördtelg langeb kokku selle sümmeetriateljega, on impulsimoment, mis mõjub välistele jõududele vastupidises suunas, hoides süsteemi muutumatuna. Kui see seade paigaldada ruumitelgede mitmeastmelise pöörlemisvabadusega kardaanliigendile, võib süsteemi keerates täheldada ringliikumises oleva ketta püsimajäämist esialgsele tasandile.
Peale mehaaniliste güroskoopide vurrmehhanismide (elektrilised, pneumaatilised) on muudelgi põhimõtetel töötavaid güroskoope ehk akselomeetreid: kiirendusanduritega mikrokiibid, kiudoptilised ja ülitundlikud kvantgüroskoopid. Güroskoope kasutatakse navigeerimisseadmetes, seda tingimustes, kus traditsioonilise magnetkompassi kasutamine või asendi määramine horisondi suhtes on raskendatud või võimatu, näiteks pilves või kosmoses. Güroskoope kasutatakse laialdaselt lennunduses pimelennul, raadio teel juhitavate mehitamata helikopterite ja lennukite asendit hoidvate autopilootide stabiliseerimisandurina. Veel kasutatakse güroskoopi näiteks tunneli kaevamisel suunahoidjana.[2]
Kõige lihtsamad güroskoobi näited on vurr ja kiirelt pöörlev jalgratta ratas. Seisev vurr ei püsi püsti, aga kui vurr pöörlema panna, hoiab seade end püsti ja kukub alles siis, kui hõõrdest tingitud pöörlemise kiiruse kadu lõpetab güroskoopefektist tulenevad seadet püsti hoidvad jõud.
Omadused[muuda | muuda lähteteksti]
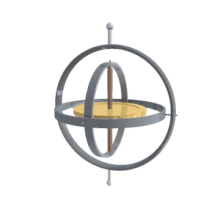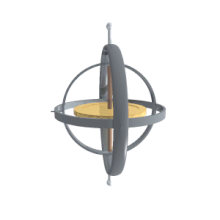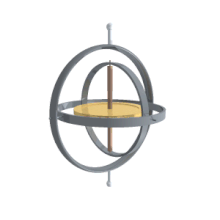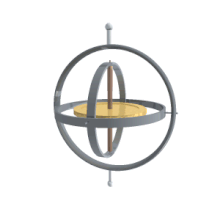
Güroskoobil on mitu toimeviisi, sealhulgas pretsessioon ja nutatsioon. Gürokompassid täiendavad edukalt magnetkompasse laevades, lennukites, kosmosejaamades ja sõidukites, kus magnetkompass on kõikumise ajal häiritud. Güroskoop tagab stabiilse asendi ruumis, näiteks Hubble'i teleskoop. Samuti on güroskoobid asendamatud telemeetrilistes juhtimissüsteemides.
Võrrand, mis kirjeldab güroskoobi toimimist, on järgmine:
kus τ ja L kirjeldavad güroskoobi jõu- ja impulsimomenti, I inertsimomenti, vektor ω nurkkiirust ja α nurkkiirendust.
Eelmisest võrrandist järeldub, et jõumoment τ on pöörlemisteljega risti, seega risti ka impulsimomendiga. Pretsessiooni nurkkiirust kirjeldab valem:

Pretsessiooni selgitamiseks kujutlegem, et kiirelt pöörlev suure erikaaluga ketas (rootor) on asetatud oma tasakaalukeskmele nõnda, et tema telg on kaldu. Võiks arvata, et güroskoop kukub gravitatsioonijõu tõttu ümber, kuid selle asemel jääb ta hoopis maapinnaga risti asetseva kujutletava telje ümber tiirlema. Seejuures joonistab ühest otsast maapinnaga ühenduses oleva güroskoobi tiirlev risttelg tasapinnalise ringi ning kogu süsteem joonistab välja koonuse. Jõumomenti toetavad antud hetkel mitu jõudu, nagu gravitatsioonijõud suunaga Maa keskme suunas ning võrdväärne güroskoopefekti jõud vastassuunaga üles, toetamaks süsteemi stabiilsust. Pöörlemisest tingitud jõumoment ei ole käesoleval hetkel suunatud alla, nagu võiks intuitiivselt oodata, põhjustades seadeldise kukkumist, vaid on risti nii gravitatsioonilise pöördemomendiga (mis on horisontaalne ja risti pöörlemisteljega) ja ühtlasi ka pöörlemise teljega.
Güroskoobi pretsessiooni kiirus ΩP on pöördvõrdeline tema impulsimomendiga L:
kus θ on nurk vektorite ΩP ja L vahel. Seega, kui rootori pöörlemise kiirus väheneb (näiteks hõõrde pärast keha pinnasele toetumise tagajärjel või rootori pinna õhutakistuse tõttu), siis sellest tingituna väheneb impulsimoment ja pretsessioonimäär suureneb. See protsess jätkub, kuni seadeldis ei jõua enam piisava kiirusega pöörelda, et impulsimoment toetaks seadeldise raskust. Kui pretsesseerimise lõppedes ketas kukub, on see tingitud impulsimomendi jõu vähenemisest, mis hoidis seadeldist püsti. Enne pöörlemise lõppemist võib täheldada vurri loperdamist tasakaalulise pretsessiooni ja impulsimomendi vahel, ent hõõrde- ja gravitatsioonjõu mõjul kukub lõplikult peatunud rootor ümber.
Kokkuleppeliselt need vektorid – pöördemoment, pretsessioon ja spinn ehk pöörlemine – on teineteisega orienteeritud parema käe reegli järgi. Lihtsustatult võib öelda, et güroskoopefekt paneb ratta suunda muutma kallakuga samas suunas.
Ajalugu[muuda | muuda lähteteksti]
Vanima teadaoleva güroskoobilaadse instrumendi ehitas sakslane Johann Bohnenberger, kes mainis seda aastal 1817, kutsudes seda masinaks.[3][4] Seadeldis põhines massiivsel keerleval sfääril. Aastal 1832 töötas ameeriklane Walter R. Johnson välja sarnase seadeldise, mis põhines keerleval kettal.[5][6] Matemaatikute soovitusel õppeseadeldiseks kasutusele võetud mehhanism paelus Léon Foucault'd. 1852. aastal kasutas Foucault seadeldist Maa pöörlemise uurimise eksperimentides.[7][8] Just tema andis seadeldisele selle tänapäevase nimetuse tähendusega "näha Maa pöörlemist" (kreeka keeles skopeō – 'vaatan, vaatlen', gyros – 'ring' või 'pöörlemine').[9] Maa pöörlemist ümber oma telje oli märgata 8–10 minuti möödudes. Selle aja sees oli güroskoobi pöörlev ketas nähtavalt oma pöörlemistelge muutnud, ent tegelikult oli Maa end güroskoobi all pööranud, põhjustades näiliselt ketta telje muutuse.
1860. aastatel elektrimootorite kasutuselevõtuga sai güroskoopi panna pöörlema automaatselt ning nii kauaks kui tarvis. Valmis esimene gürokompassi prototüüp. Esimese funktsionaalse gürokompassi patenteeris 1904. aastal saksa leiutaja Hermann Anschutz-Kaempfe. Ameeriklane Elmer Sperry tuli välja omapoolse güroskoobi variandiga sama aasta lõpus ning peagi avastati ka teistes riikides leiutise militaarne kasulikkus.
20. sajandi algus oli aeg, mil merevägi oli üks tähtsamaid riigi sõjalise võimekuse indikaatoreid. Ameeriklaste Sperry Gyroscope Company kasvas kiirelt ning valmistas lennukitele ja laevadele stabiliseerimisseadmeid.
1917. aastal ehitas Chandler Company of Indianapolis "Chandleri güroskoobi", mis oli vurrist mänguasi, mille pöörlema panemiseks pidi tõmbama nööri.
Teises maailmasõjas said güroskoopidest põhilised lennuki- ja õhutõrjerelvade sihikute komponendid.
Tänapäeval kasutatakse MEMS-tehnoloogial güroskoope näiteks kaasaskantavates elektroonikaseadmetes nagu Apple’i viimase põlvkonna iPadis, iPhone’ides ja teistes nutitelefonides. Kiirendusandurid määravad kiirenduse suurust ruumi kolmel teljel ning vastava tarkvara abil kuvatakse kaldenurk nutiseadme ekraanile.
Londoni moment[muuda | muuda lähteteksti]
Londoni momendi güroskoobi toimimispõhimõte toetub kvantmehaanika ilmingule, milles keerlev ülijuht tekitab magnetvälja, mille teljed ühilduvad täpselt pöörleva güroskoobi tekitatud vektoritega. Magnetomeeter määrab genereeritud magnetvälja orientatsiooni, mis on kalibreeritud määramaks güroskoobi pöörlemise telje. Kvantmehaanilisele nähtuse tööpõhimõttele tuginev güroskoop võib olla väga täpne ja stabiilne. Näiteks güroskoope, mida kasutatakse Gravity Probe B eksperimentides, mõõdavad muutusi güroskoobi pöörlemistelje orientatsioonis paremini kui 0,5 milliarcsekundit (1,4×10−7 kraadi) üle ühe aasta jooksul. Selline pöörlemistelje muutuse uurimine on täpsuselt samaväärne juuksekarva läbimõõdu vaatlemisega 32 kilomeetri kauguselt.
Nüüdisaegsed kasutusviisid[muuda | muuda lähteteksti]

Güroskoope kasutatakse kompassides, avioonikas (pöörangunäidik, aviohorisont, gürokompass), arvutihiirtes, laevades ning ka olmeelektroonikas. Kuna güroskoop võimaldab määrata ruumilist asendit horisondi suhtes, seda optiliselt või visuaalselt nägemata, on konstruktorid lisanud neid modernsetesse seadmetesse ja liikurvahendeisse. Tehnoloogia uuenemisel on seadeldise töötäpsus 3D-ruumis paranenud, olles efektiivsem endistest kiirendusanduritest nutitelefonides. Tuntud kriitik Scott Steinberg on öelnud, et uute kiudoptiliste güroskoopide lisamine iPhone 4 toodangusse defineerib uue suhtumise allalaaditavasse tarkvarasse.
Güroskoope kasutatakse ka õppevahenditena kesk- ja ülikoolide füüsikatundides. Demonstratsioonigüroskoobid on tavaliselt ehitatud nii, et seadeldise töötamisel ilmnevad füüsikalised jõud tuleksid selgesti esile. Näiteks võidakse ühele vurri küljele asetada lisaraskusi, et seejärel jälgida güroskoobi reaktsiooni. Samuti on võimalik vurri käes hoides tunda selle güroskoopilist jõudu.
Võimalik on tellida güroskoope sisaldavaid arvutihiiri, mis teevad selle kasutamise võimalikuks ka aluspinnalt õhku tõstetuna. Säärased arvutihiired on juhtmevabad, seega sobivad esitlusteks, kus kõneleja liigub ruumis ringi. Arvutihiires olev güroskoop jälgib käe liikumist tasandi suhtes ja tõlgib need ümber kursori liikumiseks.
Güroskoopilist ilmingut kasutatakse näiteks autospordis. Seda seetõttu, et mootorid toimivad just nagu suured güroskoobid. Olenevalt sellest, kas mootori hooratas (pöörlev mass) pöörleb päri- või vastupäeva, on autole mõjuv güroskoopjõud suunatud kas alla või üles. Kasutades mootori pöördeid ära õige nurga all, on võimalik parandada sõiduki rajal püsimist.
Güroskoopsensoreid kasutatakse virtuaalreaalsuse peakomplektides, mõõtmaks inimese pea liigutusi ja liigutuse kiirusi, millest saadud andmed tõlgendatakse ümber virtuaalreaalsusse.
Peale teaduslike kasutusvaldkondade on güroskoope kasutatud ka mänguasjades. Tuntuimaks on ehk Powerball, mille otstarve on olla esmalt meelelahutuslik, kuid teisalt on see ka lihastele ja liigestele kasulik.
Vaata ka[muuda | muuda lähteteksti]
Viited[muuda | muuda lähteteksti]
- ↑ "Gyroscope" by Sándor Kabai, Wolfram Demonstrations Project.
- ↑ Discover magazine 20 things you didn't know about tunnels (Number 8).
- ↑ Johann G. F. Bohnenberger (1817) "Beschreibung einer Maschine zur Erläuterung der Gesetze der Umdrehung der Erde um ihre Axe, und der Veränderung der Lage der letzteren" (Description of a machine for the explanation of the laws of rotation of the Earth around its axis, and of the change of the orientation of the latter), Tübinger Blätter für Naturwissenschaften und Arzneikunde, vol. 3, pages 72–83.
- ↑ The French mathematician Poisson mentions Bohnenberger's machine as early as 1813: Simeon-Denis Poisson (1813) "Mémoire sur un cas particulier du mouvement de rotation des corps pesans" [Memoir on a special case of rotational movement of massive bodies], Journal de l'École Polytechnique, vol. 9, pages 247–262. Available on-line at: http://www.ion.org/museum/files/File_2.pdf .
- ↑ Walter R. Johnson (January 1832). "Description of an apparatus called the rotascope for exhibiting several phenomena and illustrating certain laws of rotary motion", The American Journal of Science and Art, 1st series, vol. 21, no. 2, pages 265–280.
- ↑ Drawings of Walter R. Johnson's gyroscope ("rotascope") were used to illustrate phenomena in the following lecture: E.S. Snell (1856) "On planetary disturbances," Board of Regents, Tenth Annual Report of the Board of Regents of the Smithsonian Institution.... (Washington, D.C.: Cornelius Wendell, 1856), pages 175–190.
- ↑ L. Foucault (1852) "Sur les phénomènes d’orientation des corps tournants entraînés par un axe fixe à la surface de la terre — Nouveaux signes sensibles du mouvement diurne" (On the phenomena of the orientation of rotating bodies carried along by an axis fixed to the surface of the earth — New perceptible signs of the daily movement), Comptes rendus hebdomadaires des séances de l’Académie des Sciences (Paris), vol. 35, pages 424–427. Available on-line (in French): http://gallica.bnf.fr/ark:/12148/bpt6k2992n/f428.image .
- ↑ Circa 1852, Friedrich Fessel, a German mechanic and former secondary school teacher, independently developed a gyroscope. See: (1) Julius Plücker (September 1853) "Über die Fessel'sche rotationsmachine", Annalen der Physik, vol. 166, no. 9, pages 174–177; (2) Julius Plücker (October 1853) "Noch ein wort über die Fessel'sche rotationsmachine", Annalen der Physik, vol. 166, no. 10, pages 348–351; (3) Charles Wheatstone (1864) "On Fessel's gyroscope", Proceedings of the Royal Society of London, vol. 7, pages 43–48.
- ↑ L. Foucault (1852) Comptes rendus..., vol. 35, page 427.
- ↑ ÕS: vurrkompass
- ↑ EKSS: vurrkompass
Välislingid[muuda | muuda lähteteksti]
| Vikiõpikutes on lisamaterjali: High School Physics/Rotational Motion |
- The Royal Institution’s 1974–75 Christmas Lecture Professor Eric Laithwaite
- One-Wheeled Robot-Gyrostat by Olga Kapustina and Yuri Martynenko Wolfram Demonstrations Project
- The Little Top That Aims a Gun by Gold Sanders, Popular Science July 1945
- Apostolyuk V. Theory and Design of Micromechanical Vibratory Gyroscopes



