Diferentsiaalarvutus
Diferentsiaalarvutus on üks matemaatilise analüüsi põhikomponente integraalarvutuse kõrval (et nad on omavahel tihedalt seotud, siis nimetatakse neid koos diferentsiaal- ja integraalarvutuseks). Diferentsiaalarvutuse keskne teema on funktsiooni lokaalne muutumine.

Selleks kasutatakse funktsiooni tuletise mõistet, mis on diferentsiaalarvutuse põhimõiste. Selle geomeetriline vaste on funktsiooni graafiku puutuja tõus. Tuletis on (Leibnizi ettekujutuse järgi) võrdelisustegur argumendi väärtuse lõpmata väikeste muutude ja funktsiooni väärtuse lõpmata väikeste muutude vahel. Kui niisugune võrdelisustegur (mingil kohal) eksisteerib, siis nimetatakse funktsiooni (sellel kohal) diferentseeruvaks funktsiooniks. Samaväärselt võib tuletist mingil kohal defineerida selle lineaarfunktsioonina, mis lähendab funktsiooni lokaalselt teistest lineaarfunktsioonidest paremini. Sellepärast nimetatakse tuletist ka funktsiooni linearisatsiooniks.
Paljudel juhtudel on diferentsiaalarvutuse kasutamine tegelikkust võimalikult täpselt kujutavate matemaatiliste mudelite konstrueerimisel ja järgneval analüüsimisel möödapääsmatu. Sageli vastab tuletisele tegelikkuses muutumise hetkkiirus, majandusteaduses ka näiteks piirkulud ja piirtootlikkus.
Geomeetria seisukohast on tuletis tõusu üldistus. Tõus on algselt defineeritud ainult lineaarfunktsioonide jaoks (nende graafik on sirge). Suvalise funktsiooni tuletist kohal defineeritakse funktsiooni graafiku puutuja tõusuna punktis .
Aritmeetika seisukohast ütleb funktsiooni tuletis iga koha kohta, kui suur on funktsiooni muudu lineaarosa (1. järku muut), kui argumendi väärtuse muut on kui tahes väike. Selle asjaolu täpseks formuleerimiseks kasutatakse piirväärtuse mõistet.
Klassikalises füüsikalises rakenduses näitab ajast sõltuva koha- või teepikkusefunktsiooni tuletis osakese hetkkiirust. Hetkkiiruse tuletis aja järgi näitab hetkkiirendust.
Tuletise ja diferentseeruvuse definitsioon[muuda | muuda lähteteksti]
 Pikemalt artiklis Tuletis (matemaatika)
Pikemalt artiklis Tuletis (matemaatika) Pikemalt artiklis Diferentseeruv funktsioon
Pikemalt artiklis Diferentseeruv funktsioon
Sissejuhatus[muuda | muuda lähteteksti]
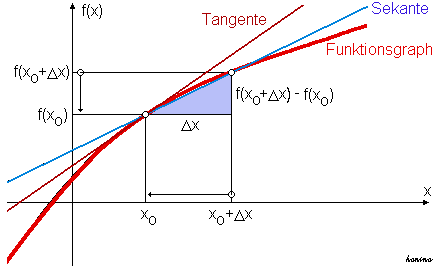
Tuletise definitsiooni lähtekoht on puutuja tõusu lähendamine lõikaja tõusu ehk kõõlu tõusu abil. Otsitagu funktsiooni graafiku tõusu punktis . Kõigepealt arvutatakse funktsiooni lõikaja tõus lõplikus vahemikus:
- Lõikaja tõus = .
Lõikaja tõus on niisiis kahe muudu suhe; sellepärast nimetatakse seda ka muutude suhteks. Tähistades lühidalt kui , saab lõikaja tõusu üles kirjutada kui .
Muutude suhted on igapäevaelust hästi tuntud, näiteks keskmise kiirusena:
- "Sõites Augsburgist Flensburgi olin ma kell 9.43 () Biebelriedi ristil (ööpäeva kilomeetrinäit = 198 km). Kell 11.04 () olin ma Hattenbachi kolmnurgas (ööpäeva kilomeetrinäit =341 km). Seega läbisin ma 1 tunni 21 minutiga () 143 km (). Minu keskmine kiirus sellel lõigul oli seega 143 km / 1,35 h = 106 km/h ()."
Et arvutada puutuja tõusu (siinses rakenduses hetkkiirust), tuleb kahte punkti, millest lõikaja on läbi tõmmatud, teineteisele aina lähemale tuua. Seejuures lähenevad nii kui ka nullile. Suhe jääb aga paljudel juhtudel lõplikuks. Sellel piirprotsessil põhineb järgmine definitsioon:
Diferentseeruvus ja tuletis punktis: formaalne definitsioon ja tähistus[muuda | muuda lähteteksti]
Funktsiooni , mis kujutab vahemiku U reaalarvude hulka, nimetatakse diferentseeruvaks kohal , kui eksisteerib piirväärtus
- ().
Seda piirväärtust nimetatakse funktsiooni tuletiseks järgi kohal ja seda tähistatakse
- või või või .
Avaldisi ja nimetatakse diferentsiaalideks, aga tänapäeva matemaatilises analüüsis (esituse selles kohas) on need ainult sümbolid ning seni tohib neid kasutada ainult sellises tuletise tähistuses. Mõnedes rakendustes (liitfunktsiooni diferentseerimine, mõne diferentsiaalvõrrandi integreerimine asendusreegel integreerimisel) arvutatakse nendega peaaegu nagu tavaliste muutujatega. Sellele annab täpse formaalse põhjenduse diferentsiaalvormide teooria. Diferentsiaal on ka integraalide tavalise tähistuse osa.
Tuletise tähistuse kahe diferentsiaali suhtena võttis kasutusele Leibniz. Newton kasutas punkti selle muutuja peal, mis märgib selle funktsiooni väärtust, millest tuletis võetakse; füüsikas kasutatakse seda tähistust tänini, kui tegu on tuletisega aja järgi (. Kriipsuga tähistus () pärineb Joseph-Louis Lagrange'ilt, kes võttis selle 1797 kasutusele oma raamatus "Théorie des fonctions analytiques".
Aja jooksul leiti järgmine samaväärne definitsioon, mis on osutunud üldisemas kompleksmuutuja või mitmemõõtmeliste funktsioonide puhul mugavamaks:
Funktsiooni nimetatakse punktis diferentseeruvaks, kui eksisteerib niisugune konstant , et
Funktsiooni muutu, kui punktist kaugenetakse ainult pisut, näiteks väärtuse võrra, saab niisiis väga hästi lähendada funktsiooniga, sellepärast nimetatakse lineaarfunktsiooni , kus , ka funktsioni linearisatsiooniks kohal .
Veel üks definitsioon on järgmine: eksisteerivad kohal pidev funktsioon , kusjuures , ja konstant , nii et iga korral
- .
Tingimused, et ja on kohal pidev, tähendavad parajasti seda, et kui läheneb punktile , siis "jääkliige" läheneb nullile.
Mõlemal juhul on konstant üheselt määratud ja .
Selle formuleeringu eeliseks on, et tõestused on lihtsamad, sest ei ole tarvis kasutada jagatist. Seda esitust parima lineaarlähenduse kaudu kasutasid järjekindlalt juba Weierstraß, Henri Cartan ja Jean Dieudonné.
Kui funktsiooni nimetatakse diferentseeruvaks, mainimata kindlat kohta, siis see tähendab, et funktsioon on diferentseeruv igal oma määramispiirkonna kohal ehk funktsiooni graafiku igal punktil on üheselt määratud puutuja.
Tuletis kui funktsioon[muuda | muuda lähteteksti]
 Pikemalt artiklis Tuletisfunktsioon
Pikemalt artiklis Tuletisfunktsioon
Funktsiooni tuletist kohal , mida tähistatakse kirjeldab lokaalselt funktsiooni käitumist vaadeldava koha ümbruses. Aga ei ole ainus koht, millel on diferentseeruv. Sellepärast võib proovida seada igale arvule funktsiooni määramispiirkonnast vastavusse tuletise sellel kohal (). Niiviisi saadakse uus funktsioon mille määramispiirkond on kõigi niisuguste punktide hulk , millel funktsioon on diferentseeruv. Seda funktsiooni nimetatakse funktsiooni tuletisfunktsiooniks ehk lühidalt tuletiseks ja öeldakse, et funktsioon on piirkonnas diferentseeruv. Näiteks on ruutfunktsioonil mis tahes kohal tuletis seega on ruutfunktsioon reaalarvude hulgal diferentseeruv. Vastav tuletisfunktsioon on antud kui
Tuletisfunktsioon erineb tavaliselt algsest funktsioonist, erandiks on eksponentsiaalfunktsiooni kordsed .
Kui funktsiooni tuletis on pidev, siis nimetatakse teda pidevalt diferentseeruvaks funktsiooniks. Määramispiirkonnaga pidevate funktsioonide ruumi tähistatakse , sama määramispiirkonnaga pidevalt diferentseeruvate funktsioonide ruumi tähistatakse .
Tuletiste arvutamine[muuda | muuda lähteteksti]
Funktsiooni tuletise arvutamist nimetatakse funktsiooni diferentseerimiseks
Elementaarfunktsioonide (näiteks , ) arvutamiseks juhindutakse ülal esitatud definitsioonist, arvutatakse muutud suhe ning leitakse piirväärtus, kus läheneb nullile. Koolimatemaatikas nimetatakse seda h-meetodiks. Tüüpiline matemaatika rakendaja teeb selle arvutuse läbi ainult mõned korrad elus. Hiljem ta teab tähtsamate elementaarfunktsioonide tuletisi peast ning harvem esinevate funktsioonide tuletisi vaatab tabelitest (näiteks Bronštein-Semendjajevist või meie tuletiste ja algfunktsioonide tabelist ja arvutab liitfunktsioonide tuletised diferentseerimisreeglite abil.
Tuletisfunktsiooni elementaarse arvutuse näide[muuda | muuda lähteteksti]
Otsitagu funktsiooni tuletist. Edasi arvutatakse muutude suhe:
- .
Nüüd leitakse piirprotsessis, kus , funktsiooni tuletis:
Diferentseerimisreeglid[muuda | muuda lähteteksti]
 Pikemalt artiklis Diferentseerimisreeglid
Pikemalt artiklis Diferentseerimisreeglid
Liirfunktsioonide, näiteks ja , diferentseerimine taandatakse diferentseerimisreeglite abil elementaarfunktsioonide diferentseerimisele (vaata ka Tuletiste ja algfunktsioonide tabel).
Järgnevate reeglitega saab liitfunktsioonide diferentseerimise taandada lihtsamata funktsioonide diferentseerimisele. Olgu , ja (oma määramispiirkonnas) diferentseeruvad reaalarvuliste argumendi väärtuste ja funktsiooni väärtustega funktsioonid ning ja reaalarvud. Siis kehtivad järgmised reeglid:
- Pöördfunktsiooni reegel
- Kui funktsioon on kohal diferentseeruv bijektiivne funktsioon, ning selle pöördfunktsioon on kohal diferentseeruv, siis
- Funktsiooni graafiku punkti peegeldamisel 1. nurgapoolitaja suhtes saadakse funktsiooni graafiku punkt ; funktsiooni graafiku tõus punktis on siis pöördväärtus funktsiooni graafiku tõusust punktis .
- Logaritmiline tuletis
- Liitfunktsiooni reeglist järeldub, et funktsiooni naturaallogaritmi tuletis
- .
- Murdu kujul nimetatakse logaritmiliseks tuletiseks.
- Astmefunktsiooni tuletis
- Funktsiooni diferentseerimiseks tuletame meelde, et reaalarvuliste astendajatega astmed defineeritakse eksponentsiaalfunktsiooni kaudu: . Liitfunktsiooni reegli ja korrutamisreegli abil saame:
- .
- Leibnizi reegel
- Kahe korda diferentseeruva funktsiooni ja -is tuletis saadakse valemist
- .
- Siin esinevad avaldised kujul on binomiaalkoefitsiendid.
- Faà di Bruno valem
- See valem väljendab kahe korda diferentseeruva funktsiooni kompositsiooni -indat tuletist. See valem üldistab liitfunktsiooni reegli mitmekordsetele tuletistele.
Mittediferentseeruvad funktsioonid[muuda | muuda lähteteksti]
Iga diferentseeruv funktsioon on pidev, ümberpöördu aga ei kehti. Veel 19. sajandi alguses oldi veendunud, et pidev funktsioon saab olla mittediferentseeruv mitte rohkem kui vähestel kohtadel (nagu absoluutväärtuse funktsioon). Bernard Bolzano konstrueeris esimesena funktsiooni, mis on kõikjal pidev, aga ei ole kuskil diferentseeruv, aga see ei saanud teistele matemaatikutele teatavaks. 1860ndatel leidis sellise funktsiooni ka Karl Weierstraß (Weierstraßi funktsioon) ja see lõi matemaatikute seas laineid. Pideva mittediferentseeruva funktsiooni tuntud mitmemõõtmeline näide on Kochi kõver, mille esitas 1904 Helge von Koch.
Mitte kõikjal diferentseeruva funktsiooni näide[muuda | muuda lähteteksti]
Funktsioon (absoluutväärtuse võtmine) ei ole kohal 0 diferentseeruv.
Tõepoolest, iga korral , mistõttu
- .
Seevastu iga korral ning järelikult
- .
Et vasakpoolne piirväärtus ja parempoolne piirväärtus ei lange kokku, siis piirväärtus ei eksisteeri. Seega ei ole funktsioon kohal 0 diferentseeruv. Sellegipoolest on see funktsioon diferentseeruv kõigil teistel kohtadel.
Kohal 0 eksisteerivad siiski parempoolne piirväärtus
ja vasakpoolne piirväärtus
- .
Funktsiooni graafiku järgi on näha, et diferentseeruvuse mõiste tähendab näitlikult, et funktsiooni graafik on nurkadeta.
Mitte kuskil diferentseeruva pideva funktsiooni näide[muuda | muuda lähteteksti]
Mitte kuskil diferentseeruvaid pidevaid funktsioone on esialgu raske ette kujutada, kuid nende näideteks on peaaegu kõik Wieneri protsessi (Browni liikumise) trajektoorid. Wieneri protsessi kasutatakse näiteks aktsiakursside graafikute modelleerimiseks.
Mitte kõikjal pidevalt diferentseeruva funktsiooni näide[muuda | muuda lähteteksti]

Funktsiooni nimetatakse pidevalt diferentseeruvaks, kui selle tuletis on pidev funktsioon. Isegi kui funktsioon on kõikjal diferentseeruv, ei pruugi tuletis olla pidev. Näiteks funktsioon
on diferentseeruv kõikjal, sealhulgas kohal . Tuletis, mille saab kohal 0 muutude suhte kaudu leida,
ei ole aga kohal 0 pidev.
Newtoni-Leibnizi valem[muuda | muuda lähteteksti]
 Pikemalt artiklis Newtoni-Leibnizi valem
Pikemalt artiklis Newtoni-Leibnizi valem
integreerimine ja diferentseeriine on omavahel seotud:
Kui on vahemik, pidev funktsioon ja suvaline punkt, siis on funktsioon
pidevalt diferentseeruv, ja selle tuletis on .
Sellega on antud juhatus integreerimiseks. Otsitakse funktsiooni, mille tuletis on integreeritav. Siis Newtoni-Leibnizi valem ütleb:
- .
Ajalugu[muuda | muuda lähteteksti]


Diferentsiaalarvutuse ülesandepüstitus oli antiigist saadik tuntud puutujaprobleemina. Üks lahenduskava nägi kõverjoone puutuja lähendamist joone lõikajaga lõplikult, aga suvaliselt väikeses vahemikus. Tuli ületada lõpmatu väikesele vahemikule ülemineku tehniline raskus.
Diferentsiaalarvutuse algmed pärinevad Pierre de Fermat'lt, kes töötas umbes 1628 välja meetodi algebraliste avaldiste ekstreemumite määramiseks ning koonuselõigete ja teiste kõverate puutujate arvutamiseks. Tema meetod oli puhtalgebraline, ta ei vaadelnud piirprotsesse ega tuletisi. Siiski saab tema meetodit tõlgendada matemaatilise analüüsi vahenditega ning on teada, et ta mõjutas Isaac Newtonit ja Gottfried Wilhelm Leibnizit.
Mõni aasta hiljem valis René Descartes teise algebralise meetodi, asetades kõvera juurde ringjoone, mis lõikab kõverat kahes lähestikku asetsevas punktis või puutub kõverat. See lähenemine võimaldas tal määrata teatud kõverate tõusud.
17. sajandi lõpus õnnestus Isaac Newtonil ja Gottfried Wilhelm Leibnizil töötada teineteisest sõltumatult välja vastuoludeta diferentsiaal- ja integraalarvutuse. Newton lähenes probleemile füüsikaliselt hetkkiiruse probleemi kaudu, Leibniz aga geomeetriliselt puutujaprobleemi kaudu. Nende tööd võimaldasid abstraheeruda puhtgeomeetrilisest esitusest ja seetõttu peetakse neid matemaatilise analüüsi alguseks.
Tuntuks said need eelkõige Guillaume François Antoine, markii de L'Hôpitali raamatu kaudu. De L'Hôpital õppis eraviisiliselt Johann Bernoulli juures ja avaldas tema matemaatilise analüüsi alased uurimused.
Tänapäeval tuntud diferentseerimisreeglid põhinevad eelkõige Leonhard Eulerilt, kes võttis kasutusele funktsiooni mõiste.
Newton ja Leibniz töötasid kui tahes väikeste positiivsete arvudega. Seda kritiseerisid ebaloogilisuse tõttu juba kaasaegsed, näiteks George Berkeley vaidluskirjas "The analyst; or, a discourse addressed to an infidel mathematician". Hoolimata valitsevast ebakindlusest arendati diferentsiaalarvutust järjekindlalt edasi, esmajoones selle arvukate rakenduste tõttu teistes matemaatika harudes ja füüsikas. Tollele ajale sümptomaatiline oli Kuningliku Preisi Teaduste Akadeemia auhinnatöö teema: "Kõrgem geomeetria kasutab sageli lõpmata suuri ja lõpmata väikesi suurusi; ometi vältisid antiikõpetlased hoolega lõpmatust, ja mõned meie aja kuulsad analüütikud tunnistavad, et sõnad "lõpmatu suurus" on vastuolulised. Akadeemia nõuab niisiis, et selgitataks, kuidas on vastuolulisest eeldusest tekkinud nii palju õigeid lauseid, ning et antaks kindel ja selge alusmõiste, mis võiks lõpmatuse asendada, tegemata arvutust liiga raskeks ega liiga pikaks; ..."[1]
Alles 19. sajandi alguses õnnestus Augustin-Louis Cauchyl anda diferentsiaalarvutusele tänapäevase ranguse, loobudes lõpmatu väikestest ja lõpmata suurtest suurustest ning defineerida tuletise lõikaja tõusude (muutude suhete) piirväärtusena. Tänapäeval kasutatava piirväärtuse definitsiooni võttis lõpuks kasutusele Karl Weierstraß 19. sajandi lõpus.
1822. aastal esitas Charles Babbage kuninglikule astronoomiaühingule ettekande «Märkusi masinate rakendamise kohta astronoomiliste ja matemaatiliste tabelite arvutamisel» ja tegi ettepaneku ehitada diferentsiaalarvustumasin. See oli mõeldud veatute matemaatiliste tabelite tootmise kiirendamiseks ning seda võib pidada tänapäevaste arvutite eellaseks. 1991. aastal valmis Londoni teadusmuuseumis sellise diferentsiaalarvustusmasina töötav eksponaat.[2]
Viited[muuda | muuda lähteteksti]
- ↑ Hans Wussing, Heinz-Wilhelm Alten, Heiko Wesemüller-Kock, Eberhard Zeidler. 6000 Jahre Mathematik: Von Euler bis zur Gegenwart, Springer-Verlag 2008, lk 233.
- ↑ Kilde tehnoloogiaajaloost
| Tsitaadid Vikitsitaatides: Diferentsiaalarvutus |