Fourier' teisendus
Fourier' teisendus (ka Fourier' pööre, inglise keeles Fourier transform) on integraalteisenduste hulka kuuluv lineaarne operaator, mis teisendab funktsiooni selle sagedusspektrit iseloomustavaks funktsiooniks . See teisendus põhineb teoreemil, mille kohaselt mistahes pidev ja piisavalt regulaarne funktsioon on esitatav siinusfunktsioonide integraalina. Fourier' teisendus on pööratav operatsioon. Enamasti on reaalarvuline ja kompleksarvuline, kus kompleksarv kirjeldab kindla sageduskomponendi faasi ja amplituudi.
Definitsioon
[muuda | muuda lähteteksti]Fourier' teisendust on võimalik defineerida mitmel viisil.[1][2] Antud artiklis kasutatakse definitsiooni:
- , iga reaalarvu ξ jaoks.
Kui argument x on aeg t (SI ühikuga sekund), siis teisenduse argument ξ esindab sagedust (hertsides). Sobivates tingimustes on funktsiooni kaudu võimalik avaldada ehk pöördteisendusega:
- iga reaalarvu x jaoks.
Asjaolu, et abil saab taastada funktsiooni , kutsutakse Fourier' pöördteoreemiks, mida tutvustati esmakordselt prantsuse füüsiku ja matemaatiku Joseph Fourier' artiklis "Analytical Theory of Heat"[3][4], ehkki see tõestati tänapäeva standardite järgi ära alles 1948. a.[5]. Muutujaid ja kutsutakse Fourier' integraalpaariks või Fourier' teisenduspaariks.
Fourier' teisendust eukleidilises ruumis vaadatakse eraldi juhuna, kus argument x esindab tihti asukohta ja ξ impulssi.

Sissejuhatus
[muuda | muuda lähteteksti]Fourier' teisendus tuleneb Fourier' rittaarendusest. Fourier' rittaarendus võimaldab kirjutada keerulisi, ent perioodilisi funktsioone siinuste ja koosinuste summana. Fourier' teisendus on Fourier' rea pikendus, kus vastava funktsiooni periood on venitatud lõpmatusse.[6]
Fourier' teisendus vastab Laplace'i teisendusele, kui selle juures lugeda kompleksmuutuja (argumendi) reaalosa võrdseks nulliga.
Näide
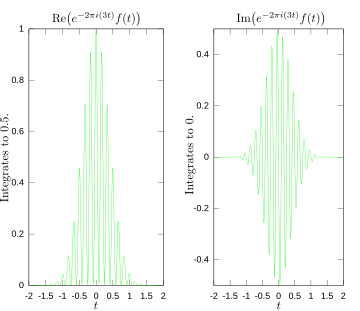
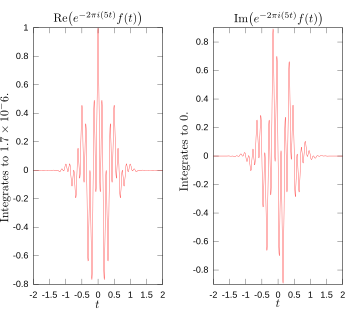
[muuda | muuda lähteteksti]Järgmised skeemid illustreerivad, kuidas Fourier' teisendus mõõdab, kas mingis funktsioonis esineb teatud sagedusi. Funktsioon f(t) = cos(6πt) e-πt2 võngub sagedusega 3 hertsi (kui t on sekundites) ja läheneb 0-le kiirelt. (Teine tegur võrrandis on ümbrisfunktsioon (funktsioon, mille kõver piirab laine amplituudide ekstreemumeid), mis vormib antud pideva sinusoidi lühikeseks impulsiks.) See funktsioon on spetsiaalselt valitud, et sellel oleks reaalne Fourier' teisendus, mida on lihtne graafiliselt esitada (vt esimest pilti). Selleks, et arvutada , tuleb integreerida e−2πi(3t)f(t). Teine pilt näitab selle funktsiooni reaalset ja imaginaarset osa. Reaalosa on pea alati positiivne, sest kui f(t) on negatiivne, on ka e−2πi(3t) reaalosa mittepositiivne. Tingituna sellest, et need võnguvad samal sagedusel, on e−2πi(3t) reaalosa positiivne, kui f(t) on mittenegatiivne. Reaalosa integreerimisel on tulemuseks suhteliselt suur number (antud juhul 0,5). Kui mõõta aga mõnd teist sagedust, mida vaadeldud sinusoidis ei esine, nagu näiteks funktsiooni puhul, võngub integreeritav osa piisavalt, et tulemus tuleks väike. Enamasti on olukord keerulisem, ent sisuliselt mõõdab Fourier' teisendus just niimoodi seda, kui palju spetsiifiline sagedus funktsioonis f(t) esineb.
-
Originaalfunktsioon, mis võngub sagedusel 3 hertsi
-
Fourier' teisenduse integraalialuse reaal- ja imaginaarosad sagedusel 3 hertsi
-
Fourier' teisenduse integraalialuse reaal- ja imaginaarosad sagedusel 5 hertsi
-
Fourier' teisendus, kus roheline täpp esindab 3 hertsi ja punane täpp 5 hertsi
Fourier' teisenduse omadused
[muuda | muuda lähteteksti]Eeldame, et f(x), g(x) ja h(x) on integreeritavad funktsioonid ja mõõdetavad reaalsirgel Lebesgue'i mõõduga ning rahuldavad järgmist valemit:
Nende funktsioonide Fourier' teisenduste tähistused on vastavalt , ja .
Alusomadused
[muuda | muuda lähteteksti]Fourier' teisendusel on järgmised alusomadused:[7]
- Lineaarsus
- Iga kompleksarvu a ja b korral, kui , siis
- 1. teisendamine
- Iga reaalarvu x0 korral, kui siis
- 2. teisendamine
- Iga reaalarvu ξ0 korral, kui siis
- Skaleerimine
- Iga nullist erineva reaalarvu a korral, kui , siis Olukord a = −1 põhjustab järgmise omaduse: kui , siis
- Kui siis
- Täpsemalt öeldes, kui on reaalne funktsioon, siis , ehk, on hermiitiline funktsioon.
- Juhul, kui f on puhtimaginaarne, siis
- Integreerimine
- Asendades definitsiooni, saame
Fourier' teisendus nullpunktis () võrdub funktsiooni integraaliga üle selle määramispiirkonna.
Perioodilisus ja pööratavus
[muuda | muuda lähteteksti]Sobivatel tingimustel saab funktsiooni taastada selle Fourier' teisendusest . Tähistame Fourier' teisenduse sümboliga nii et . Fourier' teisenduse kahekordne rakendamine teatud funktsioonidele pöörab funktsiooni ümber: Seda võib tõlgendada "aja pööramisena". Seega kui rakendada teatud funktsioonile Fourier' teisendust 4 korda: saab vana funktsiooni tagasi, mis tähendab, et Fourier' teisendus on neljaperioodiline. Samamoodi saab Fourier' pöördteisenduse, kui rakendada Fourier' pööret 3 korda: .
Niisiis võib defineerida paarsuse operaatori , ,mis inverteerib aega järgmiselt :
Need ei kehti iga funktsiooni korral, vaid kindlatel tingimustel, mille dikteerib Fourier' pöördteoreem.
Fourier' teisendus eukleidilises ruumis
[muuda | muuda lähteteksti]Fourier' teisendust võib rakendada n dimensioonis, mil teisenduse defineerimiseks on samuti erinevaid võimalusi. Üks integreeritava funktsiooni f(x) defineerimise viisidest on järgmine:
kus x ja ξ on n-dimensioonilised vektorid ja x · ξ on nende skalaarkorrutis. Skalaarkorrutis on mõnikord kirjutatud kujul .
Kõik eelnevas peatükis kirjeldatud Fourier' teisenduse omadused kehtivad ka n dimensiooni puhul.[8]
Määramatuse printsiip
[muuda | muuda lähteteksti]Mida kontsentreeritum f(x) on, seda laiem peab olema selle Fourier' teisendus . Teisisõnu, kui "pigistada" funktsiooni argumendiga x, siis selle Fourier' teisendus argumendiga ξ "venib välja". Pole võimalik korraga kontsentreerida funktsiooni ja selle Fourier' teisendust.
Seda omadust võib tõlgendada kui määramatuse printsiipi. Kui f(x) on integreeritav ja ruut-integreeritav funktsioon, siis ilma üldistuse vähenemiseta on normaliseeritud funktsiooni f(x) kuju järgmine:
Plancherelli teoreem[9] ütleb, et siis ka on normaliseeritud.
x = 0 ümbruse kontsentratsiooni kirjeldab dispersioon[7]:
Määramatuse terminites on tegemist |f(x)|2 teise momendiga nulli suhtes.
Määramatuse printsiip ütleb, et kui f(x) on absoluutselt pidev ning funktsioonid x·f(x) ja f′(x) on ruut-integreeritavad, siis
Võrdsus on võimalik vaid juhul, kui (seega ), kus σ > 0 on suvaline reaalarv ja C1 on selline, et f on L2-normaliseeritud[7]. Teisisõnu on f normaliseeritud Gaussi funktsioon varieeruvusega σ2, keskpunktiga 0, ja selle Fourier' teisendus on Gaussi funktsioon varieeruvusega σ−2.
Õigupoolest järeldub eelmainitud võrratusest, et:
iga x0, ξ0 ∈ R [10].
Rakendused
[muuda | muuda lähteteksti]
Diferentsiaalvõrrandite analüüs
[muuda | muuda lähteteksti]Fourier' teisendust ja veel üldisemat Laplace'i teisendust kasutatakse diferentsiaalvõrrandite lahendamiseks. Kui f(x) on diferentseeritav funktsioon, Fourier' teisendusega , siis selle funktsiooni tuletise Fourier' teisendus on . Selle abil saab teisendada diferentsiaalvõrrandid algebralisteks võrranditeks. See meetod toimib ainult probleemide puhul, mille määramispiirkonnaks on kogu reaaltelg. Üldistades Fourier' teisendust mitme muutujaga diferentsiaalvõrranditele määramispiirkonnaga Rn, saab ka neid lihtsustada algebralisteks võrranditeks.
Teised tähistused
[muuda | muuda lähteteksti]Fourier' pöörde teised tüüpilised tähistused on:
Elektroonikas kasutatakse ξ asemel tihti oomegat ω (nurksagedus), mõnikord märgitakse Fourier' teisendust kujul F(jω), kus j on imaginaarühik, et märkida suhet Laplace'i teisendusega. Samas esitatakse Fourier' teisendus vahel ka kujul F(2πf), et märkida sagedust hertsides.
Kompleksse funktsiooni paremaks tõlgendamiseks võib selle kahe reaalarvulise funktsiooni A(ξ) ja φ(ξ) kaudu esitada polaarkoordinaatides:
kus
on amplituud ja
on faas.
Eelnevast lähtudes võib pöördteisenduse kirjutada kujul:
mis on rekombinatsioon kõigist f(x) sageduse komponentidest. Iga komponent on kompleksne sinusoid kujuga e2πixξ mille amplituud on A(ξ) ja algne faasinurk (kohal x = 0) on φ(ξ).
Teised defineerimisviisid
[muuda | muuda lähteteksti]Fourier' teisenduse võib esitada ka nurksageduse kaudu: ω = 2πξ, mille ühik on radiaani sekundi kohta.
Asendus ξ = ω/(2π) eelolevatesse valemitesse annab järgmise kuju:
Sellisel juhul avaldub pöördteisendus järgmiselt:
Erinevalt selle artikli defineerimise tavadest, selliselt defineeritud Fourier' pööre ei ole enam unitaarne teisendus määramispiirkonnas L2(Rn). See tähendab, et vektorite sisekorrutis (eukleidilises ruumis skalaarkorrutis) ei ole invariantne. Fourier' teisenduse valemite vahel esineb ka vähem sümmeetriat.
Esineb ka tava jaotada tegur (2π)n võrdselt Fourier' teisenduse ja pöördteisenduse vahel:
Selline Fourier' pööre on jälle unitaarne teisendus määramispiirkonnas L2(Rn). Samuti on olemas sümmeetria teisenduste vahel.
| tavaline sagedus ξ (herts) | unitaarne |
|
|---|---|---|
| nurksagedus ω (rad/s) | mitteunitaarne |
|
| unitaarne |
|
Vaata ka
[muuda | muuda lähteteksti]Viited
[muuda | muuda lähteteksti]- ↑ Applications of Fourier Transforms to Generalized Functions | Rahman, Matiur (2011) | WIT Press, ISBN 1845645642.
- ↑ A Friendly Guide to Wavelets | Kaiser, Gerald (1994) | Birkhäuser, ISBN 0-8176-3711-7.
- ↑ Théorie Analytique de la Chaleur | Fourier, J. B. Joseph (1822) | Chez Firmin Didot, père et fils.
- ↑ The Analytical Theory of Heat | Fourier, J. B. Joseph; Freeman, Alexander, translator (1878) | The University Press.
- ↑ Introduction to the theory of Fourier integrals | Titchmarsh, E (1948) | Clarendon, ISBN 978-0-8284-0324-5.
- ↑ Advanced Engineering Mathematics: Volume 2 , Chapter 18: Fourier integrals and Fourier transforms | Taneja, HC (2008) | I. K. International Pvt Ltd, ISBN 8189866567.
- ↑ 7,0 7,1 7,2 7,3 Introduction to Fourier Analysis and Wavelets[alaline kõdulink] | Pinsky, Mark (2002) | Brooks/Cole, ISBN 0-534-37660-6.
- ↑ Introduction to Fourier Analysis on Euclidean Spaces | Stein, Elias; Weiss, Guido (1971) | Princeton University Press, ISBN 978-0-691-08078-9.
- ↑ "Plancherel's Theorem.", Weisstein, Eric W. "Plancherel's Theorem." From MathWorld–A Wolfram Web Resource.
- ↑ Fourier Analysis: An introduction | Stein, Elias; Shakarchi, Rami (2003) | Princeton University Press, ISBN 0-691-11384-X.




































![{\displaystyle {\mathcal {P}}[f]\colon t\mapsto f(-t),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbe49057a4072d0faa2a0e4b8046d81066e767db)


























