Geostatsionaarne orbiit
See artikkel vajab toimetamist. |
See artikkel ootab keeletoimetamist. |
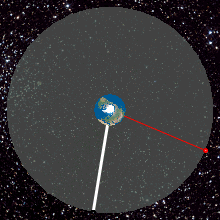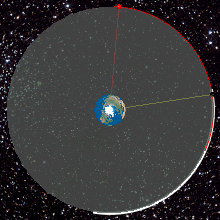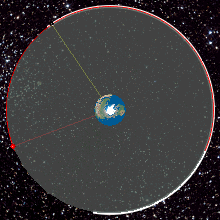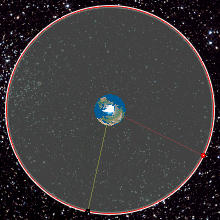


Geostatsionaarne orbiit, geostatsionaarne Maa orbiit või geosünkroonne ekvatoriaalne orbiit (GEO) on ringikujuline orbiit 35 786 kilomeetri kõrgusel, mis asetseb Maa ekvaatori kohal (0° laiuskraad), on kohakuti Maa pöörlemise suunaga ning mille ekstsentrilisus on ligidal nullile[1]. Objektil, mis on sellisel orbiidil, on orbitaalne periood võrdne Maa pöörlemise perioodiga (üks ööpäev) ja seetõttu tundub Maal olevatele vaatlejatele satelliit kindlas taevapunktis statsionaarselt olevana.
Kommunikatsioonisatelliidid ja ilmasatelliidid omavad tihti geostatsionaarseid orbiite, kuna satelliidi antennid, mis nendega suhtlevad, ei pea neid jälgima. Seetõttu on neid võimalik jälgida kogu aeg ning antenne saab suunata täpselt ühele kindlale positsioonile. Seda omadust kasutades on võimalik teha teaduseksperimente, näiteks ookeani värvi mõõtvad satelliidid (sh Geostationary Ocean Color Imager ehk GOCI), mida saab opereerida geostatsionaarsel orbiidil nii, et on võimalik jälgida väga väikseid muutusi ookeani keskkondades. Geostatsionaarne orbiit on üks alaliike geosünkroonsest orbiidist.
Idee geosünkroonse satelliidi kasutamiseks sides tõi esimesena välja 1928. aastal Herman Potočnik[2]. Esimene geostatsionaarse orbiidi kirjeldus populaarteaduslikus kirjanduses oli George O. Smith raamatus "Venus Equilateral", kus ei mindud veel väga detailidesse. Briti ulmekirjanik Arthur C. Clarke kirjutas geostatsionaarsetest orbiitidest põhjalikumalt 1945. aasta Wireless Worldi ajakirja väljaandes "Extra-Terrestial Relays – Can Rocket Stations Give Worldwide Radio Coverage?". Raamatu sissejuhatuses avaldas Clarke tunnustust ka George O. Smithi raamatule "The Complete Venus Equilateral"[3]. Clarke'i poolt esimesena kirjeldatud kasulikku kommunikatsiooni eesmärgil loodud orbiiti satelliitidele, tuntakse ka Clarke'i orbiidi nime all. Sarnaselt on ka defineeritud Clarke'i vöö, mis on piirkond kosmoses, 35 786 kilomeetri kõrgusel Maa keskmisest merepinna tasemest ja asub samal ajal ekvaatori tasandil, kus geostatsionaarsete orbiitide lähedased orbiidid on võimalikud[3]. Clarke'i orbiit on umbes 265 000 km pikk.
Praktilised kasutusalad[muuda | muuda lähteteksti]
Enamik kommerts-kommunikatsiooni satelliite, telekommunikatsioonisatelliite ja SBAS satelliite opereerivad geostatsionaarsetel orbiitidel. Geostatsionaarset ülemineku orbiiti kasutatakse, et asetada satelliit madalast Maa-lähedasest orbiidist geostatsionaarsele orbiidile (Vene televisiooni satelliidid on kasutanud ka elliptilisi Molniya ja Tundra orbiite kõrgete laiuskraadide tõttu, millel osa Venemaa elanikkonnast asub). Syncom-3 oli esimene satelliit, mis lennutati raketil Delta-D geostatsionaarsele orbiidile 1964. aastal.
Ülemaailmset satelliitide võrgustikku, mis koosneb meteoroloogistest satelliitidest ja mis asuvad geostatsionaarsel orbiidil, kasutatakse, et edastada nähtavas ja infrapunases piirkonnas tehtud pilte Maa pinnast ja atmosfäärist. Need satelliitide süsteemid on järgmised:
- Ameerika Ühendriikide GOES
- Meteosat, mille saatis üles Euroopa kosmoseagentuuri ja mida opereerib Euroopa ilmasatelliitide organisatsioon (European Weather Satellite Organization) ja ka EUMETSAT
- Jaapani MTSAT
- India INSAT seeria
Kasutades päikesepurje on teoreetiliselt võimalik orbiiti säilitada nii kaua kuni elektroonika radiatsiooni tõttu enam ei tööta. Seda ideed ei ole siiani rakendatud, kuid see idee on väga lootustandev.[viide?]
Orbiidi stabiilsus[muuda | muuda lähteteksti]
Geostatsionaarne orbiit on saavutatav ainult kõrgustel, mis on väga lähedased 35 786 km-ile, ning orbiitidel, mis on täpselt ekvaatori kohal. Sellel orbiidil on objektide kiirused 3,07 km/s ning orbiidi periood on 1436 minutit, mis on peaaegu täpselt võrdne ühe ööpäevaga ning võrdne 23,934461223 tunniga. See tagab, et satelliit on kooskõlas Maa pöörlemise perioodiga ning on Maalt vaadates statsionaarse jalajäljega. Kõik geostatsionaarsed satelliidid asuvad sellel ringil.
Kombinatsioon Kuu gravitatsioonist, Päikese gravitatsioonist ja Maa ellipsoididilisest kujust tähendab, et igal geostatsionaarsel objektil hakkab orbiidi tasand pretsesseerima. Selle pretsessiooni periood on umbes 53 aastat ning algne inklinatsiooni gradient, mis on umbes 0,85 kraadi aastas, viib selleni, et umbes 26,5 aasta järel on maksimaalne inklinatsioon 15 kraadi. Et seda orbitaalset häiritust korrigeerida on vajalikud regulaarsed orbitaalsed manöövrid, mille jaoks on satelliidile vaja anda aasta jooksul umbes 50 m/s suurune delta-v. Delta-v on kiirus, mida on vaja objektile anda, et orbiidi manöövrit teha.
Teine efekt, millega tuleb arvestada, on pikkuskraadide nihe, mida põhjustab Maa asümmeetrilisus, ehk teisisõnu on ekvaatori kuju vähesel määral elliptiline. Seetõttu on geostatsionaarsel orbiidil kaks stabiilset tasakaalupunkti, mis on 75,3°E ja 104,7°W, ning kaks mittestabiilset tasakaalupunkti, mis on 165,3°E ja 14,7°W. Suvaline geostatsionaarne objekt, mis asub nende kahe tasakaalupunkti vahel kiireneb aeglaselt stabiilsete tasakaalupunktide poole. Tulemuseks hakkab objekt perioodiliselt tasakaalupunkti ümber liikuma. Selle efekti korrigeerimiseks on vajalikud kontrollimanöövrid, mis vajavad kuni 2 m/s delta-v suurust mõjutust satelliidile. Vajaliku delta-v hulk sõltub ka soovitavast pikkuskraadist.
Päikesetuule ja radiatsiooni poolt tekitatav jõud avaldavad orbiidi stabiilsusele samuti mõju, mis ajapikku viivad geostatsionaarsel orbiidil oleva objekti selle algsest orbiidist eemale.
Kui satelliitidele ei viida Maa pealt kütust juurde või kui ei kasutata taastuvaid jõuallikaid, siis seab orbiidi stabiilsus kütuse tarbimise tõttu limiidi satelliidi eluajale sellel kindlal orbiidil.
Kommunikatsioonid[muuda | muuda lähteteksti]
Geostatsionaarsetel orbiitidel asuvad satelliidid on küllalt kaugel Maast, et tekitada märkimisväärne ajavahe signaali saatmise ja vastuvõtmise vahel. Umbes veerand sekundit läheb selleks, et üks Maal asuv saatja saadaks signaali satelliidile ja saaks vastuse maajaamalt. Ehk siis suhtluseks kahe maajaama vahel läheb pool sekundit aega.
Maajaamadele, mis on laiuskraadidel φ = ±45° satelliidi meridiaanist saab signaali liikumist Maalt satelliidile ja tagasi arvutada kasutades koosinusteoreemi. Selle jaoks peab olema antud geostatsionaarse orbiidi raadius r, Maa raadius R ning valguse kiirus c. Selle valemi saab välja kirjutada kui
Siin tuleks ka märkida, et r on orbitaalne raadius ehk kaugus Maa keskpunktist, mitte kaugus Maa pinnast.
See ajavahe tekitab probleeme süsteemides, kus on tähtis latentsus näiteks kommunikatsioonis[4].
Geostatsionaarsed satelliidid on täpselt ekvaatori kohal ja paistavad seetõttu madalamad, mida kaugemale põhja või lõunasse liikuda. Mida absoluutväärtuses suurem on laiuskraad, seda raskem on satelliidiga kommunikatsioone hoida. Seda põhjustab atmosfääris lainete murdumine, Maa soojuslik kiirgus, vaatevälja piiravad objektid (näiteks puud ja kõrgemad hooned) ning signaali peegeldused ligidal olevatest ehitistest või maalt. Alates 81° laiuskraadist ei ole võimalik enam geostatsionaarseid satelliite näha, sest nad vajuvad horisondi alla. Seetõttu ei saa ka geostatsionaarseid satelliite polaaraladel üldse kasutada[5].
Satelliitide orbiidil paiknemine[muuda | muuda lähteteksti]
Kõik satelliidid geostatsionaarsel orbiidil peavad asuma ühel ringil ekvaatori kohal. Kuna satelliitide kommunikatsioon ei tohi omavahel interfereeruda operatsioonide käigus, siis on sellel orbiidil piiratud arv "kohti", sest kommunikatsiooniks sobivad raadiosagedused on limiteeritud. Piirangute tõttu tekib ka konflikte riikide vahel, kes tahavad sarnaseid kohti orbiidil (probleemiks riikidel, mis asuvad samadel pikkuskraadidel, aga erinevatel laiuskraadidel) ning tahavad jaotada satelliitide sagedusi. Sageduste jaotamiste ja nendega seotud probleemidega tegeleb Rahvusvaheline Telekommunikatsiooni Liit.
1976. aasta Bogota deklaratsioonis proovisid kaheksa riiki ekvaatoril kuulutada nende kohal oleva kosmoseala enda territooriumiks, kuid sellega ei oldud rahul teiste riikide poolt. Nüüdseks tegeleb taoliste teemade lahendamisega Rahvusvaheline Telekommunikatsiooni Liit.
Piirangud satelliitide elueale[muuda | muuda lähteteksti]
Kui satelliitidel saab kütus otsa, siis ei suuda need enam püsida geostatsionaarsel orbiidil. Tavaliselt saatjad ja ülejäänud satelliidil asuvad alamsüsteemid kestavad kauem kui kütus ning teatud hulka satelliite on seetõttu võimalik kasutada ka osaliselt inklineeritud orbiitidel, kus on maajaamade poolt tagatud korralik satelliitide jälgimissüsteem. Kui satelliidid on oma eluea lõpus, siis liiguvad need geostatsionaarselt orbiidilt surnuaia orbiidile, kus ei seata ohtu uutele satelliitidele, mis tulevikus üles lastakse. Nii välditakse töötavate satelliitide kokkupõrkeid kakosmoseprügiga[6][7].
Geostatsionaarse kõrguse tuletus[muuda | muuda lähteteksti]
Igal ringikujulisel orbiidil on vajalik kesktõmbe jõud (Fc). See jõud on Maa orbiidil antud Maa gravitatsiooni poolt ja tähistatakse (Fg)-ga. Et arvutada geostatsionaarse orbiidi kõrgust on vaja kõigepealt kirja panna seos:
Newtoni teise seaduse abil saame me asendada jõud F objekti massi ja kiirenduse korrutisega:
Seejärel asendame valemis kiirenduse Maa gravitatsioonilise konstandiga:
Siin tuleb tähele panna, et mass 'm' on nii vasakul kui ka paremal pool avaldises.See tähendab, et kõrguse arvutamine lihtsustub selle punkti leidmisele, kus kesktõmbekiirendus on võrdne gravitatsiooni poolt tekitatava kiirenduse 'g'-ga.
Kesktõmbekiirenduse magnituud on antud järgmise valemiga:
kus ω on nurkkiirus ning r on orbiidi raadius mõõdetuna Maa massikeskmest.
Gravitatsiooni poolt tekitatud kiirenduse magnituud on antud järgmise valemiga:
kus M on Maa mass, 5,9736 × 1024 kg, ning G on gravitatsiooniline konstant 6,67428 ± 0,00067 × 10−11 m3 kg−1 s−2.
Kahe võrduse kokku panemisel saame järgmise avaldise:
Korrutis GM on tuntud palju täpsemalt kui kumbki tegur eraldi ning seetõttu antakse sellele eraldi väärtus ja tähis μ = 398 600,4418 ± 0,0008 km3 s−2. Sellega avaldatud valem näeb välja järgmiselt:
Nurkkiirus on leitav, kui jagada nurk, mis on läbitud ühes täis pöördes orbitaalse perioodiga (aeg, mil satelliit teeb ühe täis pöörde Maa ümber). Geostatsionaarse orbiidi korral on orbitaalseks perioodiks üks ööpäev ehk 86164,09054 sekundit. See annab:
Seejärel on võimalik eelmise valemiga välja arvutada orbiidi raadius, mis annab vastuseks 42 164 kilomeetrit. Lahutades Maa ekvatoriaalse raadiuse, 6378 kilomeetrit, on geostatsionaarse orbiidi kõrguseks 35 786 kilomeetrit.
Satelliidi kiirus ehk kiirus mida satelliit peab omama, et sellel orbiidil püsida on võimalik arvutada korrutades nurkkiirus orbiidi raadiusega:
Sama valemiga saame arvutada ka teiste planeetide geostatsionaarseid orbiite. Marsil on geotsentriline gravitatsiooni konstant GM 42828 km3s−2 ning Marsi pöörlemise periood (T) on 88642,66 sekundit. Kuna ω = 2π/T, siis saame ω väärtuseks 7,088218×10−5 s−1. Saame tulemuseks, et r3 = 8,5243×1012 km3, mille kuupjuur on 20 427 km; ning lahutades Marsi ekvatoriaalse raadiuse (3396,2 km) saame, et Marsi korral on orbiidi kõrguseks 17 031 km.
Vaata ka[muuda | muuda lähteteksti]
Viited[muuda | muuda lähteteksti]
- ↑ A geostationary Earth orbit satellite model using Easy Java Simulation Loo Kang Wee and Giam Hwee Goh 2013 Phys. Educ. 48 72
- ↑ Noordung, Hermann (1995) [1929]. The Problem With Space Travel. Translation from original German. DIANE Publishing. Lk 72. ISBN 978-0-7881-1849-4.
- ↑ 3,0 3,1 "Extra-Terrestrial Relays — Can Rocket Stations Give Worldwide Radio Coverage?" (PDF). Arthur C. Clark. Oktoober 1945. Originaali arhiivikoopia (PDF) seisuga 18. märts 2009. Vaadatud 4. märtsil 2009.
- ↑ The Teledesic Network: Using Low-Earth-Orbit Satellites to Provide Broadband, Wireless, Real-Time Internet Access Worldwide
- ↑ p. 123
- ↑ Shi Hu-Li, Han Yan-Ben, Ma Li-Hua, Pei Jun, Yin Zhi-Qiang and Ji Hai-Fu (2010). Beyond Life-Cycle Utilization of Geostationary Communication Satellites in End-of-Life, Satellite Communications, Nazzareno Diodato (Ed.), ISBN 978-953-307-135-0, InTech, "Beyond Life-Cycle Utilization of Geostationary Communication Satellites in End-of-Life".[alaline kõdulink]
- ↑ "Inclined orbit operation".







![{\displaystyle r^{3}={\frac {GM}{\omega ^{2}}}\to r={\sqrt[{3}]{\frac {GM}{\omega ^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/180afe4e9da7670c6baa5db2fb06811a0469cb02)
![{\displaystyle r={\sqrt[{3}]{\frac {\mu }{\omega ^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86fc9c7797f74da609ad17740a92d557e33af69e)

