Märgumine

Veetilgad puitu märgamas

Märgumine on pinnanähtus, mille korral vedelik jääb molekulaarjõudude tõttu tahkise pinnaga ühendusse ehk valgub laiali. See tuleneb molekulidevahelisest interaktsioonist, kui vedelik ja pind kokku saavad. Märgumise ulatus sõltub adhesiooni- ja kohesioonijõu vastastikuseist suhteist.

Kui märgumine toimub näiteks vee ja klaasi vahel, siis mittemärgumine esineb näiteks elavhõbedakuulikese liikumisel mööda põrandat. Sel juhul ületab elavhõbedakuuli kohesioonijõud põranda ja kuulikese vahelise adhesioonijõu.

Märgumine on tähtis omadus, mis iseloomustab kahe materjali kleepuvust või nendevahelist sidet. Märgumine ja pinnajõud põhjustavad lisaks märgumisele teisigi nähtusi, sealhulgas kapillaarnähtusi. Hoolimata märgumise ulatusest, on vedelikutilga kuju tahkel pinnal umbes kera segmendi kujuga.

Seletus

Adhesioonijõud, mis esinevad vedeliku ja tahkise vahel, põhjustavad vedelikutilga levimist üle pinna. Kohesioonijõud vedeliku sees põhjustavad vedelikutilga kerakujuliseks muutumist ja pinnaga kontakti hoidmist.

Joonis 1. Veetilk ideaalsel pinnal

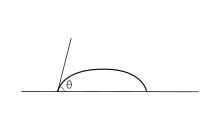
Märgumisnurk (nagu näha joonisel 1) on nurk, mille all vedeliku ja gaasi piirpind on kontaktis tahkise ja vedeliku piirpinnaga. Märgumisnurk on määratud adhesiooni ja kohesioonijõududega. Kui tilga kalduvus valguda laiali mööda tahket siledat pinda suureneb, väheneb märgumisnurk. Seega märgumisnurk on pöördvõrdeline märgavusega.

Märgumisnurka, mis on väiksem kui 90°, nimetatakse väikeseks. See näitab tavaliselt, et pinna märgumine on soodustatud ja et vedelik voolab üle suure pinna laiali. Märgumisnurka, mis on suurem kui 90°, nimetatakse suureks. See näitab tavaliselt, et pinna märgumist ei toimu ja vedelik minimeerib kontakti pinnaga, moodustades kompaktseid vedelikutilgakesi.

Käsitledes vett, võib märguvat pinda nimetada hüdrofiilseks ja mittemärguvat pinda hüdrofoobseks. Superhüdrofoobse pinna märgumisnurk on suurem kui 150°, mille tõttu on vedeliku ja pinna vahel peaaegu olematu kontakt. Seda nähtust kutsutakse lootose efektiks. Vedelike jaoks, mis ei ole vesi, kasutatakse terminit lüofiilne väikese märgumisnurga jaoks ja lüofoobne suure märgumisnurga jaoks.

Joonis 2. Erinevate vedelike märgumine tahkel pinnal. A kujutab vedelikku, mis märgab pinda vähe. B kujutab vedelikku, mis märgab pinda keskmiselt. C kujutab vedelikku, mis märgab pinda ulatuslikult. S tähistab tahket pinda

Pinnaenergia

On kahte tüüpi pindasid, millega vedelikud saavad vastastikku toimida. Tahked pinnad on jaotatud kõrge ja madala energiaga pindadeks.

Tahkised, näiteks metallid, klaasid ja keraamika on tuntud kui "kõvad tahkised". Sidemetüübid, mis neid koos hoiavad (nt kovalentsed ja metallilised sidemed), on väga tugevad. Nende lõhkumiseks on vaja palju energiat, järelikult on nad kõrge energiaga. Enamik molekulaarseid vedelikke märgavad selliseid tahkiseid täielikult.

Teine tahkistetüüp on madala energiaga tahkised, mille molekulide vahel on nõrgad sidemed (nt Van der Waalsi jõud ja vesiniksidemed). Kuna need on väga nõrgad, kuluks nende lõhkumiseks väga vähe energiat, järelikult on nad madala energiaga tahkised. Olenevalt vedelikust võimaldavad madala energiaga pinnad kas täielikku või osalist märgamist.

Laialivalgumistöö

Laialivalgumistöö suurus määrab tilga kuju tahkise pinnal. Kui keha kattub vedelikukihiga, on laialivalgumistöö süsteemi energiamuut.

Kui vedelikutilk panna pinnale ja ta hakkab laiali valguma, siis tahkise- ja gaasifaasi vaheline pindala väheneb, tahkise- ja vedelikufaasi ning vedeliku- ja gaasifaasi vaheline pindala hakkab kasvama.

Kui vaadelda süsteemi tahkis-vedelik-gaas, siis vedelik valgub laiali, kui

s_TV + s_VG – s_TG < 0, kus

s_TV – tahkise ja vedeliku vaheline pindpinevus,

s_VG – vedeliku ja gaasi vaheline pindpinevus,

s_TG – tahkise ja gaasi vaheline pindpinevus.

Antud võrrand kehtib ka vedeliku laialivalgumisel teisel vedelikul, juhul kui nad üksteises ei lahustu.

Ideaalsed tahked pinnad

Ideaalne tahke pind on lame, jäik, täielikult sile, keemiliselt homogeenne ega oma märgumisnurga hüstereesi. Lisaks võtab vedelikutilk pinnal oma esialgse kuju, kui teda häirida. Järgnevad lähendused kehtivad vaid ideaalsete pindade korral.

Joonis 3. Kolm vedelikufaasi piirpindadega. α, β ja θ on vastavad nurgad piirpindade vahel

Energia miinimumi printsiip, kolm faasi

Vaatleme süsteemi, mis koosneb kolmest vedelikust. Joonis 3 kujutab joont, kus kolm faasi kokku puutuvad. Tasakaalulised olekus on kogujõud pikkusühiku kohta kolme faasi piirpinnal võrdne nulliga. Kogujõu komponendid igal piirpinnal on antud kui:

γ_αθ + γ_θβ cos θ + γ_αβ cos α = 0

γ_αθ cos θ + γ_θβ + γ_αβ cos β = 0

γ_αθ cos α + γ_θβ cos β + γ_αβ = 0, kus

α, β ja θ on joonisel näidatud nurgad ja γ_ij on pinnaenergia kahe faasi i ja j vahel. Neid suhteid saab kujutada ka kolmnurgana. See on tuntud kui Neumanni kolmnurk, mis on kujutatud joonisel 4. Neumanni kolmnurk allub kolmnurga omadusele α + β + θ = 2π ning siinuse ja koosinusega opereerimise reeglitele.

Joonis 4. Neumanni kolmnurk. See kujutab joonisel 3 oleva kolme vedela faasi, mis eksisteerivad staatilises tasakaalus, pinnaenergiaid ja faasidevahelisi nurki

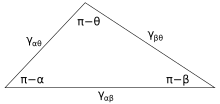
Kuna kolm pinnaenergiat moodustavad kolmnurga küljed, alluvad nad valemile γ_ij < γ_jk + γ_ik. See tähendab, et ükski pindpinevus ei tohi ületada teise kahe summat. Kui kolm vedelikku, mis ei allu nendele piirangutele, tuuakse kontakti, ei saa tekkida tasakaalu. Sel juhul tekib vedelikkude segunemine.

Youngi võrrand

Kui faas nurgaga β vahetatakse sileda jäiga pinna vastu (näidatud joonisel 5), siis β = π ja teine jõud taandub Youngi võrrandiks:

γ_TG = γ_TV + γ_VG cos θ , kus

γ_TG – pinnaenergia tahkise- ja gaasifaasi vahel,

γ_TV – pinnaenergia tahkise- ja vedelikufaasi vahel,

γ_VG – pinnaenergia vedeliku ja gaasifaasi vahel.

See iseloomustab pindpinevust kolme faasi vahel: vedelik, tahkis ja gaas. See kehtib ka olukorras, kus gaasi asemel on teine vedelik, milles esimene, tilga kujul esinev vedelik, ei lahustu.

Joonis 5. Vedelikutilga märgumisnurk jäiga tahkise pinnal

Reaalsed siledad pinnad ja Youngi märgumisnurk

Youngi võrrand eeldab täielikult siledat ja jäika pinda. Paljudel juhtudel aga ei ole pinnad ligelähedaseltki ideaalsed. Probleemile saab läheneda kahel viisil: pind on kare (mitteideaalne kare jäik pind) või pind on sile, kuid siiski reaalne (lõplikult jäigad pinnad). Isegi täielikult siledal pinnal võib märgumisnurgal olla mitmesuguseid väärtusi alates maksimaalsest θ_A kuni minimaalse märgumisnurgani θ_R. Tasakaalulise märgumisnurga θ_C saab arvutada θ_A ja θ_R abil:

$\theta _{\mathrm {c} }=\arccos \left({\frac {r_{\mathrm {A} }\cos {\theta _{\mathrm {A} }}+r_{\mathrm {R} }\cos {\theta _{\mathrm {R} }}}{r_{\mathrm {A} }+r_{\mathrm {R} }}}\right)$ ,

kus

$r_{\mathrm {A} }=\left({\frac {\sin ^{3}{\theta _{\mathrm {A} }}}{2-3\cos {\theta _{\mathrm {A} }}+\cos ^{3}{\theta _{\mathrm {A} }}}}\right)^{1/3}~;~~r_{\mathrm {R} }=\left({\frac {\sin ^{3}{\theta _{\mathrm {R} }}}{2-3\cos {\theta _{\mathrm {R} }}+\cos ^{3}{\theta _{\mathrm {R} }}}}\right)^{1/3}$

Youngi-Dupré võrrand ja märgumiskoefitsient

Youngi-Dupré võrrand ütleb, et ei γ_TG ega γ_TV või olla suuremad kui teise kahe pinnaenergia summa. Sellest võib järeldada, et täielik märgumine toimub, kui täidetud on tingimus γ_TG > γ_TV + γ_LG, ja märgumist ei toimu, kui täidetud on tingimus γ_TV > γ_TG + γ_VG. Kasulik parameeter märgumise uurimiseks on märgumisparameeter S, kus

S = γ_TG – (γ_TV + γ_VG).

Kui S > 0, siis vedelik märgab pinna täielikult. Kui S < 0, siis toimub osaline märgamine. Kombineerides märgumisparameetri definitsiooni Youngi lähendusega, saab Youngi-Dupré võrrandi:

S = γ_VG (cos θ – 1)

Selle järgi omab θ vaid siis füüsikalisi lahendeid, kui S < 0 .

Mitteideaalsed karedad pinnad

Erinevalt ideaalsetest ei ole mitteideaalsed pinnad täiuslikult siledad, jäigad ega keemiliselt homogeensed. Sellised kõrvalekalded ideaalsusest tingivad nähtuse, mida kutsutakse märgumisnurga hüstereesiks. Märgumisnurga hüsterees on defineeritud maksimaalse ja minimaalse märgumisnurga vahena:

H = θ_A – θ_R.

Mitteideaalse pinna maksimaalne märgumisnurk on maksimaalne stabiilne märgumisnurk ja minimaalne märgumisnurk on minimaalne stabiilne märgumisnurk. Märgumisnurga hüsterees eksisteerib sellepärast, et on olemas mitu termodünaamiliselt stabiilset märgumisnurka. Need varieeruvad termodünaamiliselt stabiilsed märgumisnurgad on tuntud metastabiilsete olekutena.

Levinud kõrvalekalduvus ideaalsusest on kare pind. Kare pind võib olla nii homogeene kui heterogeenne. Homogeense pinna korral täidab vedelik kareda pinna ebatasasused. Heterogeense pinna korral märgab vedelik mitut laadi karedusi. Sellistel pindadel on märgamisele mitmesugune mõju. Cassie-Baxteri ja Wenzeli mudel on kaks peamist mudelit, millega tekstuuriga pindade märgumist kirjeldatakse. Need kehtivad vaid siis, kui vedelikutilga suurus on palju suurem märjatava pinna kareduseastmest.

Wenzeli mudel

Joonis 6. Wenzeli mudel

Wenzeli mudel kirjeldab homogeenset märgamist ja seda on kujutatud joonisel 6. See mudel defineerib märgumisnurga karedal pinnal:

cos θ* = r cos θ,

kus θ* on nähtav märgumisnurk, mis on vastavuses stabiilse tasakaalulise olekuga, ehk süsteemi olek minimaalse vabaenergiaga. r on kareduse määr.

θ on Youngi märgumisnurk, mis on defineeritud ideaalsel pinnal.

Cassie-Baxteri mudel

Joonis 7. Cassie–Baxteri mudel

Heterogeense märgamise korral ei ole Wenzeli mudel enam piisav. Cassie-Baxteri võrrand on järgmine:

cos θ*= r_f f cos θ_Y + f – 1,

Kus r on karedus märgunud pinnal ja f on märjatud ala tahkel pinnal. On oluline tähele panna, et kui r_f = r ja f = 1, muutub Cassie-Baxteri võrrand Wenzeli võrrandiks.

Pindaktiivsete ainete mõju pinna märgumisele

Paljud tehnoloogilised protsessid nõuavad kontrolli vedeliku märgamise üle tahkel pinnal. Tilga asetamisel pinnale võib see pinna märjata täielikult, osaliselt või üldse mitte. Pindaktiivsete ainete abil saab vähendada pindpinevust ja muuta mittemärgava aine osaliselt või täielikult märgavaks.

Pindaktiivse aine segunedes vedelikuga tahkise- ja gaasifaasi piirpind suureneb ning tilga ääred muutuvad hüdrofiilseteks. Selle tulemusena tilk levib.

Vaata ka

• Adsorptsioon
• Üleslükkejõud
• Märgamine
• Kapillaarsus