Doppleri efekt
Doppleri efekt on füüsikaline nähtus, mis avaldub selles, et helilaine või elektromagnetlaine registreeritav (tajutav, mõõdetav) sagedus sõltub lainete allika ja vastuvõtja liikumise kiirusest ja suunast. Kui allikas ja vastuvõtja lähenevad teineteisele, siis sagedus suureneb, teineteisest eemaldumisel sagedus väheneb. Sageduse suurenemine on samaväärne lainepikkuse vähenemisega ja vastupidi.[1]
Kõige sagedasem näide Doppleri efektist on sõiduki signaali helikõrguse muutus, kui sõiduk algul läheneb vaatlejale ning hiljem eemaldub vaatlejast. Võrreldes väljuva sagedusega on vastuvõetud sagedus suurem, kui sõiduk läheneb vaatlejale, identne sellega, kui sõiduk on otse vaatleja kõrval ning madalam, kui sõiduk eemaldub vaatlejast.[2]
Doppleri efekti põhjuseks on asjaolu, et kui lainete allikas liigub vaatleja suunas, siis iga üksik laine, mis järjest tekitatakse, on eelmisega võrreldes vaatlejale lähemal. Seega iga laine võtab pisut vähem aega, et jõuda vaatlejani kui sellele eelnev laine, mistõttu kahe järjestikuse lainefrondi jõudmine vaatlejani on kiirem (lainefrontide omavaheline kaugus on vähenenud) ning selle tulemusena sagedus kasvab. Lained on "kokku surutud".[2][3] Kui aga laineallikas liigub vaatlejast eemale, siis iga järgnev laine lähtub pisut kaugemalt kui eelnev laine. Seega kahe järjestikuse laine kohalejõudmise aeg on suurenenud mistõttu sagedus väheneb. Kahe järjestikuse lainefrondi vaheline kaugus suureneb. Lained on "välja venitatud".
Akustilise Doppleri efekti korral on määravaks nii heli allika kui ka vastuvõtja kiirus keskkonna suhtes. Optilise Doppleri efekti korral on määrav ainult allika ja vastuvõtja liikumise suhteline kiirus.
Heli ja elektromagnetkiirguse sageduse sõltuvust vastuvõtja ja heli- või kiirgusallika liikumise kiirusest põhjendas teoreetiliselt Austria füüsik Christian Doppler 1842. aastal.
Üldine valem
[muuda | muuda lähteteksti]Klassikalises füüsikas, kus allika ja vastuvõtja kiirused keskkonna suhtes on väiksemad kui lainete levimise kiirus keskkonnas, avaldub seos vaadeldava (vastuvõetava) sageduse ja allika poolt kiiratud sageduse vahel kujul[4]
- ,
kus
- on lainete levimise kiirus keskkonnas;
- – vastuvõtja kiirus keskkonna suhtes; positiivne, kui vastuvõtja liigub allika suunas, ning negatiivne, kui vastassuunas;
- – allika kiirus keskkonna suhtes; positiivne, kui allikas liigub eemale vastuvõtjast ning negatiivne, kui teises suunas.
Valem kehtib eeldusel, et allikas liigub sirgjooneliselt otse vaatleja suunas. Sagedus väheneb, kui kumbki (allikas või vastuvõtja) liigub teisest eemale.
Kui kiirused ja on väikesed võrreldes laine enda kiirusega, siis on seos vaadeldava sageduse ja kiiratud sageduse vahel esitatav ligikaudselt valemiga
ja sageduse muutus
- ;
nendes valemites ning .
Akustiline Doppleri efekt
[muuda | muuda lähteteksti]
Liikuva heliallika ja liikuva vastuvõtja korral kirjeldab helisageduse muutumist üldjuhul valem
- ,
kus on vastuvõetava (kuuldava) heli sagedus ja heliallika sagedus; on vastuvõtja liikumiskiirus ja allika liikumiskiirus; on heli levimiskiirus (normaaltingimustel).
Ülemine tehtemärk kehtib heliallikate teineteisele lähenemise korral ja alumine eemaldumisel. Kui heliallikas seisab paigal, siis ja kui heliallikas liigub paigalseisva vastuvõtja suhtes, siis .
Vaatleme lähemalt juhtu, kui heliallikas läheneb paigalseisvale vastuvõtjale. Sel juhul saame kirjutada arvutusvalemi kujul
- .
Kui näiteks operatiivauto, mille sisselülitatud sireeni sagedus Hz, läheneb paigalseisvale inimesele (vastuvõtjale) kiirusega 90 km/h ehk 90000/60·60 = 25 m/s, siis kuuleb inimene heli sagedusega
- .
Füüsikaliselt võib tooni kõrgenemist vaadeldud näite andmeil seletada järgmiselt. Sireeni sagedusel 1000 Hz järgnevad õhuvõnkumise laineharjad üksteisele 1/1000 sekundi järel, kusjuures lainepikkus
- .
Nii on see seisva sõiduki korral. Kui sõiduk liigub vastuvõtja poole kiirusega = 25 m/s, siis laineharjade vahe lüheneb ja vastuvõtjani jõuavad lained pikkusega
- .
Sellele lainepikkusele vastab sagedus
- ,
mis on sireeni sagedusest kõrgem.
Samamoodi saab arvutada ja seletada sireeni tooni madaldumist, kui allikas vastuvõtjast eemaldub. Vaadeldaval juhul
- .
Esitatud arvutused kehtivad eeldusel, et heliallika liikumised toimuvad otse vastuvõtja poole või sellest eemale. Sel juhul väheneb (ja suureneb) allika kaugus vastuvõtjast ühtlaselt ning üleminek kõrgemalt toonilt madalamale on järsk. Enamasti möödub signaaliallikas vastuvõtjast teatud kauguselt. Sellisel üldjuhul kirjeldab Doppleri nihet paigalseisva vastuvõtja suhtes valem
kus on signaaliallika kiirus ja on ajast sõltuv ühikvektor, mis on suunatud signaali allikast vastuvõtja poole.
Teatud kauguselt möödumisel muutub heliallika ja vastuvõtja vahekaugus ebaühtlaselt ja seetõttu toimub ka üleminek kõrgemalt toonilt madalamale sujuvalt.
Optiline Doppleri efekt
[muuda | muuda lähteteksti]Elektromagnetlained levivad ka vaakumis, seega ei vaja nad levimiseks keskkonda (nagu helilained). Kuid kui laineallikas liigub vastuvõtja (jälgija) suhtes, ilmneb samuti sageduste nihe. See relativistlik Doppleri efekt on seletatav sellega, et lained levivad lõpliku, absoluutse kiirusega, milleks on valguse kiirus . Sageduse muutus sõltub ainult allika ja vastuvõtja suhtelisest kiirusest ; kas seejuures liigub allikas, vastuvõtja või mõlemad, ei mõjuta see sageduse muutumist.
Relatiivsusprintsiibi kohaselt võib iga vaatlejat käsitleda paigalseisvana. Küll aga tuleb Doppleri efekti arvutamisel arvesse võtta vaatleja poole liikuvate lainete relativistlikku ajalist aeglustumist (ingl time dilation). Siis saab arvutada relativistliku Doppleri pikiefekti:
Elektromagnetlainete liikumisel vaatesuunaga risti ilmneb Doppleri ristefekt. See efekt on aga pikiefektist palju väiksem (mõjutab sagedust vähem) ja on sellega võrreldav üksnes väga suurel kiirusel.
Vaatamata sellele, et Doppleri efekti ja astronoomilise punanihke mõjud on sarnased (vaadeldava tähe või galaktika elektromagnetkiirguse sageduse vähenemine), ei või neid nähtusi segi ajada, sest neil on erisugused põhjused. Relativistlik Doppleri efekt on sagedusmuutuse peamine mõjutaja siis, kui lainete saatja ja vastuvõtja aegruumis liiguvad ning nende vahekaugus on suhteliselt väike ja seega nendevahelise ruumi paisumine veel mõju ei avalda. Alates teatud vahekaugusest saavutab ülekaalu aegruumi enda paisumise mõju sagedusele, nii et Doppleri efekti toime võib jätta arvesse võtmata.
Doppleri efekti rakendusi
[muuda | muuda lähteteksti]- Doppleri radar arvutab objekti lähenemise kiiruse lähtudes elektromagnetlainete sageduse muutusest saadetud ja peegeldunud signaalide vahel.
- Meteoroloogias mõõdetakse Doppleri radari abil keeristormide pöörlemisliikumisi.
- Õhuseires kasutatakse Doppleri efektil põhinevaid passiivradareid.
- Kiiruskaamerad kasutavad samuti Doppleri laserit.
- Vooliste (vedelike, gaaside) kiirust saab kontaktivabalt mõõta laseranemomeetriga, mis kasutab akustilist või optilist Doppleri efekti voolava aine hajusatel osakestel või mullidel.
- Meditsiinis kasutatakse akustilist Doppleri efekti ultraheliuuringutel verevoolu kiiruse mõõtmiseks.
- Muusikas rakendatakse Doppleri efekti kõlaefektide loomiseks, näiteks pöörleva Leslie kõlari abil.
Astronoomia
[muuda | muuda lähteteksti]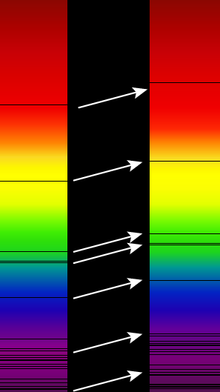
Astronoomias mõõdetakse Doppleri efekti abil tähtede ja galaktikate radiaalkiirusi ehk lähenemist või eemaldumist meist, mis avaldub vastavalt sininihke või punanihkena. Nii on võimalik mõõta ka galaktikate ja tähtede pöörlemist, avastada eksoplaneete.[6]
Punanihet kasutatakse ka kosmose paisumise uurimisel kuigi see pole otseselt Doppleri efekt.[7]
Kosmose paisumisel tekkivat punanihet on tihti kutsutud kosmoloogiliseks punanihkeks. Seda saab tuletada üldrelatiivsusteooria formalismi Robertsoni-Walkeri meetrikast. Astronoomias Doppleri efekt sõltub meie teadmistest tähtede mittehomogeense spektri kohta. Tekivad neeldumisjooned hästi defineeritud sagedustel, mis korreleeruvad energiaga, mida on vaja, et ergastada elektrone mitmetes elementides ühelt elektronkihilt teisele. Doppleri efekt on ära tuntav, kuna neeldumisjooned pole alati nendel sagedustel, mida annaks välja statsionaarne valgusallikas.
Kuna sinine valgus omab kõrgemat sagedust kui punane valgus, siis läheneva astronoomilise valgusallika spektrijooned kutsuvad esile sininihke ning kaugenev astronoomiline valgusallikas vastavalt punanihke.
Lähimate tähtedega suurimad radiaalkiirused Päikese suhtes on +308 km/s (BD- 4041, mida teatakse ka LHS 52 nime all) ning –260 km/s (Woolley 9722, mida teatakse ka Wolf 1106 ja LHS 64). Positiivne radiaalkiirus tähendab, et täht liigub Päikesest eemale, negatiivne seevastu, et täht läheneb Päikesele.
Vaata ka
[muuda | muuda lähteteksti]Viited
[muuda | muuda lähteteksti]- ↑ Doppleri efekti teoreetiline taust
- ↑ 2,0 2,1 "Possel, Markus (2017). "Waves, motion and frequency: the Doppler effect". Einstein Online, Vol. 5. Max Planck Institute for Gravitational Physics, Potsdam, Germany. Retrieved September 4, 2017.
- ↑ Henderson, Tom (2017). "The Doppler Effect – Lesson 3, Waves". Physics tutorial. The Physics Classroom. Retrieved September 4, 2017.
- ↑ Rosen, Joe; Gothard, Lisa Quinn (2009). Encyclopedia of Physical Science. Infobase Publishing. lk. 155. ISBN 0-8160-7011-3.
- ↑ https://commons.wikimedia.org/wiki/File:Redshift.png
- ↑ http://www.astro.ucla.edu/~wright/doppler.htm
- ↑ Harrison, Edward Robert (2000). Cosmology: The Science of the Universe (2nd ed.). Cambridge University Press. pp. 306ff. ISBN 0-521-66148-X.































