RC-filter
RC-filter (ingl k resistor-capacitor filter) on elektriline sagedusfilter, mis on koostatud sobiva takistite ja kondensaatorite lülituse kujul, ning on ette nähtud elektrilise signaali spektrit muutma või kujundama või välja jätma soovimatuid sageduskomponente ja edastama ainult valitud signaali sageduskomponente. Teisisõnu filtreerib see välja kõik soovimatud sagedused. Ideaalne filter eraldab ning edastab sinusoidseid sisendsignaale nende sageduste põhjal.
Madalsageduslikes rakendustes (kuni 100 kHz) kasutatakse peamiselt lihtsaid RC-ahelaid. RC-filter kuulub passiivfiltrite hulka. Passiivfiltrid on filtrid, mis koostatakse passiivsetest komponentidest, nagu näiteks takisti, kondensaator ja induktiivpool, ning neil puuduvad signaali võimendavad elemendid (näiteks transistor, operatsioonvõimendi). Seetõttu on passiivfiltreid läbivad signaalid väljundis üldjuhul väiksema amplituudiga kui sisendis.
Filtritele pannakse nimetus vastavalt sellele, millist signaalivahemikku need edastada lasevad, samal ajal blokeerides ülejäänud. Kõige sagedamini kasutatavad kolm filtrite tüüpi on:
- Madalpääsfilter, mis laseb läbi ainult mahalõikesagedusest (ingl k cutoff frequency, fc) väiksema sagedusega signaale ja blokeerib suuremad sagedused.
- Kõrgpääsfilter, mis laseb läbi ainult mahalõikesagedusest suurema sagedusega signaale ja blokeerib väiksemad sagedused.
- Ribapääsfilter, mis laseb läbi mingile kindlale signaalivahemikule vastavad signaalid ja blokeerib sellest vahemikust kõrgemad ja madalamad sagedused.
Ideaalsed filtrid[muuda | muuda lähteteksti]
Ideaalne madalpääsfilter lõikab täielikult maha kõik sagedused, mis jäävad mahalõikesagedusest ülespoole, samal ajal pääsevad madalamad sagedused läbi muutumatul kujul. Kõrgpääsfiltri puhul on täpselt vastupidi, lõigatakse maha kõik mahalõikesagedusest väiksema sagedusega signaalid. Ribapääsfilter võib olla lihtne kombinatsioon eelnevast kahest, kus mõlema filtri mahalõikesagedust sättides eraldatakse soovitud sageduste vahemik. Kõigil juhtudel on sageduse graafik sarnane ristküliku kujuga, kus pärast mahalõikesagedust on signaali amplituud nullilähedane. Ideaalsel filtril puudub niisiis üleminekuala, mille jooksul filtri amplituudsageduskarakteristik langeb. Ideaalsed filtrid ei ole realiseeritavad.
Reaalsed filtrid[muuda | muuda lähteteksti]
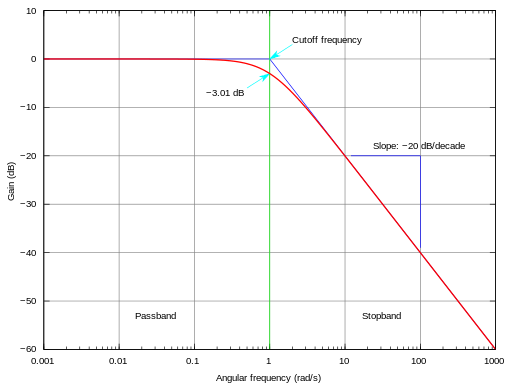
Reaalse filtri puhul ei ole signaali amplituud pärast mahalõikesagedust kohe nullilähedane, vaid hakkab vähenema pöördvõrdeliselt sagedusega. Logaritmilisel sageduskarakteristikul vastab sellele lineaarne asümptootiline langus. Sellepärast ei ole mahalõikesagedus defineeritud sageduskarakteristiku punkti järgi, kust signaali amplituud hakkab vähenema (mida rangelt võttes olemas ei ole), vaid hoopis sagedusest, kus kondensaatori mahtuvustakistus ja takisti takistus on võrdsed. Sagedusel, kus see juhtub, on väljundisse jõudva signaali amplituud langenud 70,7% (1/√2) tasemele sisendsignaali omast. Teisisõnu on väljundisse jõudev signaal sisendsignaalist detsibellide skaalas −3 dB. Kuna skeem sisaldab kondensaatorit, tekib reaalse filtri puhul ka faasinihe ehk hilistus sisendi ja väljundi vahel, mis on põhjustatud kondensaatori näivtakistuse reaktiivsest iseloomust. Faasinihke suurust näitab faasinurk φ, mis sõltub sagedusest. Suuremate sageduste puhul on faasinihe suurem ja lõikesagdusel jõuab 45 kraadini. Kui kondensaatori impedants käituks sedasi, et teatud sagedusest suuremate sageduste korral on see lõpmatu suur ja väiksemate sageduste korral on impedants 0 oomi lähedal, oleks ideaalsed filtrid võimalikud. Tegelikult on kondensaatori impedants esitatav aga valemiga
- ,
kus Zc on kompleksimpedants oomides, ω (oomega) on nurksagedus radiaanides sekundis, C on kondensaatori mahtuvus faradites ja j on kompleksarv. Üleval oleva valemit kasutades saadakse RC-sagedusfiltri amplituud-sagedus-karakteristik. Ülal paremal oleval graafikul on see toodud täislogaritmilises skaalas.
Madalpääsfilter[muuda | muuda lähteteksti]

Definitsiooni järgi on madalpääsfilter skeem, mis võimaldab väikeste sageduste läbipääsu ja takistab suurte sageduste läbipääsu. RC-madalpääsfilter koosneb takistist, millega koormus on jadamisi, ja kondensaatorist, mis on koormusega rööbiti. Kondensaatoril on reaktiivtakistus, mis on suur madala sagedusega signaalide jaoks, sundides neid liikuma läbi koormuse. Suurematel sagedustel kondensaatori mahtuvustakistus väheneb ja kondensaator hakkab paremini juhtima, shuntides nii koormust suurema sagedusega signaalide jaoks. Takistuse ja mahtuvuse korrutis annab filtri ajakonstandi[1] . Mahalõikesageduse fc määrab ära seesama ajakonstant. Sageduse fc (hertsides) leidmiseks kehtib
- ,
kus fc on lõikesagedus Hertsides, τ on ajakonstant sekundites, R on takistus oomides, ja C on mahtuvus faradites.
Või võrdväärselt nurksageduse (ühikuks radiaane sekundis) kehtib
- .
Veel üks viis, kuidas skeemi tööpõhimõtet mõista, on keskenduda ajale, mis kulub kondensaatori laadimisele.
- Madalatel sagedustel on piisavalt aega selleks, et pinge kondensaatori otstel jõuaks kaasas käia signaali muutumise kiirusega, mis tähendab, et mingit signaali moonutust ei esine.
- Suurtel sagedustel toimub kondensaatori laadumine või tühjenemine liiga aeglaselt. Signaal muutub palju kiiremini, kui pinge kondensaatori otstel. Sedasi silutakse suuremad sagedused lihtsalt välja, sest väljundpinget võetakse kondensaatori pealt.
Kõrgpääsfilter[muuda | muuda lähteteksti]
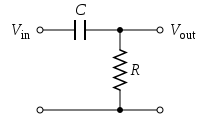
Kõrgpääsfilter toimib madalpääsufiltrile täpselt vastupidi: see pakub suurte sagedustega signaalidele kerget läbipääsu ja teeb madalate sagedustega signaalide läbipääsu raskeks. RC-kõrgpääsfilter koosneb kondensaatorist, millega koormus on jadamisi, ja takistist, mis on koormusega rööbiti. Tööpõhimõte on väga sarnane madalpääsfiltriga (mahalõikesageduse arvutamise valem on mõlemal filtril täpselt sama). Erinevus seisneb selles, et madalpääsfiltri puhul on kondensaator koormusega rööbiti ja madalatel sagedustel on kondensaatori takistus suur, mis surub signaali väljundisse. Nüüd on kondensaator jadamisi signaali teel ees ja kuna kondensaatori takistus on pöördvõrdeline sagedusega, ei pääse signaal sealt läbi. Mõlemast filtri võib mõelda ka kui pingejagurist, kus kondensaatorit võib teatud reservatsioonidega käsitleda kui tavalist muudetava takistusega takistit (potentsiomeetrit). Antud võrdlusega on võimalik uurida, kuidas muutub väljundpinge erinevate takistuste suhete korral.
Ribapääsfilter[muuda | muuda lähteteksti]
Teatud rakendustes on vaja, et läbi pääseks ainult kindlas sageduste vahemikus asuvad signaalid ja muude sagedustega signaalid summutatakse ära. Suhteliselt laiaribalisi ribapääsfiltreid saab realiseerida madalpääsfiltreid ja kõrgpääsfiltreid omavahel kombineerides. RC-ribapääsfilter on kooslus madalpääsfiltrist ja kõrgpääsfiltrist, kus madalpääsfilter eraldab soovitud vahemikust kõrgemad sagedused ja kõrgpääsfilter eraldab soovitud vahemikust madalamad sagedused. Tänu nende kahe filtri koostööle jääb alles soovitud sagedusvahemik. Kuna kondensaatorite impedants on sagedusest sõltuv, siis nagu kõrval olevalt graafikult näha, ei ole ka siin mahalõikesagedus defineeritud punktist, kust signaali amplituud muutuma hakkab. See on hoopis defineeritud selle punkti järgi, kus väljundisse jõudva signaali amplituud on langenud −3 dB tasemele sisendisse tuleva signaali suhtes. Probleem selliste ribapääsfiltrite lahendustega on see, et signaal peab alati läbima kahte filtrit ja need koos võivad nõrgestada signaali amplituudi rohkem kui ainult üks filter.
Raadiotehnilised ribafiltrid on enamasti realiseeritud LC-ahelatena.
Rakendused[muuda | muuda lähteteksti]
Heli[muuda | muuda lähteteksti]
Kõrgpääsfiltreid kasutatakse helitehnikas, kus muusikast eraldatakse välja kõrged sagedused ja suunatakse saadud heli kõrgsageduskõlarisse, samal ajal summutades madalaid sagedusi, mis võivad kõlarile kahju teha. Madalpääsfiltriga tehakse täpselt vastupidist: summutatakse suured sagedused ja madalad sagedused edastatakse bassikõlarile. Ribapääsfiltreid rakendatakse kesksageduskõlarite tarvis. Kuna inimene ei kuule helisid madalamalt kui 20 Hz, filtreeritakse võimenditesse minevast muusikast välja väiksemad sagedused. Seda põhimõtet rakendatakse ka sageduste puhul, mis on suuremad kui 20 kHz. Kõrgpääsfiltrit kasutatakse ka alalisvoolu (sagedus 0 Hz) eraldamiseks signaalist, mis võib vähendada võimendi kasutegurit ja genereerida üleliigset sooja kõlari mähises.
Pilditöötlus[muuda | muuda lähteteksti]
Kõrgpääsfiltreid ja madalpääsfiltreid kasutatakse ka pilditöötluses, kus nende abil on võimalik töödelda ja täiendada pilte, vähendada müra jm.
Muud rakendused[muuda | muuda lähteteksti]
Alalisvoolu toiteplokkides kasutatakse madalpääsfiltreid selleks, et eraldada alalisvoolust vahelduvvool.
Viited[muuda | muuda lähteteksti]
- ↑ Sedra, Adel; Smith, Kenneth C. (1991). Microelectronic Circuits, 3 ed. Saunders College Publishing. Lk 60. ISBN 0-03-051648-X.





