Sagedusfilter

Sagedusfilter on elektriahel või elektroonikalülitus signaalide eristamiseks, läbilaskmiseks või tõkestamiseks sagedusliku tunnuse alusel. Vastavalt sellele on filtri amplituudi-sageduse tunnusjoonel ehk sageduskarakteristikul eristatavad pääsuala ning tõkkeala ja nende vahel siirdeala.

Liigitus filtri sageduskarakteristiku iseloomu järgi

Ideaalset filtrit läbivad pääsualasse kuuluvate sagedustega signaalid või signaalide komponendid nõrgenemata (sumbumata) ja tõkkealasse kuuluvate sagedustega signaalid tõkestatakse täielikult.

Erinevalt ideaalsest filtrist pole reaalse filtri ülekandetegur sama kogu pääsualas ja tõkkevõime pole täielik, samuti jääb pääsu- ja tõkkeala vahele sageduskarakteristiku siirdeala (näiteks madalpääsfiltris f_p kuni f_t). Eriti selgelt on see märgatav analoogsignaalide töötlemiseks mõeldud lihtsamate, madalat järku filtrite puhul.

Madalpääsfiltri amplituudi-sageduse tunnusjooned:
a ‒ ideaalne tunnusjoon; b ‒ reaalne tunnusjoon; c ‒ lõikesagedus f_l

Ribapääsfiltri ja ribatõkkefiltri sagedustunnusjoon

Selle järgi, milliseid sagedusi filter läbi laseb või tõkestab, liigitatakse filtreid järgmiselt:

• madalpääsfilter, millel on pääsuala sagedusvahemikus nullist kuni teatud sageduseni f_p ja tõkkeala sagedusest f_t kuni lõpmatuseni;
• kõrgpääsfilter, millel on pääsuala sagedusest f_p kuni lõpmatuseni ja tõkkeala sagedusvahemikus nullist kuni teatud sageduseni f_t;
• ribapääsfilter (lühemalt: ribafilter), millel on pääsuala sagedusvahemikus f_‒p kuni f_+p ning tõkkeala sagedusest 0 kuni f_‒t ja f_+t kuni lõpmatuseni;
• ribatõkkefilter (lühemalt: tõkkefilter), millel on tõkkeala sagedusvahemikus f_‒t kuni f_+t ning pääsuala sagedusest 0 kuni f_‒p ja f_+p kuni lõpmatuseni.

Sagedusfiltriteks võib lugeda ka sageduskäiku korrigeerivaid lülitusi, näiteks [[Vinüülplaadimängija #RIAA-kõverad |RIAA-filter].

Paljud tehnikas kasutatavad filtrid ei vasta kuigi hästi sellisele üldisele lihtsustatud liigitusele. Selliste filtrite näideteks võiksid olla analoogteleviisorites kasutatavad videosignaali vahesagedusvõimendid-filtrid ja mitmesugused helitehnikas kasutatavad korrektorfiltrid (näiteks RIAA sageduskorrektor).

Liigitus ülekandefunktsiooni järgi

Filtrite jaoks, mis on teostatud elektriahelate või elektroonikalülituste kujul, saab leida nende poolt realiseeritava ülekandefunktsiooni (mis seob lülituse väljundsuurust sisendsuurusega operaatorkujul) ja sellele vastava sageduskarakteristiku kompleksmuutuja polünoomide suhtena. On olemas mitmesuguseid polünoome niisuguse sageduskarakteristiku saamiseks, mis nõutava täpsusega aproksimeerib soovitavat amplituudi-sageduse karakteristikut, s.t on sellele piisavalt lähedane. Selleks kasutatavate polünoomide autorite järgi nimetatakse ka filtritüüpe. Nii tuntakse Butterworthi, Tšebõšovi, Caueri, Besseli ja Gaussi filtreid. (Vene matemaatiku Tšebõšovi nimi esineb eestikeelsetes tekstides ka kujul Tšebõšev, samuti kirjutatakse teistes keeltes nime mitut moodi.)

Butterworthi filter

Butterworthi filtri sagedustunnusjooned

Butterworthi madalpääsfiltri amplituudi-sageduse karakteristikut väljendab seos

${\frac {U_{v}}{U_{s}}}={\frac {1}{\sqrt {1+\left({\frac {f}{f_{l}}}\right)^{2n}}}},$

kus

$U_{v}$ on filtri väljundpinge;

$U_{s}$ ‒ filtri sisendpinge;

$f_{l}$ ‒ lõikesagedus, s.o sagedus, millel väljundpinge on langenud tasemeni ${\frac {1}{\sqrt {2}}}\approx 0{,}7071$ sisendpingest (detsibellides: 20 * log( 0,7071 ) = ‒3,01 dB, ehk ümardatult 3 detsibelli võrra);

$n$ ‒ filtri järk, millest sõltub sagedustunnusjoone kalle siirdealas: iga järguga suureneb sageduskarakteristiku asümptootiline kalle 6 dB võrra oktaavi kohta (sageduste suhe 2 : 1) või vastavalt 20 dB dekaadi kohta (sageduste suhe 10 : 1); koos järguga kasvab ka filtri lülitusskeemi keerukus.

Filtri amplituudi-sageduse tunnusjoon on pääsualas suures ulatuses rõhtne. Filtri sumbealas, mis hõlmab siirde- ja tõkkeala, on tunnusjoone kalle 6n dB/oktav.

Filtri faasi-sageduse karakteristik on teataval määral ebalineaarne, mis põhjustab signaali siirdemoonutust, eriti kõrgemat järku filtrites; see avaldub siseneva pingeastangu korral väljundpinge ülevõnkena, mis kiiresti sumbub.

Tšebõšovi filter

Tšebõšovi filtri sagedustunnusjooned (a) ja sumbumuse muutumine pääsualas, kui lainjus a_p on 2 dB (b)

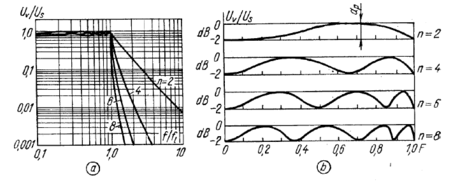
Tšebõšovi madalpääsfiltri amplituudi-sageduse karakteristik avaldub kujul

${\frac {U_{v}}{U_{s}}}={\frac {1}{\sqrt {1+\varepsilon ^{2}T_{n}^{2}(F)}}},$

kus

$U_{v}$ on filtri väljundpinge;

$U_{s}$ ‒ filtri sisendpinge;

$\varepsilon ={\sqrt {10^{\frac {a_{p}}{10}}-1}}$ ‒ konstant, mille väärtuse määrab tunnusjoone etteantud lainjus $a_{p}$ pääsualas (valitaksre tavaliselt vahemikus 0,1 ‒ 3 dB);

$T_{n}(F)$ ‒ Tšebõsovi polünoom, mis on suhtelise sageduse $F={\frac {f}{f_{p}}}$ funktsioon, sõltudes filtri järgust ($f_{p}$ on pääsuala piirsagedus).

Pääsualas on filtri sagedustunnusjoon laineline, kusjuures lainete arv kasvab koos filtri järguga. Pääsuala piirsagedusel, kus F = 1, on filtri sumbumus võrdne lainjusega a_p. Piirsageduse järel langeb sagedustunnusjoon järsemalt kui sama järku Butterworthi filtril; langus on seda järsem, mida suurem on lubatav lainjus.

Vaadeldud 1. tüüpi Tšebõšovi filtri kõrval on võimalik konstrueerida ka 2. tüüpi filtrit ehk Tšebõšovi pöördfiltrit, millel sagedustunnusjoon on laineline tõkkealas, pääsualas aga sile (nagu Butterworthi filtril).

Faasi-sageduse tunnusjoon on Tšebõšovi filtril ebalineaarsem kui Butterworthi filtril; see väljendub siirdetunnusjoone suuremas ülevõnkes.

Caueri filter ehk elliptiline filter

Caueri filtri tunnusjooned sõltuvalt filtri järgust n

Caueri (Saksa matemaatiku Wilhelm Caueri järgi) madalpääsfiltri amplituudi-sageduse karakteristik on avaldatav kujul

${\frac {U_{v}}{U_{s}}}={1 \over {\sqrt {1+\varepsilon ^{2}R_{n}^{2}(\xi ,{\frac {f}{f_{p}}})}}},$

kus

$U_{v}$ on filtri väljundpinge;

$U_{s}$ ‒ filtri sisendpinge;

$\varepsilon$ ‒ sagedustunnusjoone lainjust väljendav parameeter;

$R_{n}(\xi ,{\frac {f}{f_{p}}})$ ‒ n järku ratsionaalne elliptiline funktsioon ($\xi$ on filtri tundlikkust mõjutav parameeter ja ${\frac {f}{f_{p}}}$ ‒ suhteline sagedus piirsagedus suhtes).

Nendel filtritel on sagedustunnusjoon laineline nii pääsu- kui ka sumbealas. Pääsualas muutub filtri väljundpinge sõltuvalt filtri järgust samamoodi kui Tšebõšovi filtri korral. Tõkkealas on lainjuskõveral sagedusi, kus väljundpinge langeb nullini, s.o sumbumus saavutab lõpmata suure väärtuse.

Pääsuala piirsageduse $f_{p}$ järel langeb sagedustunnusjoon järsult, seega on siirdeala tunduvalt kitsam kui eelvaadeldud filtreil. Ent Caueri filtri faasikarakteristik on veelgi ebalineaarsem kui sama järku Tšebõšovi filtril.

Besseli filter

Kui on vajalik, et filter võimalikult vähe moonutaks teda läbivate signaaliimpulsside kuju, peab filtri faasi-sageduse tunnusjoon olema võimalikult lähedane sirgjoonele. Ideaalse, s.o lineaarse faasikarakteristiku korral jõuavad kõik signaali eri sagedusega komponendid filtri väljundisse ühesuguse hilinemisega, seega samaaegselt. Sellele nõudele vastab kõige paremini filter, mille ülekandefunktsiooni formeerimiseks kasutatakse Saksa teadlase Friedrich Besseli polünoome. Sellist Besseli filtrit tuntakse ka Thompsoni filtrina.

Besseli filtri faasi-sageduse tunnusjooned sõltuvalt järgust

Besseli madalpääsfiltri ülekandefunktsioon:

${\frac {U_{v}}{U_{s}}}={\frac {1}{1+\sum _{i=1}^{n}c_{i}^{\prime }P^{i}}},$

kus

$U_{v}$ on filtri väljundpinge;

$U_{s}$ ‒ filtri sisendpinge;

$n$ ‒ filtri järk;

$P=\mathrm {j} {\frac {f}{f_{p}}}$ ($f_{p}$ on piirsagedus)

$c_{i}^{\prime }={\frac {2(n-i+1)}{i(2n-i+1)}}\cdot c_{i-1}^{\prime }.$

Besseli filtri amplituudi-sageduse tunnusjooned on laugemad kui Butterworthi filtril ja ei muutu oluliselt järsemaks ka filtri järgu suurendamisel üle 6‒8.

Gaussi filter

Ristkülikimpulss (sinise punktiiriga) muundub Gaussi filtrit läbides kellukese kujuliseks impulsiks

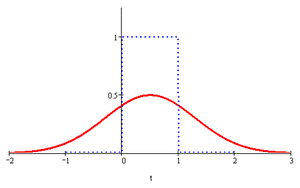
Gaussi filter on ribapääsfilter, millel on kellukakujuline sagedustunnusjoon ja minimaalne grupihilistus nii pääsu- kui tõkkealas. Filtri ülekandefunktsioon väljendab Gaussi jaotust (normaaljaotust):

${\frac {U_{v}}{U_{s}}}=e^{-\left({\frac {\omega }{2\alpha }}\right)^{2}},$

kus konstant $\alpha ={\frac {\pi }{\sqrt {\ln({\sqrt {2}})}}}.$

Gaussi filtrit kasutatakse näiteks modulatsioonitehnikas ristkülikimpulsside silumiseks, et vähendada edastamiseks vajalikku ribalaiust.

Passiiv- ja aktiivfiltrid

Sagedusfiltrid koostatakse induktiiv-mahtuvuslikest ehk LC-ahelatest ja ka takistus-mahtuvuslikest ehk RC-ahelatest. Et takistid, induktiivpoolid ja kondensaatorid on passiivsed elektroonikakomponendid, nimetatakse neist koostatud filtreid passiivfiltriteks.

Filtri mõõtmete vähendamiseks kasutatakse sageli RC-ahelaid. Takistites tekkiva signaalikao kompenseerimiseks lisatakse lülitusse aktiivelemendid, milleks on harilikult operatsioonvõimendid. Niisuguseid aktiivfiltreid nimetatakse ka ARC-filtriteks.

LC-aktiivfiltrites võib kogukat induktiivpooli asendada güraator ‒ operatsioonvõimendil põhinev impedantsimuundur.

Digitaalfiltrid

Digitaalse sagedusfiltri talitlus põhineb digitaalsel signaalitöötlusel. Analoogfiltritele omaste passiiv- ja aktiivkomponentide (kondensaatorid, poolid, operatsioonvõimendid) asemel kasutatakse peamiselt digitaalseid signaaliprotsessoreid, mis on programmeeritud signaalile vajalike sagedusomaduste andmiseks. Tarbe korral lisatakse neile analoog-digitaalmuundureid ja digitaal-analoogmuundureid.

Digitaalfiltrite eriomadusi.

• Võimalik on saada kuitahes järsu kaldega sagedustunnusjoont, näiteks luua madalpääsfiltri, mis laseb nõrgendamata läbi sagedused kuni 1000 Hz ja tõkestab täielikult sagedused, mis ületavad 1010 Hz. Mõistagi on realiseeritavad kõik analoogfiltrite puhul käsitletud ülekandefunktsioonid.
• Digitaalfiltri sagedusparameetrid on täpselt seadistatavad ja püsivad stabiilseina (erinevalt analoogfiltrite komponentide omadustest).
• Faasi-sageduse karakteristik on täiesti lineaarne.
• Iseloomulik on suur hilistumine, mistõttu nende kasutamisel reaalajas toimivate seadmete puhul tekib probleeme (näiteks meditsiinitehnika seadmetes).

Tulenevalt digiteerimise spetsiifikast, et moonutuste vältimiseks peab näiduvõtusagedus (diskreetimissagedus) vähemalt kahekordselt ületama signaali kõrgeima sageduskomponenti, vajavad digitaalfiltrisse antavad impulss-signaalid eelnevat silumist (kõrgeimate sageduste äralõikamist, nt Gaussi filtri abil). Samal põhjusel on piiratud digitaalfiltrite kasutamine kõrgetel raadiosagedustel, sest praeguste signaaliprotsessorite ja analoog-digitaalmuundurite sageduspiir jääb alla 100 MHz. Seepärast selekteeritakse raadiotehnilistes seadmetes (näiteks raadioside vahenditesm telerites ja raadiotes) sisendsignaale endiselt analooglülitustega.

Filtrite dimesioneerimine

Sagedusfiltrite praktiliseks dimensioneerimiseks on kasutada mitmesuguseid käsiraamatuid, tabeleid ja tarkvarapakette, sealhulgas vabavaralisi programme.

Vaata ka

• RC-filter
• Silufilter
• Pinnalainefilter
• Digitaalne filter

Kirjandus

• Lembit Abo. Raadiolülitused. Valgus, 1990, lk 13‒52.
• Arthur Bernard Williams, Fred J. Taylor. Electronic filter design handbook : LC, active and digital filters. McGraw-Hill, 1988, 816 p.
• Rudolf Saal, Walter Entenmann. Handbook of Filter Design. Dr. Alfred Hüthig Verlag, 1988, 799 p.