Normaaljaotus

Normaaljaotuseks (ka Gaussi jaotuseks) nimetatakse matemaatikas pideva juhusliku suuruse X jaotust, mida iseloomustab tihedusfunktsioon[1]
kus
- on keskväärtus, mis iseloomustab kõige suurema tõenäosusega esinevat suurust (normaaljaotusel sama väärtusega ka aritmeetiline keskmine, mediaan ja mood);
- on standardhälve, mis iseloomustab, kui palju juhuslikud suurused keskväärtusest erinevad. Normaaljaotuse tihedusfunktsiooni nimetatakse ka Gaussi funktsiooniks ja selle graafikut Gaussi kõveraks.
Normaaljaotuse eriline tähtsus tuleneb tsentraalsest piirteoreemist, mille kohaselt suure arvu sõltumatute muutujate liitmisel, on nõrkadel eeldustel saadud jaotus ligilähedaselt normaaljaotus.
Paljude mõõtmistulemuste hälbeid keskmisest saab loodus-, majandus- ja tehnikateadustes kas täpselt või väga heas lähenduses kirjeldada normaaljaotuse (bioloogias sageli logaritmilise normaaljaotuse) abil. See on nii eeskätt olukordades, kus paljud faktorid mõjuvad üksteisest sõltumatult eri suundades.
Näiteid
[muuda | muuda lähteteksti]
Normaaljaotusega juhusikke suurusi kasutatakse näiteks järgmiste nähtuste kirjeldamisel:
- juhuslikud mõõtevead
- juhuslikud hälbed etteantud mõõtmest detailide valmistamisel
- Browni liikumine.
Kindlustusmatemaatikas sobib normaaljaotus kahjuandmete modelleerimiseks keskmise suurusega kahjude korral.
Mõõtetehnikas kasutatakse sageli normaaljaotust, mis kirjeldab mõõtevigade hajumist.
Standardhälve
[muuda | muuda lähteteksti]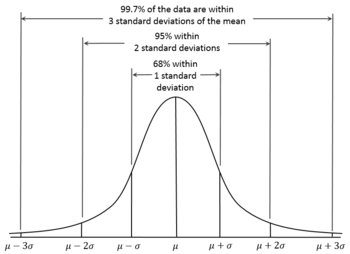
Standardhälve kirjeldab normaaljaotuse laiust. Normaaljaotuse poollaius on umbes 2,4-kordne (täpselt -kordne) standardhälve. Ligilähedaselt kehtib:
- hälbe vahemikus keskväärtusest paikneb 68,27% kõigist mõõtetulemustest;
- hälbe vahemikus keskväärtusest paikneb 95,45% kõigist mõõtetulemustest;
- hälbe vahemikus keskväärtusest paikneb 99,73% kõigist mõõtetulemustest;
Ja ümberpöördult saab antud tõenäosuste jaoks leida maksimaalsed hälbed keskväärtusest:
- 50%-l kõigist mõõtetulemustest on hälve keskmisest kuni ;
- 90%-l kõigist mõõtetulemustest on hälve keskmisest kuni ;
- 95%-l kõigist mõõtetulemustest on hälve keskmisest kuni ;
- 99%-l kõigist mõõtetulemustest on hälve keskmisest kuni .
Nii saab peale keskmise ka standardhälbele lihtsa tähenduse omistada.











