Difraktsioon



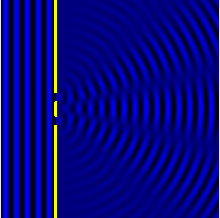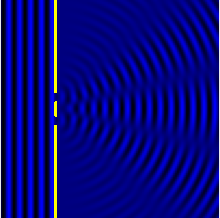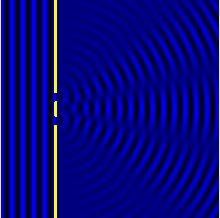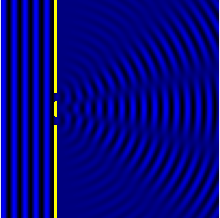

Difraktsioon on füüsikaline nähtus, mille korral laine paindub ümber takistuste või läbib tõkkes oleva väikese ava.[2]. Difraktsioon on eriti märgatav siis, kui tõkke või selles oleva ava mõõtmed on lähedased lainepikkusele. Difraktsiooniline kõrvalekaldumine (paindumine) sirgjoonelisest levimisteest ei tulene peegeldumisest, murdumisest ega hajumisest.[3]
Sarnane nähtus esineb ka siis, kui valguslaine levib läbi aine, millel on levimissihis muutuv murdumisnäitaja, või kui helilaine levib läbi muutliku akustilise impedantsiga keskkonna. Difraktsioon esineb iga liiki lainete puhul, k.a helilainete, veelainete, elektromagnetlainete, nagu näiteks nähtava valguse ja raadiolainete korral. Ka füüsilistel objektidel on lainelised omadused (aatomtasandil), difraktsioon esineb ka mateeria korral ning seda uuritakse kvantmehaanika seaduspärasustega. Itaalia teadlane Francesco Maria Grimaldi võttis kasutusele sõna difraktsioon ja oli esimene, kes tegi 1665. aastal selle nähtuse täpsed vaatlustulemused.[4][5]
Richard Feynman on öelnud, et
- "keegi ei ole kunagi suutnud defineerida interferentsi ja difraktsiooni erinevust rahuldavalt. See on lihtsalt kasutamise küsimus ja nende vahel ei ole mingit kindlat füüsikalist erinevust."[6]
Ta pakkus välja, et kui katses on ainult kaks allikat nagu Youngi kahe pilu katses, kutsuda nähtust interferentsiks, aga suurema arvu allikate korral difraktsiooniks.
Difraktsiooni nähtused on kõige suuremad siis, kui takistuse/ava suurus on umbes samas suurusjärgus laine lainepikkusega. Kui takistavas objektis on mitu lähedal asuvat ava, siis võivad muutuda pärast selle läbimist laine muster ja intensiivsus. See juhtub superpositsiooni tõttu. Tekib interferents, mille korral erinevad laine osad pärast objekti läbimist jõuavad vaatlejani, pärast erineva teepikkuse läbimist (vt difraktsioonivõre).
Difraktsiooni formalismi saab kirjeldada ka nii, et lained levivad piiratud ulatuses vabas ruumis. Kasutades difraktsiooni võrrandeid, saab uurida laserikiire profiili laienemist, radariantenni kiire kuju ja vaatevälja ning ultraheliandurit.
Näited[muuda | muuda lähteteksti]
Difraktsiooninähtuseid on tihti näha ka igapäevaelus. Üks difraktsiooni hästi iseloomustav näide on seotud valgusega; näiteks CD või DVD tihedalt pakitud rajad käituvad kui difraktsioonivõre, mis moodustab tuttava vikerkaaremustri. Seda teadmist kasutades saab välja töötada võre, mille struktuur vastab oodatule; nagu näiteks krediitkaartidel asuvad hologrammid. Difraktsioon atmosfääris tekib väikeste osakeste tõttu, mis saavad tekitada nähtava ereda ringi ümber valgusallika nagu näiteks Päikese või Kuu. Kõik need nähtused on põhjustatud valguse lainelistest omadustest.
Difraktsiooni esineb kõikide lainetüüpide korral. Ookeanilained interfereeruvad ümber kaide ja teiste takistuste. Helilained saavad interfereeruda ümber objektide. Selle tõttu on võimalik kuulda kedagi kutsumas isegi kui ta peidab ennast puu taga.[7] Difraktsioon on probleemiks mitmete tehniliste rakenduste juures; see seab teoreetilise piiri kaamera, teleskoobi või mikroskoobi lahutusvõimele (resolutsioonile).
Ajalugu[muuda | muuda lähteteksti]

Valguse difrakteerumise nähtust uuris ja kirjeldas põhjalikumalt esimeena Francesco Maria Grimaldi, kes ühtlasi lõi ka mõiste difraktsioon ladinakeelsest sõnast diffringere, mis tähendab 'tükkideks purunemist', vihjates sellega valguse murdumisele erinevatesse suundadesse. Grimaldi vaatluse tulemused avaldati postuumselt 1665. aastal.[8][9][10] Isaac Newton uuris neid nähtusi ning omistas need valguskiirte muutumatusele. James Gregory (1638–1675) uuris linnusule tekitatud difraktsioonimustreid. See oli sisuliselt difraktsioonivõre tekitatud nähtuste esmakordne uurimine.[11] Thomas Young korraldas 1803. aastal eksperimendi, kus tutvustas kahest lähedal asetsevast pilust tingitud interferentsi.[12][13] Thomas Young selgitas vaatlustulemusi erinevatest piludest väljuvate lainete interferentsiga ja järeldas, et valgus peab levima lainetena. Augustin-Jean Fresnel tegi põhjalikumaid uuringuid ja arvutusi difraktsiooninähtustest, mis avaldati 1815.[14] ja 1818. aastal.[15] Augustin-Jean Fresnel toetas sellega märkimisväärselt valguslaine teooriat, mida oli uurinud Christiaan Huygens[16] ja taaselustanud Young, vastandades teooriat Newtoni valgusosakeste teooriale.
Mehhanism[muuda | muuda lähteteksti]

Difraktsioon on põhjustatud lainete levimise iseärasustest; seda kirjeldavad Huygensi-Fresneli printsiip ja lainete superpositsiooniprintsiip. Lainete levimist saab visualiseerida, kui arvata iga lainefrondi punkt uueks sfäärilise sekundaarlaine allikaks. Laine levimisteekonna muutus igas järgnevad alampunktis on nende sekundaarlainete summa. Vastavate lainete summa on kindlaks määratud nende suhteliste faaside ja osalainete amplituudidega, nii et summeeritud amplituudi väärtus võib varieeruda nullist kuni osalainete üksikute amplituudide summani. Sellest tulenevalt on tavaliselt difraktsiooni mustritel maksimumi ja miinimumi seeriad.[17]
Difrakteerunud välju on võimalik matemaatiliselt kirjeldada mitmete analüütililiste mudelite abil, sealhulgas Kirchhoffi-Fresneli difraktsioonivõrrandiga, mis on tuletatud lainevõrrandist, Fraunhoferi difraktsiooni lähendiga Kirchhoffi võrrandist, mis kehtib kaugväljadele ning Fresneli difraktsiooni lähendiga, mis kehtib lähiväljadele. Enamikku konfiguratsioone ei ole võimalik analüütiliselt lahendada, kuid lõpliku elemendi meetodi ning piirelemendi meetodi abil on võimalik välja arvutada numbrilisi lahendusi.
Difraktsiooninähtusi on võimalik kvalitatiivselt mõista, võttes arvesse, kuidas individuaalsete sekundaarlainete allikate faasid varieeruvad. Konkreetsemalt öeldes, kuidas muutuvad tingimused, mille korral faasi erinevus on võrdne poole tsükliga. Sel juhul vastavad lained tühistavad teineteist.
Difraktsiooni on lihtsaim kirjeldada juhul, kui nähtust on võimalik kujutada kahemõõtmeliselt. See kehtib näiteks vee lainetuse kohta, kuna veelained levivad vaid veepinnal. Valguse puhul on tihti võimalik eirata üht mõõdet juhul, kui difrakteeruv objekt ulatub mõõtme suunda märkimisväärselt suurema pikkusega, kui lainepikkus. Probleemi kolmemõõtmelist olemust tuleb arvesse võtta, kui valgus paistab läbi väikeste ringikujuliste avauste.
Valguse difraktsioon[muuda | muuda lähteteksti]
Difraktsioon ühe pilu korral[muuda | muuda lähteteksti]

Lõpmata väikese laiusega pilu valgustamisel difrakteerub valgus ringikujuliste lainete jadaks ja lainefront, mis pilust ilmub, on ühtlase intensiivsusega silindriline laine.
Kui valgustatav pilu on laiem, kui temale langeva valguse lainepikkus, siis tekib pilust allavoolu olevas ruumis valguse interferents. Nähtust on võimalik seletada, kui eeldada, et pilul on suur hulk punktallikaid, mis on terve pilu laiuses võrdselt jaotunud. Lihtsustamise mõttes saab käsitleda valgust ühe lainepikkuse jaoks. Kui pilule langev valgus on monokromaatiline, siis on kõigil punktallikatel sama faas. Pilust allavoolu jäävas punktis koosneb valgus iga punktallika panusest ning kui panuste suhtelised faasid erinevad 2π võrra või enam, siis saame leida difrakteerunud valguse miinimumi ja maksimumi. Sellised faasierinevused on tingitud difrakteeruvate valguskiirte vastavasse punkti jõudmiseks läbitud teekonna pikkuste erinevusest.
Nurka, kus difrakteerunud valguse esimene miinimum on saavutatud, on võimalik leida järgneva arutluskäiguga. Pilu ülemise servaga piirnevalt valguse allikalt tulev valgus interfereerub destruktiivselt pilu keskelt tuleva valgusega juhul, kui teekonna erinevus nende vahel on võrdne λ/2. Sarnaselt, valguse allikas, mis asub pilu ülemisest äärest veidi allpool interfereerub destruktiivselt pilu keskmest veidi allpool asuva valgusallikaga. Sama arutluskäik kehtib liikudes piki tervet pilu kõrgust ning sellest järeldub, et terve pilu destruktiivse interferentsi tekketingimused on samad, mis kahe teineteisest poole pilu laiuse kaugusel asuva kitsa pilu vahel tekkiva destruktiivse interferentsi tekke tingimused. Teekonna erinevus väljendub nii et minimaalne intensiivsus ilmneb nurgal θmin, mis on antud kui:
kus
- d on pilu laius,
- valguse langemise nurk, kus ilmneb minimaalne intensiivsus
- on valguse lainepikkus
Kui kujutada, et pilu on jaotatud neljaks, kuueks, kaheksaks osaks jne, siis miinimumid ilmnevad nurkadel θn, antud kui
kus
- n nullist erinev täisarv.
Difraktsioonimustri maksimumi leidmiseks puuduvad lihtsad argumendid. Intensiivsuse profiili saab arvutada kasutades Fraunhoferi difraktsioonivõrrandit:
kus
- on intensiivsus vastava nurga all,
- on langeva valguse intensiivsus, ning
- sinc funktsioon on antud kui sinc(x) = sin(πx)/(πx) kui x ≠ 0, ja sinc(0) = 1
Antud analüüs kehtib ainult kaugväljade puhul, s.t et kaugustel, mis on palju pikemad, kui pilu laius.



Difraktsioonivõre[muuda | muuda lähteteksti]
Difraktsioonivõre on korrapärase mustriga optiline komponent. Läbi võre difrakteerunud valguse kuju sõltub elementide struktuurist ja elementide arvust. Kõigil võredel on intensiivsuse maksimum nurkadel θm, mida väljendab võre võrrand:
kus
- θi on valguse langemise nurk,
- d on võrekonstant
- m positiivne või negatiivne täisarv
Läbi võre difrakteerunud valgus on leitav igalt võreelemendilt difrakteerunud valguse summeerimisega ning see on olemuslikult difraktsioonimustri ja interferentsimustri konvolutsioon.
Apertuur[muuda | muuda lähteteksti]
Punktallikast eralduval lainel on amplituud kohas r, mis on antud punktallika sagedusdomeeni lainevõrrandi lahendist (Helmholtzi võrrand),
Kus on kolmemõõtmeline deltafunktioon. Deltafunktsioonil on vaid radiaalne sõltuvus, mistõttu Laplace'i operaator sfäärilises koordinaatsüsteemis lihtsustub:
Otsese asendusega on võimalik selle võrrandi lahendit leida skalaarse Greeni funktsioonina, mis sfäärilisse koordinaatsüsteemi asetatuna (ning kasutates füüsikalist aja konventsiooni ) on:
Selline lahend eeldab, et deltafunktsiooni allikas asub koordinaatide nullpunktis. Kui deltafunktsiooni allikas asub vabalt valitud punktis, mida tähistatakse vektoriga ning väljapunkt asub punktis , siis võib kujutada skalaarset Greeni funktsiooni (vabalt valitud allika asukoha jaoks) kui:
Järelikult, kui elektriväli Einc(x,y) langeb avale, siis ava distributsioonist tekitatud väli väljendub pindintegraalina:

kus avas olevat punktallikat iseloomustab vektor:
Kaugväljas, kus saab rakendada paralleelsete kiirte lähendit, on Greeni funktsioon esitatav kujul:
Lihtsustub kui:
Fraunhoferi regiooni välja avaldis muutub:
Kuna
ning
Siis Fraunhoferi regiooni välja avaldis tasandilisest avast muutub:
Lastes:
ning
Siis Fraunhoferi regiooni väli tasandilisest avast saab Fourier' teisendus kuju:
Fraunhoferi regioonis saab avaldisest ava distributsiooni ruumiline Fourier' teisendus. Aval rakendatav Huygensi printsiip väidab, et kaugvälja difraktsioonimuster on ava kujuga ruumiline Fourier' teisendus ning et see on paralleelsete kiirte lähenduse otsene kõrvalsaadus. See omakorda on identne ava tasandilistele väljadele tasandilise laine dekompositsiooni rakendamisega.
Laserikiire levimine[muuda | muuda lähteteksti]
Laserikiire Gaussi profiili muutumise kiire levimise ajal määrab difraktsioon. Laseri väljundpeegel on ava ning järgneva kiire kuju määrab see ava. Järelikult, mida väiksem on väljundkiir, seda kiiremini ta hajub.
Paradoksaalselt on võimalik vähendada laserikiire hajuvust esmalt seda kumerläätse abil laiendades ning seejärel teise kumerläätse, mille fookus langeb kokku esimese kumerläätse fookusega, abil kiirt kalibreerides. Tulemuseks saadaval kiirel on suurem ava ja seetõttu ka väiksem hajuvus.
Difraktsiooni käitumismustrid[muuda | muuda lähteteksti]
Difraktsiooni üldiselt iseloomustavad omadused:
- Mida väiksem on difrakteeruv objekt, seda "laiem" on tulenev difraktsioonimuster ja vastupidi. (Täpsemalt öeldes kehtib see nurga siinustele.)
- Difraktsiooni nurgad on skaleerimise korral muutumatud – need sõltuvad vaid lainepikkuse ja difrakteeruva objekti suhtest.
- Kui difrakteeruval objektil on perioodiline struktuur, näiteks difraktsioonivõre puhul, muutuvad objekti omadused olulisemaks.
Viited[muuda | muuda lähteteksti]
- ↑ Dietrich Zawischa. "Optical effects on spider webs". Vaadatud 21.09.2007.
- ↑ HyperPhysics "Difraktsioon"
- ↑ ENE 2. köide, 1987
- ↑ Francesco Maria Grimaldi, Physico mathesis de lumine, coloribus, et iride, aliisque annexis libri duo (Bologna ("Bonomia"), Italy: Vittorio Bonati, 1665), page 2:
Original : Nobis alius quartus modus illuxit, quem nunc proponimus, vocamusque; diffractionem, quia advertimus lumen aliquando diffringi, hoc est partes eius multiplici dissectione separatas per idem tamen medium in diversa ulterius procedere, eo modo, quem mox declarabimus.
Tõlge : See on meid valgustanud ja andnud teise, neljanda tee, mille me nüüd teeme teatavaks ja nimetame "difraktsiooniks" [st osadeks jagunemiseks], sest mõnikord me jälgime valguse lahknemist; see tähendab, et osad ühendist [st valguskiired], eraldatud jagunemise teel, liiguvad edasi läbi aine, kuid erinevates suundades, nagu me varsti näitame.
- ↑ Cajori, Florian "A History of Physics in its Elementary Branches, including the evolution of physical laboratories." MacMillan Company, New York 1899
- ↑ R. Feynman, Lectures in Physics, Vol, 1, 1963, pg. 30-1, Addison Wesley Publishing Company Reading, Mass
- ↑ Andrew Norton (2000). Dynamic fields and waves of physics. CRC Press. Lk 102. ISBN 978-0-7503-0719-2.
- ↑ Francesco Maria Grimaldi, Physico-mathesis de lumine, coloribus, et iride, aliisque adnexis... [Valguse, värvi, vikerkaare jne füüsikaline matemaatika] (Bologna ("Bonomia"), Italy: Vittorio Bonati, 1665), pp. 1–11: "Propositio I. Lumen propagatur seu diffunditur non solum directe, refracte, ac reflexe, sed etiam alio quodam quarto modo, diffracte." (Ettepanek 1. Valgus levib mitte ainult sirgjooneliselt, murdumise ja peegeldumise kaudu, aga ka mõnevõrra erineval neljandal viisil: difraktsiooniga)
- ↑ Jean Louis Aubert (1760). Memoires pour l'histoire des sciences et des beaux arts. Paris: Impr. de S. A. S.; Chez E. Ganeau. Lk 149.
- ↑ Sir David Brewster (1831). A Treatise on Optics. London: Longman, Rees, Orme, Brown & Green and John Taylor. Lk 95.
- ↑ Letter from James Gregory to John Collins, dated 13 May 1673. Kordustrükk: Correspondence of Scientific Men of the Seventeenth Century...., ed. Stephen Jordan Rigaud (Oxford, England: Oxford University Press, 1841), vol. 2, pp. 251–255, eriti p. 254.
- ↑ Young, Thomas (01.01.1804). "The Bakerian Lecture: Experiments and calculations relative to physical optics". Philosophical Transactions of the Royal Society of London. Royal Society of London. 94: 1–16. DOI:10.1098/rstl.1804.0001.. (Märge: See loeng esitati Kuninglikule Ühingule 24. novembril 1803. aastal)
- ↑ Jaak Jaaniste loengumaterjalid: "Thomas Youngi katse"
- ↑ Augustin-Jean Fresnel (1816) "Mémoire sur la diffraction de la lumière … ," Annales de la Chemie et de Physique, 2nd series, vol. 1, pages 239–281. (Esitletud l'Académie des sciences 15. oktoobril 1815. aastal) Internetis kättesaadav: Bibnum.education.fr
- ↑ Augustin-Jean Fresnel (1826) "Mémoire sur la diffraction de la lumière," Mémoires de l'Académie des Sciences (Paris), vol. 5, pages 33–475. (Esitatud l'Académie des sciences Pariisis 20. aprillil 1818. aastal.)
- ↑ Christiaan Huygens, Traité de la lumiere... (Leiden, Netherlands: Pieter van der Aa, 1690), Chapter 1. From p. 15: "J'ay donc monstré de quelle façon l'on peut concevoir que la lumiere s'etend successivement par des ondes spheriques,..." (Ma olen nii näidanud nagu võibki ettekujutada, et valgus levib edukalt sfääriliste lainetena,...)(Märge: Huygens avaldas oma Traité 1690. aastal; kuigi raamatu eessõnas, Huygens märgib ära, et esimest korda esitles ta oma raamatut 1678. aastal Prantsuse Kuninglikule Teaduste Akadeemiale.)
- ↑ Jaak Jaaniste loengumaterjalid: "Huygensi-Fresnelli printsiip"



























