Laurent'i rida

Laurent'i rida defineeritakse teatud punkti c ja teatud integreerimisraja γ suhtes. Integreerimisraja peab asuma rõnga (tähistatud punasega) sees, kus f(z) on analüütiline.

Laurent'i rida on kompleksmuutuja funktsiooni esitus astmereana, mis sisaldab ka negatiivseid astendajaid. See on oma nime saanud prantsuse matemaatiku Pierre Alphonse Laurent'i järgi, kes selle aastal 1843 esmakordselt avaldas.

Definitsioon

Kompleksmuutuja funktsiooni f(z) Laurent'i rida punkti c suhtes on:

$f(z)=\sum_{n=-\infty}^\infty a_n(z-c)^n \, ,$

kus kordajad a_n on antud joonintegraalina:

$a_n=\frac{1}{2\pi i} \oint_\gamma \frac{f(z)\,\mathrm{d}z}{(z-c)^{n+1}}.\,$

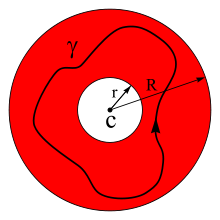
Viimane avaldis on Cauchy integraalvalemi üldistus. Integaali raja γ on vastupäeva suunatud pidev suletud joon, mis ümbritseb punkti c ja paikneb rõngal, kus f(z) on regulaarne. f(z) rittaarendus kehtib kõikjal rõnga sisemus.

Vaata ka

• Cauchy integraalvalem
• Taylori rida
• Fourier rida