Lainik

Lainik on lõplik laine tüüpi võnkumine, mida saab kirjeldada lühikese ostsillatsioonina ehk võnkumisena. Lainikuid kasutatakse signaalide analüüsimiseks just eriti signaalitöötluses ja ka mitmes matemaatikaharus. Põhiliselt uuritakse lainikute abil signaale, mis on katkendlikud, lõplikud ning mis sisaldavad järske hüppeid ja kiireid muutusi ajas. Lainiku kasutamise mõte on selles, et me saame analüüsida signaali vastavalt tema skaalale ja ehitusele. Lainikute abil on võimalik saada infot kogu signaali kohta, sealhulgas ka väga väikeste ja täpsete osade kohta.

Sarnaselt on võimalik kasutada Fourier' teisendusi, et signaali uurida, kuid erinevus tuleb just sellest, et Fourier' teisendusteks kasutatakse siinus- ja koosinuslaineid, et esitada algsignaali. Probleem seisneb selles, et Fourier' teisendus on oma olemuselt mittelokaalne ehk lõpmatu ulatusega (-∞, ∞). Ehk kui me uurime signaalis lühiajalisi drastilisi muutusi, siis ei saa me Fourier' teisendusega eriti täpset tulemust. Samuti ei saa Fourier' teisenduse abil signaali sageduskomponente ajas lokaliseerida, kuid lainikute abil on see võimalik. Sellepärast kasutataksegi lainikuid ja nende abil tehtavaid matemaatilisi teisendusi, mida omakorda nimetatakse lainikute teisenduseks (wavelet-transform).

Ajalugu

Haari lainik

Lainikud ja lainikute teisendused said alguse juba 1909. aastal. Esimese lainiku autoriks nimetatakse Alfréd Haari, kelle järgi on nimetatud Haari lainik. Olemuselt on Haari lainik ruudukujuliste signaalide järgnevus, mis moodustab lainiku. Kuigi esimeseks lainikuks nimetatakse Haari lainikut, siis nimetused "lainik" ja "lainikute uurimine" tulid alles aastaid hiljem. Haari lainik on ka olemuselt kõige lihtsam. Selle abil on lihtsasti võimalik esitada väga kiireid muutusi signaalis, kuid sellega selle lainiku otstarve piirdubki. See tuleneb sellest, et Haari lainik ei ole pidev..

Mõisted "lainik" ja "lainiku teisendus" said alguse prantsuse geofüüsikust Jean Morlet'st, kes kasutas lainikud, et analüüsida Maa seismilisi signaale, mis kandsid geoloogiliste kihtide infot. Morlet alustas analüüsi akendatud Fourier' teisendustega, kuid järeldas kiiresti, et tekkivate artefaktide hulk on liiga suur ning on vaja võtta kasutusele midagi täpsemat.

Lainikutüübid

Lainikuks nimetatakse funktsiooni Ψ(t), mille kohta kehtib kindel tingimus, et lainiku energia on lõplik. Valemina väljendub see järgmiselt.

$\int _{-\infty }^{\infty }{|\psi {\left(t\right)|}^{2}dt<}\infty$

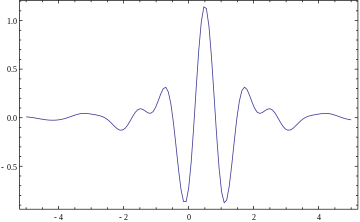
Lõpliku energia all mõistetakse seda, et lainikul on reaalteljel nii algne kui ka lõplik reaalarvuline väärtus. Sellise definitsiooniga lainikuid nimetatakse sageli ka emalainikuteks. Emalainikuid on mitut tüüpi.

Meyeri lainik

Morlet' lainik

Sombreerolainik (Mexican hat)

Lainikute teisendused

Põhiline lainikute teisenduse idee seisneb selles, et tulemus pärast teisendust mõjutaks ainult aja kestvust, mitte kuju. Selle jaoks konstrueeritakse spetsiaalsete parameetritega funktsioonid, mis toetuvad ka signaalitöötluse määramatuse printsiibile

$\Delta t\Delta \omega \geqq {\frac {1}{2}}$ ,

kus t näitab aega ja ω nurksagedust. Selle järgi saame teha järelduse: kui Δt on suur, siis ajadomeeni täpsus väheneb ja sagedusdomeeni täpsus suureneb. Ning vastupidi: kui Δt on väike, siis ajadomeenis saame täpsemad tulemused ja sagedusdomeenis vähem täpsed tulemused.

Pideva lainiku teisendus

Kui meil on lainikufunktsioon Ψ ja mingi suvaline signaal x(t), siis saame pideva lainiku teisenduse valemi esitada järgmiselt:

$X_{w}(a,b)={\frac {1}{|a|^{1/2}}}\int _{-\infty }^{\infty }x(t){\overline {\psi }}\left({\frac {t-b}{a}}\right)\,dt$ ,

kus Ψ(t) on pidev funktsioon nii aja kui ka sageduse järgi ning mida sageli nimetatakse ka emalainikuks. Parameeter a näitab lainiku skaleeritust ja b nihet ajas. :

Lainikute kasutusala

Põhiliselt kasutatakse lainikuid signaalitöötluses ja teatud matemaatika valdkondades.

Signaalitöötluses kasutatakse lainikuid enamasti selleks, et algsignaali mingil viisil töödelda. Näiteks saab kasutada lainikute omadusi, et algset signaali info poolest niimoodi vähendada, et signaali kuju ei lähe ei ajadomeenis ega sagedusdomeenis kaduma. Selleks tuvastatakse signaali kõige vähem mõjutatavad osad ning eemaldatakse need.

Samuti on võimalik lainikute abil tuvastada piltide ääri, kuna lainikud on väga hästi kasutatavad kohtades, kus toimuvad kiired muutused (pildi ääred).

Matemaatikas on võimalik lainikute abil teha väga kiireid arvanalüüse, näiteks lahendada diferentsiaalvõrrandeid.