Kummituskuva
Kummituskuva on optikas kasutatav kuvamismeetod, millega saadakse objekti detailne kujutis, kuigi objektilt tulevat valgust mõõdab ilma ruumilise lahutusvõimeta kaamera või integreeriv intensiivsuse andur.
Hoolimata intrigeerivast nimest on kummituskuva siiski täiesti füüsikaline nähtus. Nimetus tuleneb esimestes eksperimentides saadud kujutiste kummituslikust hägususest.
Teoreetilised alused[muuda | muuda lähteteksti]
Kummituskuva tekitamiseks saab kasutada mõõdetavate intensiivsuste fluktuatsioonide korrelatsiooni:
,
kus ja on vastavalt intensiivsuse hetkväärtus ja keskväärtus. Punkti kohavektor on ja vaadeldav sagedus on . Tihti juhtub, et fluktuatsioonid alluvad Gaussi statistikale, mispuhul avaldub intensiivsuse fluktuatsioonide vaheline korrelatsioon järgmiselt:
Siinkohas tähistavad nurksulud üle footonite ansambli keskmistamist. Suurust
nimetatakse spektraalseks ristkorrelatsiooniks. ja on väljad objektiõlas ja võrdlusõlas detektorite asukohal. Nüüd saab sõltuvalt levikuseaduste valikust leida spektraalse tihedusfunktsiooni ja siduda mõõdetava korrelatsiooni enda uuritava objekti läbilaskvuse (mis võib ka olla kompleksne) ja süsteemi geomeetriliste parameetritega, et leida süsteemi läbilaskvus. Sellist meetodit on kasutatud edukalt faasiobjektide kuvaks.[1]
Ajalugu[muuda | muuda lähteteksti]
Kummituskuva on uudne ja huvitav kuvamismeetod, kuid sellest hoolimata keerulise ja mitmeetapilise arengukäiguga. Vähem kui kahekümne aastaga on näidatud, et selline objektide kuvamine on teostatav, kusjuures nii üksikuid footoneid kui ka klassikalist valgust kasutades. Klassikaliste valgusallikate valgus on laia ja pideva spektriga ning mittekoherentne. On näidatud, et nende meetodite suurim erinevus on signaali ja müra võimsuse suhe. Nimelt saadakse kvantefekti ära kasutades tunduvalt puhtam signaal.[2]
Esimene eksperiment – kummituskuva paardunud footonitega[muuda | muuda lähteteksti]
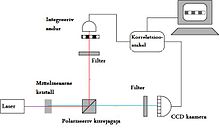
Kummituskuva võimalikkust tõestav esimene eksperiment korraldati 1995. aastal. Selles kasutati kvantseostatud footoneid ehk põimfootoneid. Viimased tekitati mittelineaarse optilise efekti abil, mida nimetatakse spontaanseks parameetriliseks allamuundumiseks. Selle käigus ergastatakse pumpava laseriga vastava mittelineaarse efekti tekkeks sobivat kristalli (selle eksperimendi puhul oli tegu beeta-baariumboraadiga ). Kuna kehtima jäävad nii impulsi kui ka energia jäävuse seadused, siis tekivad madalama sagedusega footonite paarid, mis on omavahel kvantmehaaniliselt seostatud niinimetatud õudse vastastikmõju kaudu.[3]
Tekkinud seostatud footonite kimbud jagati kaheks kiireks polariseeriva kiirejagajaga. Üks neist kahest kiirest – nimetagem seda mõõteõlaks – juhiti uuritavale objektile, milleks viidatud eksperimendis oli aukudega plaat (laineoptilises käsitluses võib seda nimetada kahendamplituudi maskiks, kuna objekt muudab vaid teda läbiva signaali amplituudi funktsioonina koordinaadist, jättes valguse faasi muutumatuks) ja seejärel koguti valgus kokku ühestainsast pikslist koosnevasse intensiivsuse andurisse. Teist kiirt – nimetagem seda võrdlusõlaks – mõõdeti sarnase anduriga, kuid seda tehti skaneerivalt – anduri asukohta kiire risttasandis muudeti. Sellega saavutati ruumiline resolutsioon, kuid objektiinfot siiski ei mõõdetud. Kirjeldatud meetodi asemel saab kasutada lihtsalt sobivat mitmepikslilist andurit, näiteks CCD-kaamerat. Seejärel võrreldi kahe anduri signaale. Kujutis konstrueeriti, teades, et kui signaalianduris pole signaali, siis samal hetkel püütud võrdlusõla footonite paarisfootonid tabasid objekti, ning kui signaaliõlas registreeriti footon, siis läbis ta objekti mõnda auku ja seega saab samal ajal võrdlusõlast püütud footoni järgi teada selle augu asukoha objektis.[3]
Erinevad meetodid amplituudikuvaks[muuda | muuda lähteteksti]
Lisaks eelnevalt kirjeldatud eksperimendile, kus kummituskuva jälgimiseks kasutati valguse kvantomadusi, saab mitmesuguseid amplituudiobjekte kuvada ka klassikalise valgusega. Sellisel juhul jälgitakse üksikute rangelt korreleeritud footonpaaride asemel hoopis suuri footonite gruppe.
Kummituskuva koherentse valgusallikaga[muuda | muuda lähteteksti]

2002. aastal näidati, et kvantpaardunud footonite olemasolu pole kummituskuva tekitamiseks tarvilik: kasutada võib ka klassikalist valgust, näiteks laserikiirgust. Laserikiirguse eripäraks on teadupärast see, et valguse koherentsi teepikkus on võrreldes soojuslike allikatega väga suur, samuti on laserite ruumiline ja ajaline koherentsus võrreldes klassikaliste valgusallikatega väga suur. Viidatud eksperimendis kasutati väga kitsa kiirega laserit. Selle kiires liiguvad kõik footonid heas lähenduses ühes suunas – footonid on korreleeritud suuna suhtes. Nüüd suunati see kiir kiirelt ja juhuslikult kaldenurki muutvale peeglile (peegel värises), misjärel jagati kimp kiirejagajaga kaheks ja saadeti kahte õlga nagu eelnevas eksperimendis. Kujutist konstrueerides leiti, et kujutise kvaliteet oli oluliselt halvem kui paardunud footonitega eksperimendis. Selle põhjuseks on asjaolu, et footonite suunaline korrelatsioon polnud täielik.[4]
Kummituskuva soojusliku valgusega[muuda | muuda lähteteksti]
2004. aastal näidati, et kummituskuva saab tekitada ka soojuskiirgusliku valgusega. Sellise valguse spektraalne intensiivsusjaotus allub musta keha kiirguse jaotusele. [5]
Ühe anduriga kummituskuva[muuda | muuda lähteteksti]

Olgu nüüd valgusallikaks soojuslikku müra tekitav klassikaline valgusallikas. Kummituskuva nägemiseks on vaja võrrelda objektile langevat valgust ja objektilt mõõdetud integraalset signaali. See tähendab, et tingimata pole vaja mõlemat signaali mõõta, piisab vaid sellest, kui teame objektile langenud valguse intensiivsusjaotust kogu objektitasandil ja suudame seda varieerida. Sellise tähelepaneku tegid 2009. aastal Iisraeli füüsikud. Valgusvälja varieerimiseks kasutati ruumilist valgusvälja modulaatorit (edaspidi SLM (Spatial Light Modulator)), mis tõhusalt töötas amplituudimaskina – SLM pinna erinevate punktide peegelduskoefitsienti saab lihtsalt arvutikontrolliga mõõta.[6]
Faasikuva[muuda | muuda lähteteksti]
Erinevalt eelmistest juhtudest, kus kummituskuvaga on kuvatud amplituudiobjekte, saab mittekoherentse valgusega kuvada ka faasiobjekte. Eespool teooria osas on toodud selle teoreetilise motivatsiooni arutluskäik.[7]
Kummituskuva potentsiaalsed rakendused[muuda | muuda lähteteksti]
Kummituskuva võimalikeks rakendusteks peetakse võimalust kuvada läbi raskesti läbinähtavate keskkondade, näiteks turbulentse atmosfääri[8]. Samuti on näidatud, et andmetöötlusmeetodit compressed sensing kasutades saab kummituskuvades vähendada kujutise saamiseks vajalike mõõtepunktide arvu. See tähendab, et N-pikslise resolutsiooni saab mõõteriistaga, millel on vähem kui N pikslit. See meetod võib leida rakendusi mikroskoopias ja LIDAR-tehnikas.[9]
Viited[muuda | muuda lähteteksti]
- ↑ Shirai, Setäla, Friberg, “Ghost imaging of phase object with classical incoherent light,” Phys. Rev. A 84 (2011), 041801
- ↑ Erkmen, Shapiro, “Ghost Imaging”. Adv. Opt. Photon. 2, 405–450, (2010)
- ↑ 3,0 3,1 Pittman, Shih, Strekalov, Sergienko, “Optical imaging by means of two-photon quantum entanglement,” Phys. Rev. A 52 (1995), R3429
- ↑ Bennink, Bentley, Boyd, “‘Two-photon’ coincidence imaging with a classical source,” Phys. Rev. Lett. 89 (2002), 113601
- ↑ A. Gatti, E. Brambilla, M. Bache, and L. A. Lugiato, Phys. Rev. Lett. 93 (2004), 093602
- ↑ Bromberg, Katz, Silberberg, “Ghost imaging with a single detector,” Phys. Rev. A 79 (2009), 053840
- ↑ Shirai, Setäla, Friberg, “Ghost imaging of phase object with classical incoherent light”, Phys. Rev. A 84 (2011), 041801
- ↑ Cheng, “Ghost imaging through turbulent atmosphere,” Optics Express, Vol. 17, Issue 10 (2009), lk 7916–7921
- ↑ 'Compressive Ghost Imaging' by O. Katz, Y. Bromberg and Y. Silberberg










