Koherentsed lained
Koherentseteks laineteks nimetatakse füüsikas laineid, millel on konstantne faasivahe ja püsiv sagedus. See annab lainetele ideaalse omaduse, mis võimaldab statsionaarses olekus interferentsi. Koherentsete lainete kohtumisel tekib interferents, kus lained tugevdavad või nõrgendavad üksteist.[1] Koherentsus sisaldab mitmeid erinevaid kontseptsioone piirjuhtudele, mis tegelikult reaalsuses ei esine. Samas võimaldavad need paremini mõista lainete füüsikalisi omadusi, mistõttu interferents on ka üks kõige olulisemaid põhimõisteid kvantmehaanikas. Üleüldiselt väljendab koherentsus korrelatsioone lainete või mitme lainepaketi füüsikaliste suuruste vahel.
Matemaatilises mõistes ei ole interferents midagi enamat kui juurde lisatud lainete funktsioonid. Kvantmehaanikas võib üksik laine iseendaga seguneda, see tuleneb tema kvantomadusest, kus laine võib sellegipoolest jaotuda kaheks (vaata Youngi kahepilu katset). See tähendab, et konstruktiivne või destruktiivne interferents on piirjuhud, ning seetõttu võivad nende lained alati üksteist liita, isegi siis kui tulemus võib olla keeruline või ei ole märkimisväärne.
Kahe laine segamisel võivad need omavahel luua laine, mille amplituud on suurem kui nende kummagi algsed amplituudid, lained tugevdavad üksteist (konstruktiivne interferents). Võib toimuda ka lainete nõrgenemine, kus uue laine amplituud on algsetest palju väiksem (destruktiivne interferents). Konstruktiivne ja destruktiivne interferents sõltuvad faasivahest. Kaks lainet on koherentsed, kui neil on konstantne suhteline faas. Koherentsuse astet[2] mõõdetakse interferentsipildi nähtavusega, mis näitab, kui hästi lained üksteist kustutavad destruktiivse interferentsiga.
Ruumiline koherentsus kirjeldab korrelatsiooni lainete vahel, mis asuvad ruumi eri punktides. Ajaline koherentsus kirjeldab korrelatsiooni või ennustavat suhet lainete vahel, mis on vaadeldud erinevatel ajamomentidel. Mõlemad on jälgitavad nii Michelsoni-Morley katses[3] kui ka Youngi interferentsi katses[4]. Kui Michelsoni-Morley katsest on äärised leitud ning kui ühte peeglit liigutakse aeglaselt eemale, siis laine peab läbima pikema aja ning seetõttu muutuvad ääred rohkem tuhmimaks kuni kaovad täienisti, näidates ajalist koherentsust. Sarnaselt Youngi kahe pilu katsega, kus kahe pilu kauguse suurendamisel koherents väheneb, kuni kõik ääred kaovad, näidates ruumilist koherentsust.
Koherentsus pärineb algselt Thomas Youngi kahe pilu katsest, kuid nüüd kasutatakse seda laialdaselt näiteks akustikas, elektrotehnikas, neuroteaduses ja kvantmehaanikas. Koherentsed omadused on aluseks ka sellistele kaubanduslikele rakendustele nagu holograafia, Sagnaci güroskoop, liitantennid, optiline koherentne tomograaf ja raadioteleskoop.
Koherentsus ja korrelatsioon[muuda | muuda lähteteksti]
Koherentsus kahe lainena tuleneb sellest, kui hästi on korrelatsioonis lained kvantitatiivselt ristkorrelatsiooni[5][6][7][8][9] funktsioonis. Ristkorrelatsioon võimaldab meil ennustada teise laine väärtust juhul, kui me teame esimese laine väärtust. Näiteks kui kaks lainet on kogu aeg pidevas korrelatsioonis, siis muutes esimest lainet, muutuvad samamoodi ka teise laine omadused. Kui mõlemaid laineid kombineerides näitavad need kogu aeg täielikku konstruktiivset interferentsi, järeldub sellest, et nad on täiuslikult koherentsed. Nagu on allpool selgitatud, ei pea teisel lainel olema eraldi olemus. See võib olla esimene laine erineval ajahetkel või teises asukohas. Sel juhul on korrelatsiooni väärtus enesekorrelatsiooni funktsioon. Korrelatsiooni tase sisaldab korrelatsiooni funktsioone.
Lainesarnaste olekute näiteid[muuda | muuda lähteteksti]
Järgnevalt toodud olekuid on võimalik kirjeldada lainevõrrandina või sarnaste lähendustega:
- Lained, mis tekivad nööri liigutamisel (vedruga) üles ja alla
- Vee pinnalained
- Elektrisignaalid ülekandeliinidel
- Heli
- Valguslained
- Elektronid, aatomid
Nendes süsteemides saab lainet mõõta otsese mõõtmisega. Järelikult võib tema korrelatsiooni teiste lainetega lihtsasti välja arvutada. Kuid optikas ei saa mõõta elektrivälja otsese mõõtmise teel, kuna elektriväli võngub palju kiiremini kui detektori ajaline resolutsioon. Selle asemel on võimalik mõõta valguse intensiivsust. Enamus koherentsusega seotud käsitlusi, mida allpool tutvustatakse, loodi optika alal ning hiljem hakati neid kasutama teistes valdkondades. Seetõttu on paljud koherentsuse standardmõõtudest kaudsed mõõdud, isegi valdkondades, kus lainet on võimalik mõõta otsese mõõtmise teel.
Ajaline koherentsus[muuda | muuda lähteteksti]

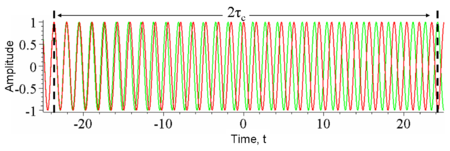
Ajaline koherentsus on keskmistatud korrelatsioon laine väärtusega ja lainega, mis on jäänud maha aja τ võrra. Ajaline koherentsus näitab, kui monokromaatiline on allikas. Teiste sõnadega, see näitab kui hästi võib laine end mõnel teisel ajahetkel segada. Viivitust, mille jooksul faas ja amplituud muutuvad märkimisväärselt, nimetatakse koherentseks ajaks[5] τc. Kui τ = 0, siis koherentsuse tase on ideaalne, samas langeb see märkimisväärselt hilinemisega τc. Koherentsuse teepikkus[5] Lc on määratud kui kaugus, mille jooksul laine läbib aja τc sees. Siin peab jälgima, et ei aetaks segamini koherentsuse aega ajaga, mille jooksul signaal kestab, ega ka koherentsuse teepikkust koherentsuse alaga.
Koherentsuse aja ja signaali kestvuse ajaline suhe[muuda | muuda lähteteksti]
Võib näidata, et mida kiiremini laine korreleerub (ja seda väiksem on τc), seda suurem on laine Δf sageduste ulatus. Seetõttu võib kirjutada:
- .
Formaalselt tuleneb see konvolutsiooni teoreemist[10], mis on seotud Fourier' teisendustega[11] võimsuse spektris (intensiivsus igal sagedusel) tema autokorrelatsioonile[12].
Ajalise koherentsuse näiteid[muuda | muuda lähteteksti]
- Laine, mis sisaldab ainult ühte kindlat sagedust (monokromaatiline), on kogu aja jooksul ideaalselt korreleeritud (näide 1).
- Seevastu laine, mille faas muutub kiiresti, omab väikest koherentsuse aega (näide 2).
Monokromaatilised allikad on tavaliselt laserid; kõrge monokromaatilisus tähendab pikka koherentsuse teepikkust (võib ulatuda sadade meetriteni). Näiteks tasakaalustatud ja monotoonne heelium-neoonlaser võib toota valgust, mille koherentsuse teepikkuse kaugus ulatub 300 meetrini.[13]
Ruumiline koherentsus[muuda | muuda lähteteksti]
Teatud süsteemides, näiteks veelainetes või optikas, võivad lainesarnased olekud ulatuda üle ühe või kahe dimensiooni. Ruumiline koherentsus kirjeldab kahe punkti (x1 ja x2) võimet laine ulatuses teineteist segada, kui need on ajaliselt keskmistatud. Veel täpsemalt, ruumiline koherentsus on ristkorrelatsioon ükskõik mis ajahetkel laines olevate kahe punkti vahel. Kui lainel on ainult üks amplituudi väärtus üle lõpmata pika aja, siis on ta täiuslikult ruumiga koherentne. Eraldatuse vahemik kahe punkti vahel, kus esineb märkimisväärne häirimine, nimetatakse koherentsuse alaks, Ac. See on olulist tüüpi koherentsus, kuna esineb Youngi kahe pilu interferomeetrias. Seda kasutatakse ka optilistes pilditehnika süsteemides, eelkõige erinevates astronoomilistes teleskoopides.
Spektraalne koherentsus[muuda | muuda lähteteksti]


Eri sagedusega lained (valguse puhul esinevad need eri värvidena) saavad üksteist häirida (näide 3), juhul kui neil on fikseeritud suhteline faasi-suhe (vaata Fourier' teisendust). Vastupidi, kui lained erinevatel sagedustel ei ole koherentsed, siis neid liites (kombineerides) tekib laine, mis on ajas pidev, näiteks valge müra (näide 4). Impulsi ajaline kestus on piiratud valguse spektraalse ribalaiusega järgmiselt:
- ,
millest tuleneb Fourie teisenduse omapära – Küpfmülleri määramatuse printsiip (kvantosakestele tuleneb siit Heisenbergi määramatuse printsiip[14]). Kui faas sõltub lineaarselt sagedusest (), siis impulss omab oma ribalaiuse jaoks minimaalset ajalist kestvust, vastasel juhul on see täkkeline (vaata dispersiooni)
Rakendused[muuda | muuda lähteteksti]
- Koherentsed superpositsioonid optilistes laineteväljades sisaldavad holograafiat. Holograafilisi objekte kasutatakse tihti argielus, näiteks rahatähtedel ja krediitkaartidel.
- Sagnaci efekti põhiselt töötav güroskoop.
- Raadioteleskoobid.
- Liitantennid.
Vaata ka[muuda | muuda lähteteksti]
Viited[muuda | muuda lähteteksti]
- ↑ Walter Scheider. "Do the "Double Slit" Experiment the Way it Was Originally Done" (inglise). Vaadatud 19. mai 2013.
- ↑ Eugene Hecht (2002). Optics. 4th ed, 393–396
- ↑ Michelson, Albert Abraham & Morley, Edward Williams (1887). . American Journal of Science. 34: 333–345.
{{cite journal}}: CS1 hooldus: mitu nime: autorite loend (link) - ↑ "Young's Double Slit Experiment" (inglise). Vaadatud 19. mai 2013.
- ↑ 5,0 5,1 5,2 Rolf G. Winter; Aephraim M. Steinberg (2008). "Coherence". AccessScience. McGraw-Hill.
- ↑ Eugene Hecht (2001). Optics (4th ed.). Addison-Wesley. ISBN 978-0805385663.
- ↑ Loudon, Rodney (2000). The Quantum Theory of Light. Oxford University Press. ISBN 0-19-850177-3.
- ↑ Leonard Mandel; Emil Wolf (1995). Optical Coherence and Quantum Optics. Cambridge University Press. ISBN 0-521-41711-2.
- ↑ Frank L Pedrotti; Leno M Pedrotti; Leno S Pedrott (2006). Introduction to Optics. Addison-Wesley. ISBN 978-0131499331.
- ↑ Crutchfield, Steve (9. oktoober 2010), "The Joy of Convolution", Johns Hopkins University, vaadatud 19. november 2010
- ↑ Bracewell, R. N. (2000), The Fourier Transform and Its Applications (3rd ed.), Boston: McGraw-Hill, ISBN 0-07-116043-4
- ↑ Dunn, Patrick F. (2005). Measurement and Data Analysis for Engineering and Science. New York: McGraw–Hill. ISBN 0-07-282538-3.
- ↑ Saleh, Teich. Fundamentals of Photonics. Wiley.
- ↑ Griffiths, David (2005), Quantum Mechanics, New Jersey: Pearson





