Määratud integraal

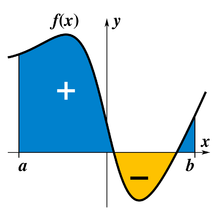
Olgu reaalmuutuja funktsioon $f(x)$ pidev ja tõkestatud lõigus [a, b], siis määratud integraal

\int _{a}^{b}f(x)\,dx\,

on arvuliselt võrdne xy-tasandil funktsiooni $\ f(x)$ graafiku, x-telje ning vertikaalsete sirgetega x = a ja x = b piiratud kujundi märgiga pindalaga, s.o x-teljest ülespoole ja allapoole jääva osa pindalade vahega.

Newtoni-Leibnizi valem

Pikemalt artiklis Newtoni-Leibnizi valem

Olgu funktsioon $\ f(x)$ lõigus [a, b] integreeruv ja leidugu tal selles lõigus algfunktsioon $\ F(x)$ . Siis

\int _{a}^{b}f(x)\,dx=F(x){\Big |}_{a}^{b}=F(b)-F(a)\,

Arve a ja b nimetatakse vastavalt integraali alumiseks ja ülemiseks rajaks. Lõiku [a; b] nimetatakse integreerimislõiguks.

Näide

\int _{0}^{2}2x\,dx=x^{2}{\Big |}_{0}^{2}=2^{2}-0^{2}=4\,

Riemanni integraalsumma

Olgu a ja b reaalarvud (a < b), siis lõigu [a,b] saab jaotada osalõikudeks nii, et

a=x_{0}\leq t_{1}\leq x_{1}\leq t_{2}\leq x_{2}\leq \cdots \leq x_{n-1}\leq t_{n}\leq x_{n}=b.\,\!

Lõigu [a,b] n osalõiguks [x_i−1, x_i] jaotamisel (i=1,2,...,n) ja fikseerides igas osalõigus suvaliselt mingi punkt t_i ∈ [x_i−1, x_i], avaldub funktsiooni f(x) Riemanni integraalsumma lõigus [a, b] kujul

\sigma =\sum _{i=1}^{n}f(t_{i})\Delta _{i}=\sum _{i=1}^{n}f(t_{i})(x_{i}-x_{i-1}),

kus iga liige summas on väikese ristküliku pindala. Ristküliku kõrgus on võrdne funktsiooni väärtusega kohal t_i ja laius on sama mis osalõigu [x_i−1, x_i] pikkus Δ_i. Olgu Δ_i = x_i−x_i−1 osalõigu i pikkus; siis osalõikude maksimaalne pikkus on λ=max_1≤i≤n Δ_i. Seega esindab λ kõiki selliseid jaotusi, sõltumata jaotusviisist, kus osalõikude [x_i−1, x_i] maksimaalne pikkus on λ. Kui eksisteerib piirväärtus

\lim _{\lambda \to 0}\sigma =\lim _{\lambda \to 0}\sum _{i=1}^{n}f(t_{i})\Delta _{i}.

mis ei sõltu lõigu [a; b] osalõikudeks jaotamise viisist ja punktide t_i valikust, siis kõneldakse, et funktsioon f(x) on integreeruv (Riemanni mõttes) lõigus [a; b] .

Vaata ka