Youngi katse
Youngi katse ehk kahe pilu katse on optikas eksperiment, mis demonstreerib asjaolu, et valgusel võivad olla nii laine kui ka osakese omadused, ning viitab ka kvantmehaaniliste nähtuste olemasolule.
Ajalugu ja üldine ettekujutus[muuda | muuda lähteteksti]

Youngi katse on nime saanud inglise teadlase Thomas Youngi (1773–1829) järgi. 19. sajandi alguses (1802. aastal) konstrueeritud Youngi katse nägi välja järgmiselt. Pimedas ruumis oli aknakattesse tehtud üks pisike ümmargune auk, millele langes loomulik päikesevalgus. Pilu läbimõõt oli ligikaudu 1 mm. Pilult langes kiirtekimp väikese plaadi servale, mille paksus oli pisut väiksem pilu läbimõõdust ehk kiirtekimbu laiusest. Õhuke plaat jagas langenud valguse kaheks ning neid plaadi servasid, kus valguse jagunemine toimus, võib vaadelda kui uute lainete allikaid. Nende lainete liitumisel tekkisid ekraanile tumedad ja heledad ribad ehk tekkis interferentsipilt (interferentsipildi tekkimine on kujutatud alloleval joonisel A).[1]
Hilisem ja tuntum versioon sellest katsest on aga järgmine. Koherentne valgusallikas valgustab õhukest plaati, milles on kaks paralleelset pilu. Pilusid läbinud valgust registreeritakse õhukese plaadi taga oleval ekraanil. Kui valgusel oleks vaid osakese omadused, siis võiks arvata et ekraanile tekiksid pilude kujutised ehk nende projektsioonid (olukorda kirjeldab allolev joonis B). Kuna pärast pilude läbimist tekivad tegelikult ekraanile tumedad ja heledad ribad ehk tekib interferentsipilt, siis see viitab asjaolule, et valgusel on laine omadused (olukorda kirjeldab joonis A).
Valguse laineomadusi saab jälgida ka ühe pilu abil. Katse sooritamiseks peab panema kaks sõrme kokku nii, et nende vahelt on veel vaevu valgust näha. Hoides näppe silmale lähedal ja vaadates seejärel mingit valgusallikat (näiteks lambipirni), on näha, et näppude vahele tekivad nendega paralleelsed, peenikesed tumedad ribad. Nähtavad tumedad ribad ongi ühe pilu korral tekkiva difraktsioonipildi miinimumid, mis viitavadki valguse laineomadustele.

Katse selgitus klassikalise laineoptika abil[muuda | muuda lähteteksti]
Sageli piisab valguse leviku kirjeldamiseks klassikalise laineteooria mudelitest. Näiteks Huygensi-Fresneli printsiip väidab, et lainefrondi iga punkt on sfäärilise laine allikaks ja uus lainefront tekib sekundaarlainete liitumisel. Liitumisel muutuvad nii faas kui ka iga laine amplituud, seega muutub samuti valguse intensiivsus.
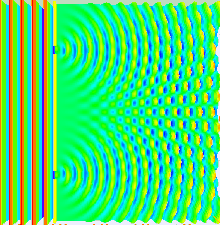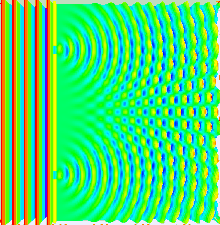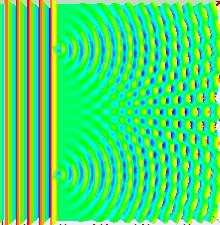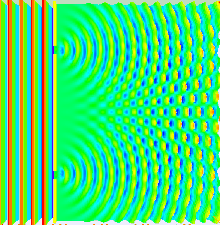
Youngi katset saab selgitada Huygensi-Fresneli printsiibi abil. Kui Youngi katse puhul tekib interferentsipilt kahe ava või pilu poolt lainefrondist eraldatud piirkondadest tulevate lainete liitumisel, siis Huygensi-Fresneli printsiibi korral on kogu ruum jagatud mõttelisteks avadeks (mis on kitsaste pilude erijuhuks), mis asuvad eraldamatult üksteise kõrval ning leviv lainefront moodustub neilt piludelt lähtuvate ligilähedaselt sfääriliste lainete liitumise tulemusena. Kahe pilu katses valgustatakse pilusid laserkiirega (tasalaine) ja piludest väljuvad silindrilised lained, mis omavahel interfereeruvad. Pilude vaheline kaugus on samas suurusjärgus valguse lainepikkusega. Kahe pilu süsteemi taha paigutatud ekraanile tekib interferentsipilt, mis tekib lainete faaside vahedest eri ruumipunktides ehk asjaolust, et lainete levimise teepikkused kindlasse punkti on erinevad. Interferentsipildi maksimumid tekivad ekraani nendes punktides, kus lained on samas faasis ja lainete amplituudid liituvad (valguse intensiivsus on maksimaalne). Nendes punktides, kus lained on vastandfaasis, tekivad interferentsipildi miinimumid.
Vaatame mõlemast pilust väljuvat samas faasis olevat kahte kiirt, mis levivad ekraanil olevasse punkti P. Nende käiguvahe avaldub:
kus
Siin r1 ja r2 on vastavalt esimeselt ja teiselt pilult tulevate kiirte teepikkused ekraanil oleva punktini P. S1 ja S2 on esimese ja teise pilu asukohad, mida võime vaadata kui uute lainete allikaid. B on teisele pilule kõige lähemal asuv punkt sirgel S1P, a on pilude vaheline kaugus ning θ on nurk lõigu S2B ja pilusid ühendava tasandi vahel.

Piludevaheline kaugus on võrreldes ekraani kaugusega väga väike. Seega
- ja
Paneme tähele, et
- ja samuti
Eeldame, et punkti P jõudes kiirte amplituudid liituvad ehk ekraanile punktis P tekib m-ndat järku interferentsi maksimum:
Kasutades ka eelmist seost, saab leida m-nda maksimumi kauguse punktist O:
Viimastes seostes on lisaks eelnevalt defineeritud tähistustele s ekraani kaugus piludest, O on ekraani keskpunkt, y on ekraanil oleva punkti P kaugus punktist O, m on interferentsi maksimumi järgu arv, ym on m-nda maksimumi kaugus punktist O ning λ on piludele langeva valguse lainepikkus.[3]
Katsete variatsioonid[muuda | muuda lähteteksti]
Üksikute osakeste interferents[muuda | muuda lähteteksti]

Youngi katse ühes tähtsamas variatsioonis saadetakse osakesi (või laineid) ühekaupa läbi kahe piluga konstruktsiooni, mille järel ilmuvad need ekraanile. Kui lasta nendel osakestel ükshaaval ekraanile kuhjuda, siis on näha seal interferentsipildi tekkimist (osakeste kuhjumist on kirjeldatud paremal oleval joonisel). Kui näiteks läbi topeltpilu suudetaks kontrollitult tulistada korraga ainult üks elektron,[4] võib interferentsipildist järeldada, et iga elektron on interfeerunud iseendaga ja seega pidi iga elektron korraga läbima mõlemat pilu.[5] See väide on vastuolus meie tavapärase arusaamaga objektide olemusest. Sama nähtust on suudetud katsega näidata ka aatomite ja mõnede molekulide puhul. Näiteks sfääriline fullereeni molekul on üks suuremaid molekule, mille korral see katse on veel edukalt läbi viidud.[6] Põhimõtteliselt interfereeruvad küll mistahes molekulide leiulained (lainefunktsioonid), kuid teatud suurusest alates pole mainitud efekt enam registreeritav. Katsed kinnitavad Diraci käsitlust, et elektronid, prootonid, neutronid ja suuremad ühendid, mida üldiselt nimetatakse osakesteks, on sellest hoolimata lainelise olemusega ja eriomase sagedusega.
Kirjeldatud katseline tulemus on väga hästi reprodutseeritav ning kvantmehaanika matemaatilised reeglid lubavad väga täpselt ennustada tõenäosust, et elektron ekraani mingit teatud piirkonda tabab. Sellegipoolest ei ole ennustatav elektronide ekraanile jõudmise järjekord – teadmine, mis ekraani piirkonda elektronid tabavad ja mis järjekorras eelnevad seda teinud on, ei anna alust öelda, kuhu satub iga järgmine elektron, kuigi on võimalik leida selle tõenäosusi eri piirkondades.[7] Teineteist ei võimenda ega kustuta mitte detektori eri punktides ilmuvate elektronide tõenäosused, vaid amplituudid, kuna tõenäosus on amplituudi ruut. Kui mingis piirkonnas lained teineteist kustutavad, ei tähenda see, et elektron kaob. Selle kadumine näitab elektroni teatud piirkonnas leidumise tõenäosuse vähenemist ja samal ajal kasvab võimalus leida see kusagilt mujalt.
Osakeste detektorid piludel[muuda | muuda lähteteksti]
Kahe pilu konstruktsiooni saab muuta, lisades piludele osakeste detektorid. See võimaldab katse läbiviijal kindlaks teha osakese asukoha juba siis, kui see topeltpilu läbib ja näha, kas toimus läbiminek ühest pilust, nagu osakeselt oodata võiks, või mõlemast, mida võiks eeldada laine korral. Paljudest varasematest katsetest on leitud, et ükskõik millised katseseadmele tehtud muudatused vähendavad ekraanil ilmuva interferentsipildi nähtavust,[8] mis illustreerib komplementaarsusprintsiipi: valgus, elektronid jne võivad käituda kas osakeste või lainetena, kuid mitte mõlemat korraga.[9]
1987. aastal tehtud katse tulemused näitavad aga, et teavet osakese kohta on võimalik saada sõltuvalt sellest, millise tee osake on valinud, hävitamata kogu interferentsi. 2012. aastal suudeti viimaks iga osakese poolt läbitud rada kindlaks teha interferentsi mõjutamata.[10] Selle saavutamiseks kasutati katseskeemi, kus ekraani tabavad osakesed ei tulnud mitte punktallikast, vaid kahe intensiivsusmaksimumiga allikast.
Viivitusega valik ja kvantkustutamise variatsioonid[muuda | muuda lähteteksti]
Viivitusega valiku katse ja kvantkustutamine on variatsioonid ühe osakese interferentsi eksperimendist, kus detektorid ei asu mitte piludel, vaid kusagil mujal katseskeemis.

Viivitusega valiku katsete puhul toimub otsustamine, kas soovitakse vaadelda interferentsi või infot valitud raja kohta, pärast seda, kui footon on juba topeltpilu läbinud. Tegu on John Archibald Wheeleri mõtteeksperimendiga, mille eesmärgiks on näidata, et footon "ei tea", kas ta tulevikus muutub interferentsipildi osaks või satub detektorisse, mis määrab ära, kummast pilust ta läbi läks.[11] Mõtteeksperimendi tulemused on ka tegeliku eksperimendiga korduvalt kinnitatud. Eksperimendis kasutatakse topeltpilu asemel ka Machi-Zehnderi interferomeetrit.[12][13][14]
Kvantkustutamine on eksperiment, mis näitab, et käitumine lainena on taastatav "valitud raja" informatsiooni kustutades või muud moodi kättesaamatuks tehes. Eksperiment kasutab põimolekus footonit, mõjutamaks juba pilu läbinud kaaslast.[15]
Neid katseid on võimalik kombineerida.[16] Sel juhul on tegu viivitusega valikuga kvantkustutamisega. Antud katse korral jaotatakse topeltpilu läbinud footon kaheks põimolekus footonite kimbuks. Ühel detektoril registreeritakse kõik footonid ühest kimbust, teise puhul toimub aga juhuslik valik (poolläbipaistvate peeglite abil) nelja detektori vahel, millest kaks on kättesaadavad mõlemat pilu läbinud footonitele (puudub informatsioon läbitud pilu kohta) ning kaks vaid ühest pilust pärit footonitele (sisaldab rajainformatsiooni). Oluline on siinkohal, et esimese kimbu läbitav teepikkus võib olla oluliselt lühem, kui teise oma; see tähendab et esimese kimbu footonid on jõudnud ekraanile enne, kui toimub valik teise kimbu ekraanide vahel. Kui nüüd vaadata teise kimbu ekraanidele langenud footonite paariliste asukohti esimese kimbu ekraanil, siis nende footonite paarilised, mis langesid ühistele ekraanidele, moodustavad interferentsipildi, ent nende footonite paarilised, mis langesid vaid üht pilu tuvastavatele ekraanidele, interferentsipilti ei moodustanud. See viitab sellele, et esimese kimbu footon langes kohe "õigele kohale", enne kui oli teada, kas tema paarilise puhul tehakse kindlaks läbitud teekond või mitte.
Viited[muuda | muuda lähteteksti]
- ↑ Walter Scheider. "Do the "Double Slit" Experiment the Way it Was Originally Done" (inglise). Vaadatud 19. mail 2013.
- ↑ "Young's Double Slit Experiment" (inglise). Vaadatud 19. mail 2013.
- ↑ Eugene Hecht (2002). Optics. 4th ed, 393–396
- ↑ O. Donati, G. F. Missiroli, G. Pozzi (1973). An Experiment on Electron Interference. American Journal of Physics 41:639–644
- ↑ Brian Greene, The Elegant Universe, lk 110
- ↑ O. Nairz, M. Arndt, ja A. Zeilinger. Kvanttaseme interferentsi katsed suurte molekulidega. American Journal of Physics, 2003; 71:319–325.
- ↑ Brian Greene, The Elegant Universe, lk 104 ja lk 109–114
- ↑ R. Feynman,R. Leighton, M. SandsMissiroli (1965). The Feynman Lectures on Physics, Volume III:Addison-Wesley lk 1–9
- ↑ D. Harrison (2002). Komplementaaarsusprintsiip ja Kopenhaageni tõlgendus kvantmehaanikast :Dept. of Physics, U. of Toronto
- ↑ Matthew Francis (22. mai 2012). "Disentangling the wave-particle duality in the double-slit experiment" (inglise). Vaadatud 19. mail 2013.
- ↑ J.A. Wheeler, W.H. Zurek (1983). Quantum Theory and Measurement. Princeton University Press. Lk 458.
- ↑ Roch; et al. (2007). "Experimental realization of Wheeler's delayed-choice GedankenExperiment". Science. 315 (5814): 966–968. DOI:10.1126/science.1136303.
{{cite journal}}: et al.-i üleliigne kasutus kohas:|author=(juhend) - ↑ O’Brien; et al. (november 2012). "A Quantum Delayed-Choice Experiment". Science. 338 (6107): 634–637. DOI:10.1126/science.1226719.
{{cite journal}}: et al.-i üleliigne kasutus kohas:|author=(juhend) - ↑ Tanzilli; et al. (november 2012). "Entanglement-Enabled Delayed-Choice Experiment". Science. 338 (6107): 637–640. DOI:10.1126/science.1226755.
{{cite journal}}: et al.-i üleliigne kasutus kohas:|author=(juhend) - ↑ Walborn; et al. (veebruar 2002). "Double-slit quantum eraser". Physical Review A. 65 (033818): 6. DOI:10.1103/PhysRevA.65.033818.
{{cite journal}}: et al.-i üleliigne kasutus kohas:|author=(juhend) - ↑ Yoon-Ho Kim,R. Yu, S.P. Kulik, Y.H. Shih ja M. Scully (2000). A Delayed Choice Quantum Eraser: Physical Review Letters 84: lk 1–5
Välislingid[muuda | muuda lähteteksti]
| Pildid, videod ja helifailid Commonsis: Youngi katse |








