Murdjoon

Murdjoon on elementaargeomeetrias kujund, mis koosneb otspunkte pidi järjestikku ühendatud lõikudest.
Murdjoon on lõikudest koosnev kujund, milles iga lõik on iga otspunkti kaudu ühendatud ülimalt ühe lõiguga ning kõik lõigud on omavahel otseselt või teiste lõikude kaudu ühenduses. Kui viimane tingimus ei ole täidetud, siis on tegu mitme murdjoonega.
Murdjoone mõiste on üldistatud reaalarvuliste kordajatega vektorruumidele.
Murdjoone mõistet rakendatakse muu hulgas geomeetrias, arvutusmatemaatikas, topoloogias, matemaatilises analüüsis, kompleksmuutuja funktsioonide teoorias, arvutigraafikas ja geodeesias.
Murdjooned Eukleidese ruumis[muuda | muuda lähteteksti]
Definitsioon[muuda | muuda lähteteksti]
Murdjooneks nimetatakse kujundit, mis koosneb lõikudest , , …, .
Punkte , … nimetatakse murdjoone tippudeks ja lõike , , …, murdjoone lülideks.
Murdjoonte tüübid[muuda | muuda lähteteksti]
Mittekõdunud ja kõdunud murdjooned[muuda | muuda lähteteksti]
- Murdjoont nimetatakse mittekõdunuks, kui mis tahes puhul lõigud и ei asetse ühel sirgel;
vastasel korral nimetatakse seda kõdunuks.
Tasandilised murdjooned[muuda | muuda lähteteksti]
Murdjoon on tasandiline, kui see asetseb tervikuna ühel tasandil.
Ennast lõikavad ja lihtsad murdjooned[muuda | muuda lähteteksti]
Murdjoon on ennast lõikav, kui sellel lеidub kaks lüli, millel on ühine punkt, mis ei ole nende ühine tipp:
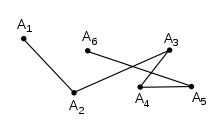
- Siin kujutatud murdjoont tuleb nimetada murdjooneks A1A2A3A4A5A6.
Murdjoont, mis ei ole ennast lõikav, nimetatakse lihtsaks.
Kinnised ja lahtised murdjooned[muuda | muuda lähteteksti]
Murdjoont nimetatakse kinniseks, kui selle esimene ja viimane punkt langevad kokku ning lõigud ja ei asetse ühel sirgel:

Kinnisel murdjoonel on iga lüli kummastki otsast seotud teise lüliga. N lülist koosneval kinnisel murdjoonel on N tippu.
Kinnist tasandilist murdjoont (või kujundit, mille äär on kinnine tasandiline murdjoon) nimetatakse hulknurgaks.[1]: sel juhul nimetatakse kujutatud murdjoont A1A2A3A4A5A1 hulknurgaks A1A2A3A4A5 ning selle lülisid hulknurga külgedeks. Mõnikord, näiteks hulktahukate käsitlemisel, nimetatakse hulknurga külgi servadeks.
Murdjoont, mille esimene ja viimane punkt on erinevad, nimetatakse lahtiseks. Lahtisel murdjoonel on kaks vaba otspunkti. N lülist koosneval lahtisel murdjoonel on N+1 tippu.
Rakendused[muuda | muuda lähteteksti]
Murdjooni rakendatakse näiteks andmepunktide interpoleerimisel, harilike diferentsiaalvõrrandite numbrilisel lahendamisel Euleri meetodil ning modelleerimisel arvutigraafikas ja raalprojekteerimises.
Märkused[muuda | muuda lähteteksti]
- ↑ Alternatiivselt nimetatakse hulknurgaks mis tahes kinnist murdjoont. Sel juhul eristatakse tasandilisi ja mittetasandilisi hulknurki.


![{\displaystyle [A_{1}A_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41bbcf9571621ee6021b17f0c44cd862f4cdd64a)
![{\displaystyle [A_{2}A_{3}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffbaf885fdbf4ffb0d9dbf73b56c4efd9967d889)
![{\displaystyle [A_{n-1}A_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/828b26ab37e3ffcbb9095df8609f2e8569cab721)



![{\displaystyle [A_{k}A_{k+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/961320625441d581f71ca463b3134f5ee4026fb6)
![{\displaystyle [A_{k+1}A_{k+2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cc68c105191b0ab8275f3901782399e0b06108e)

