Gibbsi vabaenergia
Gibbsi vabaenergia ehk Gibbsi energia, tähis G, on termodünaamiline potentsiaal, mis iseloomustab tööd, mida termodünaamiline süsteem suudab teha konstantsel temperatuuril ja rõhul. Sellest ka tema nimetus "vabaenergia" – energia, mis on töötamise jaoks "kätte saadav", n.ö "vaba". Gibbsi energia on võrdne maksimaalse kasuliku tööga, mida suudab teha suletud süsteem pöörduval protsessil ilma paisumistööta.
Gibbsi energia keemilise reaktsiooni jaoks on selle reaktsiooni toimumise potentsiaal, mis võrdub nulliga, kui reaktsioon on saavutanud tasakaalu.
Ajalugu[muuda | muuda lähteteksti]
Aastal 1873 publitseeris Josiah Willard Gibbs artikli pealkirjaga "A method of geometrical representation of the thermodynamic properties of substances by means of surfaces", milles ta tutvustas esmaseid põhimõtteid oma valemist, mis ennustas paljude protsesside kulgemist kehade või süsteemide kokkupuutel. Uurides erinevate homogeensete ainete interaktsioone kokkupuutel ning kasutades oma kolmemõõtmelist ruumala-entroopia-siseenergia graafikut, suutis Gibbs ennustada muutuste teket.
Algselt defineeriti Gibbsi energia graafiliselt. Gibbsi esimeses termodünaamika artiklis "Graphical Methods in the Thermodynamics of Fluids" (Graafilised meetodid vedelike termodünaamika uurimiseks) aastal 1873 kasutas ta koordinaattelgedena entroopia ning ruumala telgi, et väljendada keha olekut. Sama aasta lõpus kirjutas Gibbs artikli "A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces" (Meetod ainete termodünaamiliste omaduste geomeetriliseks väljenduseks pindade abil), kus ta lisas kolmanda telje, mis vastas keha siseenergiale. Järgmisel aastal kasutas James Clerk Maxwell Gibbsi graafikuid, et luua üks kolmemõõtmeline graafik entroopia, siseenergia ning ruumala telgedega.

Aastal 1882 väitis Hermann Ludwig Ferdinand von Helmholtz, et n.ö. "keemiline külgetõmbavus" on suurim võimalik töö, mida reaktsiooni suudab teha, kui see kulgeb pöörduval viisil, näiteks elektriline töö akus. Seda maksimaalset tööd käsitletakse kui süsteemi vaba, kättesaadava energia (Gibbsi vabaenergia, kui temperatuur ja rõhk on konstantsed ning Helmholtzi vabaenergia, kui temperatuur ja ruumala on konstantsed) vähenemisena, samas soojust, mis süsteemist väljub, käsitletakse süsteemi siseenergia vähenemisena. Seetõttu G või F iseloomustavad energiat, mis on "vaba" töö tegemiseks.
Järgneva 60 aasta jooksul asendati mõiste keemiline külgetõmbuvus mõistega vabaenergia. Aastal 1990 IUPACi väljastatud atmosfäärilise keemia mõistete sõnastikus[1] soovitati sõna "vaba" eemaldada, jättes ainult alles "Gibbsi energia".
Definitsioonid[muuda | muuda lähteteksti]
Gibbsi energia on defineeritud kujul
Konstantsel rõhul ja temperatuuril avaldub see valem nii
või
Kus:
- G on Gibbsi energia
- U on siseenergia
- p on rõhk
- V on ruumala
- T on temperatuur
- S on entroopia
- H on entalpia
Gibbsi energia kui kasulik töö[muuda | muuda lähteteksti]
Konstantsel temperatuuril ja rõhul on maksimaalne lisatöö (mittepaisumistöö), wadd,max, väljendatud kui muutus Gibbsi energias.[2]
Seda lisa tööd tähistatakse vastavalt sellele, mille jaoks seda tööd tehakse. Näiteks elektrilist tööd tehes on kasulik töö võrdne laenguga keha liigutamiseks kuluva energiaga zFE, kus z on osakese laeng, F on Faraday arv ning E on elektrivälja potentsiaal. Elektrilist tööd annab seetõttu väljendada ka Gibbsi energiaga:
Sellest valemist saab edasi arendada palju kasutatud Nernsti valemi.
Tuletus[2][muuda | muuda lähteteksti]
Kuna H = U + pV, siis üldine konditsioonide muutus toob kaasa entalpia muutuse:
Vastav muutus Gibbsi energias (G = H – TS) on
Kui muutus on isotermiline (dT = 0), siis
Kui muutus on pööratav ehk dw = dwrev ja dq = dqrev = TdS, siis muutub valem nii:
Töö koosneb paisumistööst, mis pöörduva muutuse korral väljendatakse –pdV-na, ning võimalusel mingisugusest lisatööst (näiteks patareis elektromotoorjõu tekitamine). Seda lisatööd märgime tähisega dwadd. Seetõttu, võttes d(pV) = pdV + Vdp,
Kui ka rõhk on konstantne, siis dp = 0 ning
Kuna protsess on pöörduv, on lisatöö maksimaalne.
- q on soojushulk
- w on töö
Reaktsioonide vaba energia[muuda | muuda lähteteksti]
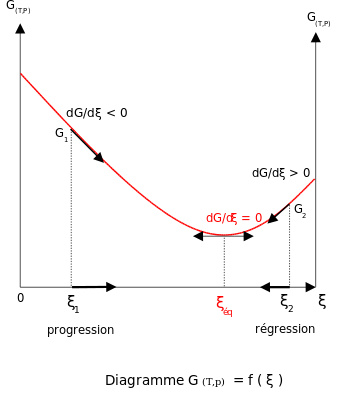
Üldine reegel on, et kõik süsteemid püüdlevad minimaalse energia poole. Seetõttu toimuvad ka reaktsioonid konstantsel temperatuuril ja rõhul sinna suunas, kus on väiksem energia. See energiamuutus, mis tänu reaktsioonile toimub, on reaktsiooni Gibbsi energia. Reaktsiooni Gibbsi energia arvutatakse järgmiselt:
Kui reaktsiooni Gibbsi energia muut (seda tähistab kolmnurk, delta) on negatiivne, toimub reaktsioon saaduste suunas, kui positiivne, siis lähteainete suunas ning kui Gibbsi energia on 0, siis reaktsioon on jõudnud tasakaaluolekusse ning reageerimine lõppeb. Reaktsioone liigitatakse Gibbsi energiat arvestades kas eksoergilisteks või endoergilisteks reaktsioonideks (kreeka keelest ergon, töö). Kui reaktsiooni läbi viimiseks on vaja teha tööd, on reaktsioon endoergiline, kui reaktsioon on võimeline tööd tegema, ehk reaktsioon kulgeb iseeneslikult, on reaktsioon eksoergiline.[3]
Juhul, kui reaktsiooni entalpia ning entroopia kohta andmed puuduvad, saab reaktsiooni Gibbsi energia arvutamiseks kasutada erinevatele ainetele iseloomulikku standardset formatsiooni Gibbsi energiat ning reaktsioonis osalevate ainete aktiivsusi.
Kus
- ΔrGo on standardne reaktsiooni Gibbsi energia
- ΔrG on reaktsiooni Gibbsi energia
- R on universaalne gaasi konstant
- T on absoluutne temperatuur
- Q on saaduste aktiivsuste ning lähteainete aktiivsuste jagatis.
Eelmise valemi abil on võimalik leida reaktsiooni tasakaalukonstanti, kuna tasakaalu korral Q = Kα ning ΔrG = 0. Paneme muudatused valemisse ning saame reaktsiooni standardse Gibbsi energia valemi tasakaalukonstandi Ka-ga.
Tuletus[4][muuda | muuda lähteteksti]
Võtame näitena reaktsiooni, kus aine A muutub aineks B
Oletame, et infinitesimaalne hulk dξ ainet A muutub aineks B. Aine A hulga muutus oleks dnA = – νA dξ ning aine B hulga muutus oleks dnB = + νB dξ, kus ξ on reaktsiooni kulg ning ν on stöhhiomeetriline kordaja. Reaktsiooni Gibbsi energiat saab defineerida ka kui tõus Gibbsi energia ning reaktsiooni kulgemise graafikul.
Me teame veel, et konstantsel temperatuuril ja rõhul on Gibbsi energia võrdne reaktsioonis osalevate ainete keemiliste potentsiaalidega.
Asendades valemisse dξ, saame
ehk
Kasutades reaktsiooni Gibbsi energia valemit
Keemiline potentsiaal on seotud vastava elemendi aktiivsusega a.
Asendades keemilised potentsiaalid antud valemiga, saame
- ΔrG on reaktsiooni Gibbsi energia
- ΔrGo on standardne reaktsiooni Gibbsi energia
- ξ on reaktsiooni kulg
- n on aine hulk
- ν on ainete stöhhiomeetriline kordaja reaktsioonis
- μ on keemiline potentsiaal
- μo on standardne keemiline potentsiaal
- R on universaalne gaasikonstant
- T on absoluutne temperatuur
- a on aine aktiivsus lahuses
Standardne formatsiooni Gibbsi energia[muuda | muuda lähteteksti]
Aine standardne formatsiooni Gibbsi energia on Gibbsi energia muut 1 mooli selle aine kujunemisel selle aine komponentidest standardolekus. Kõikidel elementidel nende standardolekus on formatsiooni Gibbsi energia 0, kuna nad on juba standardolekus.
Standardne formatsiooni Gibbsi energia on kasulik reaktsiooni suuna ennustamiseks standardtingimustel (rõhk on 1 bar ning temperatuur 25 kraadi Celsiuse järgi): reaktsioon liigub alati madalaima energiakoguse suunas.
Valik ainete standardsetest formatsiooni Gibbsi energiatest[5][muuda | muuda lähteteksti]
| Aine | Olek | ΔfG°(kJ/mol) |
|---|---|---|
| NO | gaas | 87,6 |
| NO2 | gaas | 51,3 |
| N2O | gaas | 103,7 |
| H2O | gaas | −228,6 |
| H2O | vedel | −237,1 |
| CO2 | gaas | −394,4 |
| CO | gaas | −137,2 |
| CH4 | gaas | −50,5 |
| C2H6 | gaas | −32,9 |
| C3H8 | gaas | −23,4 |
| C6H6 | gaas | 129,7 |
| C6H6 | vedel | 124,5 |
Viited[muuda | muuda lähteteksti]
- ↑ International Union of Pure and Applied Chemistry (IUPAC) atmosfäärilise keemia komisjon, J. G. Calvert. "Glossary of Atmospheric Chemistry Terms (Recommendations 1990)". Pure Appl. Chem., vol. 62 (11), lk 2190, 1990
- ↑ 2,0 2,1 P. Atkins, J. De Paula (2006). Atkins’ Physical Chemistry. 8. Köide. Lk 99
- ↑ K. J. Laidler, J. H. Meiser, B. C. Sanctuary, 2003, "Physical Chemistry", 4. väljaanne, lk 125–126
- ↑ K. J. Laidler, J. H. Meiser, B. C. Sanctuary, 2003, "Physical Chemistry", 4. väljaanne, lk 205
- ↑ CRC Handbook of Chemistry and Physics, 2009, pp. 5–4 – 5–42, 90th ed., Lide
Välislingid[muuda | muuda lähteteksti]
- PDF fail "Puhaste ainete vaba energia ja keemiline potentsiaal"
- "Kord, korrastus ja entroopia"
- Ingliskeelne seletus reaktsiooni tasakaalu kohta
- Gibbsi energia ning reaktsiooni spontaansus Khanacademy (inglise keeles)
- Gibbsi energia Bozeman science (inglise keeles)






















