Optiline sihik
Optiline sihik (kõnekeeles optika; inglise keele eeskujul vahel ka teleskoopsihik) on optiline vahend üle pika vahemaa nägemiseks, enamasti märgib see teleskoopi, mis on kinnitatud täpsusrelvale. Optilise sihiku suur nägemisulatus on saavutatud mitmete läätsedega. Pildi kvaliteet sõltub aga ka läätsede kvaliteedist ja kattest. Lisaks optilisele sihikule on kasutuses ka kirp ehk raudsihik, lasersihik ja peegelsihik.
Kirjeldamine
[muuda | muuda lähteteksti]
Sihikud on tavaliselt disainitud eesmärgipõhiselt (valgustatus, kaugus) jaoks. Need kasutamistingimused omakorda seavad nõudmised teleskoopsihiku omadustele. Näiteks sihikud, millega vaadatakse kilomeetri kaugusele, omavad enamasti suurt objektiivi, et tekitada heledamat kujutist. Kuna suurema läbimõõduga läätse läbib rohkem valgust, siis saab suurema läätsega valgustatuma pildi kui väiksemat läätse kasutades. Teleskoopsihikuid eristatakse enamasti nende suurenduse ja objektiivi läbimõõdu järgi. Kui teleskoopsihikul on näiteks kirjelduseks 10x50 tähendab see, et sihik annab 10 kordse suurenduse 50 mm-se läätsega, ehk siis sihiku kirjeldus antakse enamus olukordades nende kahe arvu kombinatsioonina, kus esimene liige näitab suurendust ja teine näitab läätse läbimõõtu millimeetrites. Samas vahel kohtab kirjelduses ka vahemikke. See viitab muudetavale suurendusele ning sellisel juhul on kirjelduses antud minimaalne ja maksimaalne suurendus ning läätse läbimõõt. Mõnevõrra üllataval kombel suurendab suurem läätse läbimõõt ka pildi teravust, kuna vastavalt Rayleigh' kriteeriumile tekib sihikust vaadeldava eseme punktilt valguse difraktsiooni tõttu suuremalt läätselt väiksem Airy ketas, mis tähendabki teravamat pilti. Praktikas ei ole enamus juhtudel vaja Rayleigh' kriteeriumiga arvestada, sest enamasti halvendab pildi teravust sihikus kasutatava optika kvaliteet. Samas kui lääts omab tühiseid aberratsioone ja optiliselt sihikult nõutakse väga suurt lahutusvõimet, on vaja arvestada Rayleigh' kriteeriumiga.
Parandid
[muuda | muuda lähteteksti]Kui relvaga lastakse kaugele, siis mõjub kuulile lennu ajal Maa raskusjõud. Kui mõelda, et kuul lendab horisontaalselt 1000 meetri kaugusele keskmise kiirusega 1000 m/s (kuuli kiirus väheneb lennu ajal õhutakistuse mõjul), siis viibib ta vabalangemises ühe sekundi jooksul. Selle aja jooksul jõuab kuul vertikaalselt langeda 5 meetri võrra. See on aga juba küllaltki suur langus, et laskur ei saaks ilma sihtimise paranduseta vastasele pihta. Et kuuli langemist kompenseerida, on teleskoopsihiku niitristi vertikaalse joone peale horisontaalsed kriipsud, mille järgi saab hinnata sihtmärgi kaugust. Neid kriipse nimetatakse kaugusjoonteks. Horisontaalsel niitristi joonel on vertikaalsed jooned või täpid mis aitavad tuule mõju kompenseerida. Tuulejoonte korral tuleb tuule kiirus küll ise mõõta.
Tuhandikpunktisüsteem
[muuda | muuda lähteteksti]Tuhandikpunktisüsteem (Mil-dot system; MIL-süsteem) on üks võimalikest kaugusjoonte süsteemidest.
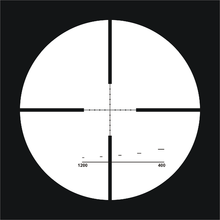
Mil-dot paigutusega sihikud on väga kasulikud tulistamiskauguse kiireks väljaarvutamiseks. Snaiprid kasutavad mil-dot sihikut, et määramata kaugust sihtmärgini. Samuti saab mil-dot sihiku jooni kasutada alternatiivsete sihtimispunktidena [1].
MIL-süsteemi taga peituv matemaatika on suhteliselt lihtne. Kui vaadata kaugusel asuvat objekti kõrgusega läbi optilise sihiku, siis objekt omab ka mingisugust nurkläbimõõtu . Nurka , kaugust objektini ja eseme kõrgust seob matemaatiline seos . Üheks levinud standardiks on kasutada objekti kauguseks 1000 meetrit ning objekti kõrguseks 1 meetrit - kui sellisel juhul paigutada ese sihiku vaatevälja nii, et eseme üks ots asub sihiku horisontaalse joone peal, siis vaadeldav objekt mahub sihiku horisontaalse joone ja esimese Mil-dot joone vahele. Nurkläbimõõt eelpool mainitud kauguste jaoks oleks: . Kuna saadud nurga suurus radiaanides on väga väike võib kasutada lähendust ning meie esialgne seos võtab kuju . Asendades nurga Mil-doti joonte arvuga saame seose , mis on vägagi mugav kiireks vahemaade arvutamiseks.
Näide tuhandikpunktisüsteemi kasutamisest
[muuda | muuda lähteteksti]Ülesanne: Juhani pikkus on ja ta mahub ära Mil-dot punkti vahele. Kui suurel kaugusel on Juhan?
Lahendus: Kui Juhan oleks kaugusel mahuks ta ära punkti vahele. Saame seose
Vastus: Juhan on 460 meetri kaugusel.
Vaata ka
[muuda | muuda lähteteksti]
Viited
[muuda | muuda lähteteksti]Välislingid
[muuda | muuda lähteteksti]| Pildid, videod ja helifailid Commonsis: Optiline sihik |














