Regulaarne graaf

Regulaarne graaf on graaf mille kõikide tippude valentsused (astakud) on võrdsed, st iga tipp omab sama arv naabertippe.

Regulaarsuse valents on graafi invariant ning tähistatakse $r(G)$. Kõikide graafide hulgas domineerivad mitteregulaarsed, regulaarsete osakaal on kaduvväike. Kuna regulaarsete graafide raames võib esineda ka teisi regulaarsusi, siis nimetagem siin esimest valentsregulaarsuseks.

Valentsuse (astaku) järgi klassifitseeritult koosneb: 0-regulaarne (tühi graaf) isoleeritud tippudest; 1-regulaarne isoleeritud servadest; 2-regulaarne isoleeritud ringidest (tsüklitest, vöödest) või kujutab tervikuna ringi. 3-regulaarset nimetatakse ka kuupgraafiks.

• 
  0-valentsregulaarne graaf
• 
  1-valentsregulaarne graaf
• 
  2-valentsregulaarne graaf
• 
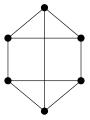
  3-valentsregulaarne graaf

Täiendavad regulaarsused

Graafi regulaarsus on tippude ja/või servade omadus olla teatud mõttes ühesugused. On olemas erinevaid regulaarsusi.

• Valentsregulaarne graaf, mille iga tipu kõikide naabertippude kaugus on d, on d-distantsregulaarne. Näites esitatud 3-valentsregulaarne graaf on ka 2-distantsregulaarne.
• Valentsregulaarne graaf, mille kõik tipud kuuluvad vöösse ümbermõõduga d on d-vööregulaarne. Näiteks, valentsregulaarne Peterseni graaf on 5-vööregulaarne.
• Valentsregulaarne graaf, mille kõik tipud kuuluvad klikki võimsusega n on n-klikkregulaarne. Näiteks, Peterseni graafi täiend on 4-klikkregulaarne ning koosneb neljast lõikuvast 4-klikist.
• Valentsregulaarne graaf, mille iga naabertippude paar omab $a\geqslant 0$ ühist naabrit ja iga mittenaabertippude paar omab $b\geqslant 1$ ühist naabrit on tugevregulaarne. Näiteks, Peterseni graaf on ka tugevregulaarne.

Need regulaarsused on hästi väljaloetavad graafi semiootilisest mudelist.

Seoseid regulaarsuste vahel

• Valentsregulaarsete graafide hulgas on distants-, vöö-, klikk- ja tugevregulaarsete osakaal kaduvväike.
• Valentsregulaarse graafi $r(G)$ täiend ${\overline {G}}$ on valentsregulaarne.
• Vööregulaarse graafi $G$ täiend ${\overline {G}}$ on klikkregulaarne, ja vastupidi.
• Klikkregulaarse graafi klikid võivad olla kas komponentsed, sidusad või lõikuvad.
• m-aluselise graafi $G$ täiend ${\overline {G}}$ on võrdsete aluste n puhul n-klikkregulaarne, mittelõikuvate n-klikkide arvuga m.
• Tugevregulaarse graafi $G$ sidus täiend ${\overline {G}}$ on tugevregulaarne.

Regulaarsus ja sümmeetria

Ka graafi sümmeetria puhul on tegemist ühesuguste kordumisega ehk ekvivalentsusklassidega. Graafi sümmeetria on nö "kõige tugevam regulaarsus". Tippudest sümmeetriline (transitiivne) graaf on valents-, distants- ja vööregulaarne (või klikkregulaarne) . Samal ajal on valentsregulaarne graaf väga harvadel juhtudel sümmeetriline. Ka tugevregulaarne graaf ei pea olema sümmeetriline.

Kirjandust

• Harary, F. Graph Theory. Addison-Wesley, 1969.
• Tevet, J.-T. Graafi varjatud külgi. S.E.R.R. 2009. ISBN 9789949213108
• Ashay Dharwadker, A., Pirzada, B. Graph Theory, Proc. Institute of Mathematics, Amazon Books, 2011. ISBN 1466254998

Vaata ka

Graafi klikk ja vöö