Ühisteguriteta arvud

Ühisteguriteta arvud on täisarvud $A$ ja $B$, mille ainus ühistegur on arv 1. Sellest järeldub, et ükskõik milline algarv, mis jagub esimene täisarvu, ei jaga teise täisarvu.

Täisarvud $a$ ja $b$ on ühisteguriteta arvud kui nende suurim ühistegur (GCD) on $1$.

Lugeja ja nimetaja taandatud murruosas on ühisteguriteta arvud. Näiteks $2,3$ on ühisteguriteta arvud, sest mõlemad arvud jaguvad $1$-ga. $10,15$ ei ole ühisteguriteta arvud, sest neid saab jagada $5$-ga. $3,4,11$ on ühisteguriteta arvud, sest ei leidu ühistegurit, mis ei ole 1 ja mis jagab kõik kolm numbrit.

Ühisteguriteta arvude $a$ ja $b$ standardne esitus on $gcd(a,b)=1$ ja $(a,b)=1$ . GCD leidmiseks saab kasutada Eukleidese algoritmi.

Kui $a$ ja $b$ on ühisteguriteta arvud ja $gcd(a,b)=1$, siis nende notatisoon on $a\perp b$.

Ühisteguriteta arvud hulkadel

Hulk $H=\{a_{1},a_{2},...a_{n}\}$, kus $a_{n}$on täisarvud, saab olla ühisteguriteta hulk või kindlalt ühisteguriteta, kui hulga elementide suurim ühistegur on 1. Näiteks hulk, mille elemendid on $7,9,13$ on ühisteguriteta arvud, sest ei leidu ühistegurit, mis ei ole $1$ ja mis jagab kõik numbrid ja sellest järeldub, et hulk on kindlalt ühisteguriteta.

Kui täisarvude hulgas on kaks suvalist täisarvu ühisteguriteta arvud, siis need arvud on paarikaupa ühisteguriteta arvud ja hulk on paarikaupa ühisteguriteta hulk. Hulgas ${6,7,9}$ leidub kaks arvu, kus iga arv on ühisteguriteta arv $(6,7)$, aga kõik hulga elemendid pole paarikaupa ühisteguriteta arvud, sest $6,9$ ei ole ühisteguriteta arv. Iga paarikaupa ühisteguriteta hulk, mis on lõplik, on kindlalt ühisteguriteta hulk, aga kindlalt ühisteguriteta hulk ei ole paarikaupa ühisteguriteta hulk.

Lõpmatu hulga elemendid on ühisteguriteta arvud, kui kõik hulga elemendid on $a_{n}=a_{1}...a_{n}+1$.

Paarikaupa ühisteguriteta arvud saavad olla lõpmatu hulgas. Märkimisväärsed näited on hulk Sylvester'i jadas, kus kõik elemendid on Fermat' arvud ja hulk, kus kõik elemendid on Mersenne'i arvud.

Omadused

Kui $a$ ja $b$ on ühisteguriteta arvud, siis järgmised tingimused on samaväärsed:

• Ei leidu algarvu, mis jagub $a$ ja $b$.
• Leiduvad täisarvud $x$ ja $y$ nii, et $ax+by=1$ (Bézout'i identiteet).
• Arvude $a$ ja $b$ vähim ühiskordne on $ab$.
• Kui $a$ on $bc$ jagaja ning $a$ ja $b$ on ühisteguriteta arvud, siis $a$ on $c$ jagaja.

Esimesest punktist järeldub, et $a^{k}$ja $b^{m}$ on ühisteguriteta arvud.

Pilt 1. 4 ja 9 on ühisteguriteta arvud. Seetõttu diagonaal ei sisalda tippe täisarvu koordinaatidega

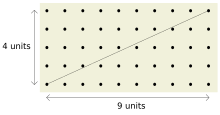
Täisarvud $a$ ja $b$ on ühisteguriteta arvud siis ja ainult siis, kui diagonaal punktist $(0,0)$ punkti $(a,b)$ Descarter’i koordinaatsüsteemis ei sisalda tippe täisarvu koordinaatidega (vt Pilt 1).

Kaks naturaalarvu $a$ ja $b$ on ühisteguriteta arvud siis ja ainult siis, kui numbrid $2^{a}-1$ ja $2^{b}-1$ on ühisteguriteta arvud.

Ühisteguriteta arvu tõenäosus

Oletame, et on täisarvud $a$ ja $b$, ja tahame leida tõenäosus, et mõlemad arvud on ühistegurite arvud.

Oletame, et $q$ on tõenäosus sellest, et kaks juhuslikult valitud täisarvud on ühisteguriteta arvud. Oletame, et oli võetud juhuslikult valitud täisarv $k$. Tõenäosus sellest, et $k$ jagub $a$ on ${\frac {1}{k}}$ . Tõenäosus sellest, et $k$ jagub $b$ on sama. Sellest järeldub, et tõenäosus sellest, et $k$ jagub $a$ ja $b$ on ${\frac {1}{k^{2}}}$. Tõenäosus sellest, et $gcd({\frac {a}{k}},{\frac {b}{k}})=1$ on $q$, aga $gcd({\frac {a}{k}},{\frac {b}{k}})=1$ ja $gcd(a,b)=k$ on samaväärsed. Kui oletada, et on sündmuste sõltumatus, siis tõenäosus, et $gcd(a,b)=k$ on ${\frac {1}{k^{2}}}\centerdot q={\frac {q}{k^{2}}}$. Sest sündmused $gcd(a,b)$ on üksteist välistavad ja tõenäosus sellest, et on $gcd$ on $1$ järeldub järgmisele:

$1=\sum _{k=1}^{\infty }{\frac {q}{k^{2}}}$, mis tähendab, et $q=[\sum _{k=1}^{\infty }{\frac {1}{k^{2}}}]^{-1}={\frac {6}{\pi ^{2}}}$.

Vastastikuste algarvude paaride genereerimine

Kõik positiivsete vastastikuste algarvude paarid $(m,n)$, kus $m>n$, saab organiseerida kahe tähelised puudega, kus puul iga tipu lehtede arv on väiksem kui $4$. Üks puu algus on punktis $(2,1)$ (kõik paaris-paaritu ja paaritu-paaris paarid) ja teise puu alguspunkt on $(3,1)$(kõik paaritu-paaritu paarid). Iga veeru $(m,n)$ lehed genereeritakse nii:

• Serv 1: $(2m-n,m)$
• Serv 2: $(2m+m,m)$
• Serv 3: $(m+2n,n)$