Tunneliefekt
Tunneliefektiks ehk tunneleerumiseks nimetatakse mikroosakese läbiminekut potentsiaalibarjäärist. Tegemist on kvantmehaanika nähtusega, kus nt elektronid on suutelised läbima lõpliku paksuse ja kõrgusega potentsiaalibarjääri ehk potentsiaalse energia barjääri, sest omavad laineomadusi. Osakesed kas peegelduvad tagasi (tungides osaliselt barjääri sisse) või läbivad selle. Klassikalise teooria kohaselt on osakeste poolt barjääri läbimine võimatu. Mikroosakeste korral on see aga võimalik, olgugi et barjääri läbimise tõenäosus on üldiselt väike.[1][2]
Kui vaadelda elektroni, mis on ainelaine, siis on sel lõplik tõenäosus lekkida või imbuda (öeldakse ka: tunneleeruda) läbi barjääri ja ilmuda välja selle vastasküljel. Tunneleerumine toimub olukorras, kus elektroni potentsiaalne energia E on barjäärile lähenedes suurem kui barjääri enda kõrgus ehk barjääri potentsiaalne energia U0 (joonisel V0 ), st kui E > U0 , siis suudab elektron selle barjääri ületada.[1][2][3]

Võime vaadelda lõpliku laiusega potentsiaalibarjääri . Siin on potentsiaalibarjääri paksus. Piirkonnas x < 0 on barjäärile langevate ja sellelt peegeldunud osakeste voog, piirkonnas x > a saab olla vaid barjääri läbinud osakeste voog. Barjääri seest, piirkonnast 0 < x < a, on osakeste leidmise tõenäosus nullist erinev.
Tõenäosust iseloomustab tõenäosustihedus, mis leitakse Schrödingeri võrrandist arvutatud lainefunktsiooni abil; seega kasutatakse tunneliefekti olemasolu tõestamiseks Schrödingeri võrrandit.[2]
Osakeste läbiminekut potentsiaalibarjäärist iseloomustab barjääri läbilaskvuskoefitsient, mis üldiselt sõltub nii barjääri kõrgusest kui ka barjääri laiusest. Potentsiaalibarjäärile võib omistada ka ainelaine läbitavusteguri T, mis iseloomustab tunneleerumise tõenäosust.[4]
Rakendused[muuda | muuda lähteteksti]
Tunneliefekti tõttu esineb hulk nähtusi, mis klassikalise teooria järgi oleks võimatud. Tänu nendele nähtustele on tunneliefektil mitmeid olulisi tehnilisi rakendusi:

- Tunneliefektil on palju rakendusi tehnikas, näiteks tunneldioodis, mida elektronid läbivad tunneleerumise teel, mistõttu elektronide voogu saab kärmelt muuta potentsiaalibarjääri kõrguse muutmise kaudu. Seade on sobiv erilist kiiretoimelisust nõudvais rakendustes.[1][5]
- Üheks oluliseks nähtuseks loetakse elektronide külmemissiooni, kus elektronid saavad metallist väljuda ainult tunneliefekti tõttu, kui metall on asetatud välisesse elektrivälja. See nähtus vastandub termoemissioonile, kus metalli kuumutamisel saadud soojusliikumise energia ületab väljumistöö.[2] Elektronide külmemissioon on oluline nähtus pooljuht- ja ülijuhtmaterjalides, mis tänapäeval on tähtsal kohal välkmälude ja ka mõnede elektronmikroskoopide valmistamisel.[6]
- Tunneliefekt aitab kaasa ka tuumareaktsioonides, nt tuumade radioaktiivsel lagunemisel alfaosakeste tekkega (tuumade alfalagunemine) ja tuumade ühinemisel Päikese sisemuses ja vesinikupommis.[2]
Animatsioon tunneliefektist ja skaneeriva tunnelmikroskoobi (STM) tööpõhimõttest - Tunneliefektil rajaneb ka skaneeriv tunnelmikroskoop (STM) (vt tööpõhimõtte animatsiooni paremal), kus kasutatakse elektronide ainelaineid. Need palju lühemad lained ei haju pinnalt nii nagu valguslained optilises mikroskoobis, mistõttu on võimalik vaadelda palju väiksemaid detaile. Kujutis tekitatakse elektronidega, mis tunneleeruvad läbi potentsiaalibarjääride STM teravikul. Teraviku ja uuritava objekti pinna vahele on rakendatud nõrk elektripinge ( u 10 mV). Kui viia teravik küllalt lähedale, siis saavad elektronid uuritavast proovist läbi selle vahemiku (barjääri) tunneleeruda ning tunnelvoolu tekitada. Vool muutub tugevamaks, kui vahemaa pinna ja mikroskoobi otsa vahel väheneb. Kui mõõta tunnelvoolu suurust teraviku skaneerimisel objekti pinna kohal, on võimalik saada infot pinna-aatomite kohta. Vool muundatakse kõrguse arvutamise teel ning see annab materjali pinna nanomeetrilise tüpograafia – saadud videokujutise abil on näha uuritava proovi pinnareljeefi. Tunnelmikroskoobiga on võimalik ka aatomeid ja molekule mööda pinda nihutada. Tänapäeval toodetakse tunnelmikroskoope tööstuslikult ja neid kasutatakse paljudes laborites üle kogu maailma.[1][2]
Tunneliefekti alaliigid[muuda | muuda lähteteksti]
Tunneliefekti saab jaotada Schottky efektiks ja Fowler-Nordheimi efektiks. Fowler-Nordheimi tunneleerumine on kvantmehaanilise tunneliefekti nähtus, kus elektrostaatiline väli indutseerib metallist elektronide emissiooni teistesse kristallilistesse tahkistesse. Fowler-Nordheimi tunneliefektis vähendatakse elektriväljaga isoleeriva dielektrikukihi potentsiaalibarjääri laiust.
Ralph H. Fowler ja Lothar Wolfgang Nordheim olid esimesed, kes tulid välja ideega, et elektrostaatiline väli võib põhjustada sellist emissiooni ja kirjeldasid selle Schrödingeri võrrandist tuletatud valemitega. Nad lahendasid Schrödingeri valemi teravate või ümardatud nurkadega kolmnurkse potentsiaalibarjääri kohta. Saadud Fowler-Nordheimi valemeid kasutatakse ka kirjeldamaks väljaemissioone teistest materjalidest, kuid kõige täpsemini kirjeldavad need valemid siiski emissioone metallidest kristallidesse. Fowler-Nordheimi valemid on kõigest reaalse füüsilise efekti lähendused, kuna kui sisestada Schrödingeri valemisse realistlikumad potentsiaalibarjääri kujud, siis on saadud diferentsiaalvõrrandid analüütiliselt lahendamatud.
Fowler-Nordheimi efekti kasutatakse NAND-tüüpi välkmäluelementides transistori ujuvpaisule laengu kandmiseks ja seeläbi info salvestamiseks.
Schottky efekt aga kasutab elektrivälja, et potentsiaalibarjääri madaldada. Madalama potentsiaalibarjääri puhul suureneb tunneliefekti tõttu materjalide vaheliste elektronide voog.
Puudused[muuda | muuda lähteteksti]
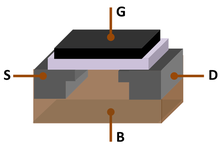
Moodsas tehnoloogias kasutatavate väljatransistoride puhul on oluliseks nende mõõtmete (ja ka nende komponentide mõõtmete) vähendamine. Et väljatransistor töötaks, peab elektrimahtuvus tema voolu juhtiva kanali ja voolu tüüriva elektroodi ehk paisu vahel olema piisavalt suur. Imelühikese kanalipikkuse juures peab kanalit ja paisu eraldav dielektrik olema väga õhuke, tagamaks vajalikku mahtuvust. Üliõhuke oksiidkiht metalloksiid-pooljuht-väljatransistori (MOSFET) (vt samanimelist joonist) komponendina vähendab transistoris lätet ja kanalit eraldava potentsiaalibarjääri laiust, mistõttu elektronidel on kergem tunneleeruda läbi isolaatorkihi. Traditsiooniliste väikese dielektrilise läbitavusega materjalide (nt ränidioksiidi, räninitriid) kasutamisel on nõutava kihi paksus (1–2 nm) liiga väike naaberaatomite vahelise kauguse (0,2–0,3 nm) tõttu. Nii õhukestes dielektrikutes hakkab mõjuma tunneliefekt, mis viib isoleerivate omaduste]] halvenemiseni tunnelvoolu tõttu. Selline tunnelvool võib olla ka seadme peamiseks lekkeallikaks – tekib lekkevool, mis põhjustab vigase vooluringi ja suurendab MOSFETi reservvõimsust.[7][8]
Ajalugu[muuda | muuda lähteteksti]
1973. aasta Nobeli füüsikaauhinda jagasid kolm "tunnelisti": Leo Esaki (tunnelnähtuste avastamise eest pooljuhtides), Ivar Giaver (tunnelnähtuste avastamise eest ülijuhtides) ja Brian Josephson, kes leiutas Josephsoni siirde – nobeda kvantlüliti, mille aluseks on taas tunneliefekt. 1986. aasta Nobeli auhinna said Gerd Binning ja Heinrich Rohrer samuti tunneliefektil rajaneva skaneeriva tunnelmikroskoobi loomise eest.[1][3]
Huvitavad faktid[muuda | muuda lähteteksti]
Efekti hakati nimetama just tunneliefektiks, kuna piltlikult kujutati barjääri läbimist nii, nagu läheks osake läbi barjääri sees oleva tunneli. See ettekujutus pole muidugi õige, sest mingit tunnelit barjääri ei teki.[2]
Viited[muuda | muuda lähteteksti]
- ↑ 1,0 1,1 1,2 1,3 1,4 Füüsika põhikursus. Teine köide. Halliday, Resnick, Walker. Lk 1068–1070.
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 2,6 Sissejuhatus kvantmehaanikasse. Rein-Karl Loide. 2007. Lk 48–50.
- ↑ 3,0 3,1 "Eksperimentaalmeetodid materjalifüüsikas, STM. Loengumaterjal" (PDF). Originaali (PDF) arhiivikoopia seisuga 11. juuni 2007. Vaadatud 12. jaanuaril 2014.
- ↑ "Tallinna Tehnikaülikool, Kaasaegne Füüsika I, loengumaterjalid". Originaali arhiivikoopia seisuga 1. oktoober 2011. Vaadatud 30. jaanuaril 2014.
- ↑ "Kvantmehaanika I. Tartu Ülikooli Füüsika Instituut. Loengumaterjalid. Lk 1–5" (PDF). Originaali (PDF) arhiivikoopia seisuga 1. veebruar 2014. Vaadatud 25. jaanuaril 2014.
- ↑ Taylor, J., Modern Physics for Scientists and Engineers, Prentice Hall, 2004. Lk 479.
- ↑ Chaudry, A. Fundamentals of Nanoscaled Field Effect Transistors. 2013, Springer, Chapter 2. Lk 26.
- ↑ Teadusmõte Eestis. Täppisteadused. Ilmar Koppel, Peeter Saari. Eesti Teaduste Akadeemia. Lk 81.
Kirjandus[muuda | muuda lähteteksti]
- David Halliday, Robert Resnick, Jearl Walker. Füüsika põhikursus. Teine köide. Eesti Füüsika Selts, 2008, ISBN 978-9985-9078-9-4
- Rein-Karl Loide. Sissejuhatus kvantmehaanikasse. Avita, 2007, ISBN 978-9985-2-1282-0
- Taylor, J., Modern Physics for Scientists and Engineers, Prentice Hall, 2004, ISBN 978-0138057152
- Chaudry, A., Fundamentals of Nanoscaled Field Effect Transistors, Springer, 2013, ISBN 978-1-4614-6821-9
- Ilmar Koppel, Peeter Saari. Teadusmõte Eestis. Täppisteadused. Eesti Teaduste Akadeemia. Lk 81. ISBN 9985-50-389-9


