Konjunktsioon: erinevus redaktsioonide vahel
PResümee puudub |
P pisitoimetamine |
||
| 2. rida: | 2. rida: | ||
'''Konjunktsioon''' ehk '''loogiline korrutamine''' ehk '''"ning"''' on üks [[binaarne tehe|binaarne]] [[loogikatehe]] [[lauseloogika]]t sisaldavates [[sümbolloogika]] süsteemides. |
'''Konjunktsioon''' ehk '''loogiline korrutamine''' ehk '''"ning"''' on üks [[binaarne tehe|binaarne]] [[loogikatehe]] [[lauseloogika]]t sisaldavates [[sümbolloogika]] süsteemides. |
||
[[ |
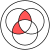
[[Pilt:Venn0001.svg|pisi|<math>\scriptstyle A \and B</math> tähisav [[Venn diagram|Venni diagramm]]]] |
||
[[ |
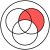
[[Pilt:Venn 0000 0001.svg|pisi|<math>\scriptstyle A \and B \and C</math> tähistav Venni diagramm]] |
||
Konjunktsioon ehk loogiline korrutamine on binaarne loogikatehe: lausete ''A'' ja ''B'' konjunktsioon ''A''<math>\and</math>''B'' loetakse tõeseks parajasti siis, kui laused ''A'' ja ''B'' on mõlemad tõesed ning vääraks kõigil muudel juhtudel.<ref name=":1" /> |
Konjunktsioon ehk loogiline korrutamine on binaarne loogikatehe: lausete ''A'' ja ''B'' konjunktsioon ''A''<math>\and</math>''B'' loetakse tõeseks parajasti siis, kui laused ''A'' ja ''B'' on mõlemad tõesed ning vääraks kõigil muudel juhtudel.<ref name=":1" /> |
||
"A ja B" on tõene siis ja ainult siis, kui A on tõene ja B on tõene. |
"A ja B" on tõene siis ja ainult siis, kui A on tõene ja B on tõene. |
||
Seotud mõisted teistes valdkondades on järgmised: |
Seotud mõisted teistes valdkondades on järgmised: |
||
* [[Loomulik keel|loomulikus keeles]] on konjunktsiooniga kõige sarnasem sõna "ja" või "ning";<ref name=":1" /> |
* [[Loomulik keel|loomulikus keeles]] on konjunktsiooniga kõige sarnasem sõna "ja" või "ning";<ref name=":1" /> |
||
* [[ |
* [[hulgateooria]]s – [[ühisosa]]; |
||
* [[ |
* [[predikaatloogika]]s – [[üldisuskvantor]]. |
||
Konjunktsiooni ja [[ |
Konjunktsiooni ja [[eitus]]e abil on võimalik esitada kõik ülejäänud loogikatehted.<ref name="JGk4o" /> |
||
==Notatsioon== |
==Notatsioon== |
||
| 30. rida: | 30. rida: | ||
===Tõeväärtustabel=== |
===Tõeväärtustabel=== |
||
[[ |
[[Pilt:Multigrade operator AND.svg|pisi|Vasakul poolel olevate argumentide konjunktsioonid – [[Sierpinski kolmnurk|Sierpinski kolmnurga]] tõesed [[Bitt|bitid]]]] |
||
Valemi<math>~A \and B</math> tõeväärtustabel:<ref name="6iPPD" /> |
Valemi<math>~A \and B</math> tõeväärtustabel:<ref name="6iPPD" /> |
||
| 63. rida: | 63. rida: | ||
|<math>B \and A</math> |
|<math>B \and A</math> |
||
|- |
|- |
||
|[[ |
|[[Pilt:Venn0001.svg|50px]] |
||
| <math>\Leftrightarrow</math> |
| <math>\Leftrightarrow</math> |
||
|[[ |
|[[Pilt:Venn0001.svg|50px]] |
||
|} |
|} |
||
| 81. rida: | 81. rida: | ||
|<math>~C</math> |
|<math>~C</math> |
||
|- |
|- |
||
|[[ |
|[[Pilt:Venn 0101 0101.svg|50px]] |
||
|<math>~~~\and~~~</math> |
|<math>~~~\and~~~</math> |
||
|[[ |
|[[Pilt:Venn 0000 0011.svg|50px]] |
||
| <math>\Leftrightarrow</math> |
| <math>\Leftrightarrow</math> |
||
|[[ |
|[[Pilt:Venn 0000 0001.svg|50px]] |
||
| <math>\Leftrightarrow</math> |
| <math>\Leftrightarrow</math> |
||
|[[ |
|[[Pilt:Venn 0001 0001.svg|50px]] |
||
|<math>~~~\and~~~</math> |
|<math>~~~\and~~~</math> |
||
|[[ |
|[[Pilt:Venn 0000 1111.svg|50px]] |
||
|} |
|} |
||
| 106. rida: | 106. rida: | ||
|- |
|- |
||
|- |
|- |
||
|[[ |
|[[Pilt:Venn 0101 0101.svg|50px]] |
||
|<math>\and</math> |
|<math>\and</math> |
||
|[[ |
|[[Pilt:Venn 0011 1111.svg|50px]] |
||
| <math>\Leftrightarrow</math> |
| <math>\Leftrightarrow</math> |
||
|[[ |
|[[Pilt:Venn 0001 0101.svg|50px]] |
||
| <math>\Leftrightarrow</math> |
| <math>\Leftrightarrow</math> |
||
|[[ |
|[[Pilt:Venn 0001 0001.svg|50px]] |
||
|<math>\or</math> |
|<math>\or</math> |
||
|[[ |
|[[Pilt:Venn 0000 0101.svg|50px]] |
||
|} |
|} |
||
| 135. rida: | 135. rida: | ||
|- |
|- |
||
|- |
|- |
||
|[[ |
|[[Pilt:Venn 0101 0101.svg|50px]] |
||
|<math>\and</math> |
|<math>\and</math> |
||
|[[ |
|[[Pilt:Venn 0011 1100.svg|50px]] |
||
| <math>\Leftrightarrow</math> |
| <math>\Leftrightarrow</math> |
||
|[[ |
|[[Pilt:Venn 0001 0100.svg|50px]] |
||
| <math>\Leftrightarrow</math> |
| <math>\Leftrightarrow</math> |
||
|[[ |
|[[Pilt:Venn 0001 0001.svg|50px]] |
||
|<math>\oplus</math> |
|<math>\oplus</math> |
||
|[[ |
|[[Pilt:Venn 0000 0101.svg|50px]] |
||
|} |
|} |
||
| 160. rida: | 160. rida: | ||
|- |
|- |
||
|- |
|- |
||
|[[ |
|[[Pilt:Venn 0101 0101.svg|50px]] |
||
|<math>\and</math> |
|<math>\and</math> |
||
|[[ |
|[[Pilt:Venn 0011 0000.svg|50px]] |
||
| <math>\Leftrightarrow</math> |
| <math>\Leftrightarrow</math> |
||
|[[ |
|[[Pilt:Venn 0001 0000.svg|50px]] |
||
| <math>\Leftrightarrow</math> |
| <math>\Leftrightarrow</math> |
||
|[[ |
|[[Pilt:Venn 0001 0001.svg|50px]] |
||
|<math>\nrightarrow</math> |
|<math>\nrightarrow</math> |
||
|[[ |
|[[Pilt:Venn 0000 0101.svg|50px]] |
||
|} |
|} |
||
| 185. rida: | 185. rida: | ||
|- |
|- |
||
|- |
|- |
||
|[[ |
|[[Pilt:Venn 0101 0101.svg|50px]] |
||
|<math>\and</math> |
|<math>\and</math> |
||
|[[ |
|[[Pilt:Venn 0000 0011.svg|50px]] |
||
| <math>\Leftrightarrow</math> |
| <math>\Leftrightarrow</math> |
||
|[[ |
|[[Pilt:Venn 0000 0001.svg|50px]] |
||
| <math>\Leftrightarrow</math> |
| <math>\Leftrightarrow</math> |
||
|[[ |
|[[Pilt:Venn 0001 0001.svg|50px]] |
||
|<math>\and</math> |
|<math>\and</math> |
||
|[[ |
|[[Pilt:Venn 0000 0101.svg|50px]] |
||
|} |
|} |
||
|} |
|} |
||
| 206. rida: | 206. rida: | ||
|<math>A~</math> |
|<math>A~</math> |
||
|- |
|- |
||
|[[ |
|[[Pilt:Venn01.svg|36px]] |
||
|<math>~\and~</math> |
|<math>~\and~</math> |
||
|[[ |
|[[Pilt:Venn01.svg|36px]] |
||
| <math>\Leftrightarrow</math> |
| <math>\Leftrightarrow</math> |
||
|[[ |
|[[Pilt:Venn01.svg|36px]] |
||
|} |
|} |
||
| 223. rida: | 223. rida: | ||
|<math>(B \and C)</math> |
|<math>(B \and C)</math> |
||
|- |
|- |
||
||[[ |
||[[Pilt:Venn 1011 1011.svg|50px]] |
||
| <math>\Rightarrow</math> |
| <math>\Rightarrow</math> |
||
||[[ |
||[[Pilt:Venn 1111 1011.svg|50px]] |
||
| <math>\Leftrightarrow</math> |
| <math>\Leftrightarrow</math> |
||
||[[ |
||[[Pilt:Venn 0000 0101.svg|50px]] |
||
|<math>\rightarrow</math> |
|<math>\rightarrow</math> |
||
||[[ |
||[[Pilt:Venn 0000 0011.svg|50px]] |
||
|} |
|} |
||
| 240. rida: | 240. rida: | ||
|<math>A \and B</math> |
|<math>A \and B</math> |
||
|- |
|- |
||
|[[ |
|[[Pilt:Venn0001.svg|50px]] |
||
| <math>\Rightarrow</math> |
| <math>\Rightarrow</math> |
||
|[[ |
|[[Pilt:Venn0001.svg|60px]] |
||
|- |
|- |
||
| |
| |
||
| 257. rida: | 257. rida: | ||
|<math>A \or B</math> |
|<math>A \or B</math> |
||
|- |
|- |
||
|[[ |
|[[Pilt:Venn0001.svg|60px]] |
||
| <math>\Rightarrow</math> |
| <math>\Rightarrow</math> |
||
|[[ |
|[[Pilt:Venn0111.svg|50px]] |
||
|- |
|- |
||
|{{small|(vajab testimist)}} |
|{{small|(vajab testimist)}} |
||
| 273. rida: | 273. rida: | ||
==Rakendusi informaatikas== |
==Rakendusi informaatikas== |
||
[[ |
[[Pilt:AND Gate diagram.svg|pisi|AND [[loogikavärav]]]] |
||
Kõrgetasemelises programmeerimises ja digitaalses elektroonikas on konjunktsioon tavaliselt tähistatud infiks operaatoriga, enamasti tähisega nagu "<code>AND</code>", algebraline korrutamistehe või sümbol "<code>&</code>". |
Kõrgetasemelises programmeerimises ja digitaalses elektroonikas on konjunktsioon tavaliselt tähistatud infiks operaatoriga, enamasti tähisega nagu "<code>AND</code>", algebraline korrutamistehe või sümbol "<code>&</code>". |
||
| 283. rida: | 283. rida: | ||
* <code>1 AND 1</code> = <code>1</code>. |
* <code>1 AND 1</code> = <code>1</code>. |
||
Seda operatsiooni saab rakendada ja kahele binaarsele sõnale, mida vaadeldakse võrdse pikkusega [[ |
Seda operatsiooni saab rakendada ja kahele binaarsele sõnale, mida vaadeldakse võrdse pikkusega [[bitistring]]idena, leides iga samal positsioonil oleva bitipaari jaoks neile vastava AND väärtuse. Näiteks; |
||
* <code>11000110 AND 10100011</code> = <code>10000010</code>. |
* <code>11000110 AND 10100011</code> = <code>10000010</code>. |
||
Seda saab kasutada, et valida mingi osa bitistringist [[ |
Seda saab kasutada, et valida mingi osa bitistringist [[bitimask]]i kasutades. Näiteks <code>1001'''1'''101 AND 0000'''1'''000</code> = <code>0000'''1'''000</code>eraldab viienda biti 8-bitisest bitistringist. |
||
[[Arvutivõrk |
[[Arvutivõrk]]ude teaduses, kasutatakse bitimaske olemasoleva alamvõrgu võrguaadressi leidmisel nii, et ANDitakse IP aadress ja alamvõrgu mask. |
||
Loogiline konjunktsioon "<code>AND</code>" on ka kasutusel [[SQL]] operatsioonides [[ |
Loogiline konjunktsioon "<code>AND</code>" on ka kasutusel [[SQL]] operatsioonides [[andmebaas]]i päringutel. |
||
==Vastavus hulgateoorias== |
==Vastavus hulgateoorias== |
||
Elemendi kuuluvus kahe hulga [[ |
Elemendi kuuluvus kahe hulga [[ühisosa]]sse on [[hulgateooria]]s defineeritud loogilise konjunktsiooni abil: ''x'' ∈ ''A'' ∩ ''B'' [[Parajasti siis, kui|siis ja ainult siis, kui]] (''x'' ∈ ''A'') ∧ (''x'' ∈ ''B''). Selle vastavuse tõttu jagab hulgateoreetiline ühisosa samuti mitmeid loogilise konjunktsiooni omadusi, nagu [[assotsiatiivsus]], [[kommutatiivsus]] ja [[idempotentsus]]. |
||
==Loomulik keel== |
==Loomulik keel== |
||
| 309. rida: | 309. rida: | ||
{{viited|allikad= |
{{viited|allikad= |
||
<ref name=":1">{{Raamatuviide|autor=Enn Kasak|pealkiri=Loogika alused|aasta=|koht=|kirjastus=|lehekülg=261}}</ref> |
<ref name=":1">{{Raamatuviide|autor=Enn Kasak|pealkiri=Loogika alused|aasta=|koht=|kirjastus=|lehekülg=261}}</ref> |
||
| ⚫ | |||
<ref name="JGk4o">{{Netiviide|Autor=Valdis Laan|URL=https://courses.ms.ut.ee/LTMS.00.019/2018_spring/uploads/Main/kon.pdf|Pealkiri=Diskreetne Matemaatika I. Kevad 2018. Loengukonspekt.|Väljaanne=|Aeg=|Kasutatud=|Täpsustus=Teoreem 1.24}}</ref> |
<ref name="JGk4o">{{Netiviide|Autor=Valdis Laan|URL=https://courses.ms.ut.ee/LTMS.00.019/2018_spring/uploads/Main/kon.pdf|Pealkiri=Diskreetne Matemaatika I. Kevad 2018. Loengukonspekt.|Väljaanne=|Aeg=|Kasutatud=|Täpsustus=Teoreem 1.24}}</ref> |
||
| ⚫ | |||
<ref name="6iPPD">{{Raamatuviide|autor=Tõnu Tamme, Tanel Tammet, Rein Prank|pealkiri=Loogika: Mõtlemisest tõestamiseni|aasta=|koht=|kirjastus=|lehekülg=69}}</ref> |
<ref name="6iPPD">{{Raamatuviide|autor=Tõnu Tamme, Tanel Tammet, Rein Prank|pealkiri=Loogika: Mõtlemisest tõestamiseni|aasta=|koht=|kirjastus=|lehekülg=69}}</ref> |
||
<ref name="mmC5R">{{Cite web|last=Smith|first=Peter|url=http://www.logicmatters.net/resources/pdfs/ProofSystems.pdf|title=Types of proof system|page=4}}</ref> |
<ref name="mmC5R">{{Cite web|last=Smith|first=Peter|url=http://www.logicmatters.net/resources/pdfs/ProofSystems.pdf|title=Types of proof system|page=4}}</ref> |
||
| 320. rida: | 320. rida: | ||
{{Loogiline tehe}} |
{{Loogiline tehe}} |
||
[[Kategooria:Loogika]] |
[[Kategooria:Loogika]] |
||
[[Kategooria:Automaatika]] |
[[Kategooria:Automaatika]] |
||
Redaktsioon: 1. mai 2019, kell 15:15
| See artikkel räägib loogikatehtest, astronoomia mõiste kohta vaata artiklit Konjunktsioon (astronoomia), keeleteaduse mõiste kohta vaata artiklit sidesõna. |
Konjunktsioon ehk loogiline korrutamine ehk "ning" on üks binaarne loogikatehe lauseloogikat sisaldavates sümbolloogika süsteemides.


Konjunktsioon ehk loogiline korrutamine on binaarne loogikatehe: lausete A ja B konjunktsioon AB loetakse tõeseks parajasti siis, kui laused A ja B on mõlemad tõesed ning vääraks kõigil muudel juhtudel.[1]
"A ja B" on tõene siis ja ainult siis, kui A on tõene ja B on tõene.
Seotud mõisted teistes valdkondades on järgmised:
- loomulikus keeles on konjunktsiooniga kõige sarnasem sõna "ja" või "ning";[1]
- hulgateoorias – ühisosa;
- predikaatloogikas – üldisuskvantor.
Konjunktsiooni ja eituse abil on võimalik esitada kõik ülejäänud loogikatehted.[2]
Notatsioon
Konjunktsiooni tähistatakse tavaliselt infiks-operaatoriga:
- matemaatikas ja loogikas kasutatakse sümbolit või või
- elektroonikas kasutatakse sümbolit
- programmeerimiskeeltes kasutatakse tähistust
&,&&, võiand - Jan Łukasiewiczi loogika prefiksnotatsioonis on vastav operaator K, mis tuleb poolakeelsest sõnast koniunkcja[3] (eesti keeles: konjunktsioon).
Definitsioon
Loogiline konjunktsioon on operatsioon kahel loogilisel väärtusel, enamasti kahel propositsioonil, mis väljastab väärtuse tõene siis ja ainult siis, kui mõlemad operandid on tõesed.
Tõeväärtustabel

Valemi tõeväärtustabel:[4]
| SISEND | VÄLJUND | |
| TÕENE | TÕENE | TÕENE |
| TÕENE | VÄÄR | VÄÄR |
| VÄÄR | TÕENE | VÄÄR |
| VÄÄR | VÄÄR | VÄÄR |
Teiste operaatorite läbi defineerimine
Süsteemides, kus lauseloogika konnektor pole primitiiv, võib konjunktsiooni defineerida järgmiselt:[5]
Omadused
Konjunktsioonil on järgnevad omadused:
kommutatiivsus: jah
assotsiatiivsus: jah

|

|

|

|

|
distributiivsus: mitmete loogikatehetega jah, näiteks tehtega või, kuid mitte kõigiga

|
|

|

|

|
| Näiteid konjunktsiooni distributiivsusest teiste tehetega | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
välistava võiga: jah
materiaalse mitteimplikatsiooniga: jah
iseendaga: jah
|
idempotentsus: jah
monotoonsus: jah

|

|

|

|
tõesust säilitav: jah
Kui kõik sisendid on tõesed, on ka väljund tõene
| (vajab testimist) |
väärsust säilitav: jah
Kui kõik sisendid on väärad, on ka väljund väär.
| (vajab testimist) |
Walshi spekter: (1,-1,-1,1)
Mittelineaarsus: 1 (funktsioon on kõver)
Kasutades binaarseid väärtuseid tõese (1) ja väära (0) jaoks, siis töötab loogiline konjuktsioon täpselt nagu aritmeetiline korrutamine.
Rakendusi informaatikas

Kõrgetasemelises programmeerimises ja digitaalses elektroonikas on konjunktsioon tavaliselt tähistatud infiks operaatoriga, enamasti tähisega nagu "AND", algebraline korrutamistehe või sümbol "&".
Loogilist konjunktsiooni kasutatakse tihti bitikaupa tehtavates operatsioonides, kus tähistab 0 väära ja 1 on tõene.
0 AND 0=0,0 AND 1=0,1 AND 0=0,1 AND 1=1.
Seda operatsiooni saab rakendada ja kahele binaarsele sõnale, mida vaadeldakse võrdse pikkusega bitistringidena, leides iga samal positsioonil oleva bitipaari jaoks neile vastava AND väärtuse. Näiteks;
11000110 AND 10100011=10000010.
Seda saab kasutada, et valida mingi osa bitistringist bitimaski kasutades. Näiteks 10011101 AND 00001000 = 00001000eraldab viienda biti 8-bitisest bitistringist.
Arvutivõrkude teaduses, kasutatakse bitimaske olemasoleva alamvõrgu võrguaadressi leidmisel nii, et ANDitakse IP aadress ja alamvõrgu mask.
Loogiline konjunktsioon "AND" on ka kasutusel SQL operatsioonides andmebaasi päringutel.
Vastavus hulgateoorias
Elemendi kuuluvus kahe hulga ühisosasse on hulgateoorias defineeritud loogilise konjunktsiooni abil: x ∈ A ∩ B siis ja ainult siis, kui (x ∈ A) ∧ (x ∈ B). Selle vastavuse tõttu jagab hulgateoreetiline ühisosa samuti mitmeid loogilise konjunktsiooni omadusi, nagu assotsiatiivsus, kommutatiivsus ja idempotentsus.
Loomulik keel
Nagu ka matemaatilise loogika teiste tehetega, on loogiline konjunktsioon ning seotud, kuid mitte täpselt võrdne, grammatilisele konjunktsioonile ning loomulikus keeles.
Eesti keele sõnal "ning" (või "ja") on omadused, mida loogiline konjunktsioon ei säilita. Näiteks tähistab "ning" vahel järjekorda. Lause "Nad abiellusid ning said lapse" tähendaks tavaarusaama järgi, et abiellumine toimus enne lapse saamist. Sõna "ning" ("ja") võib ka võib ka väljendada mingi asja osadeks tegemist, nagu lauses "Eesti lipp on sinine, must ja valge". See lause ei tähenda, et Eesti lipp on samaaegselt sinine, must ja valge, vaid seda, et lipu erinevatel osadel on erinev värv.
Vaata ka
Viited
- ↑ 1,0 1,1 Enn Kasak. Loogika alused. Lk 261.
- ↑ Valdis Laan. "Diskreetne Matemaatika I. Kevad 2018. Loengukonspekt" (PDF). Teoreem 1.24.
- ↑ Józef Maria Bocheński (1959), A Précis of Mathematical Logic, translated by Otto Bird from the French and German editions, Dordrecht, North Holland: D. Reidel, passim.
- ↑ Tõnu Tamme, Tanel Tammet, Rein Prank. Loogika: Mõtlemisest tõestamiseni. Lk 69.
{{raamatuviide}}: CS1 hooldus: mitu nime: autorite loend (link) - ↑ Smith, Peter. "Types of proof system" (PDF). Lk 4.