Allika ja koormuse sobitamine

Allika ja koormuse sobitamine tähendab elektroonikas ahelate moodustamist nii, et koormuse sisendimpedants oleks väärtusega, mis tagaks maksimaalse võimsuse ülekande allikalt koormusele. Selleks peavad koormuse ja allika impedantside reaalosad olema võrdsed ja imaginaarosad vastandmärgiga ehk teineteist kompenseerima.

Matemaatiliselt öeldakse, et allika impedants peab võrduma koormuse impedantsi kaaskompleksarvuga:

Z_{\text{allikas}}={\overline {Z_{\text{koormus}}}}

ehk

R_{\text{allikas}}+jX_{\text{allikas}}=R_{\text{koormus}}-jX_{\text{koormus}}.

Sobitamine on algselt välja arendatud elektriahelate tarbeks, kuid hiljem on leitud adaptatsioone ka teistes valdkondades. Sobitamisega peab arvestama alati, kui omavahel on ühendatud kaks suvalist järjestikust raadiosageduslikku ahelat: ostsillaator – modulaator; modulaator – eelvõimendi; võimsusvõimendi ‒ antenn jne.

Sobitamine[muuda | muuda lähteteksti]

Antud teema olulisus avaldub eelkõige raadiosageduslike süsteemide ekspluateerimisel ja projekteerimisel. Raadiosaatjates täidab allika ülesannet tavaliselt raadiosaatja lõppaste (võimsusvõimendi) ja koormuseks on tavaolukorras antenn. Energia ülekandeks on levinud süsteem: saatja – ülekandeliin – antenn. Vahetades saatja vastuvõtja vastu saame süsteemi, millega on võimalik püüda elektromagnetlaineid keskkonnast. Mõlemale süsteemile esitatakse professionaalsetes süsteemides samu nõudeid. Peamiselt vajame maksimaalset energiaülekannet. Seni kuni on tegemist raadiosagedustega, peab alati mõtlema ka elektroonikaseadme astmete omavahelise sobituse peale. Sobitamisest rääkides mõeldakse näivtakistuste Z sobitamist. E süsteemis toimuks maksimaalne võimsuse ülekanne, vastavalt maksimaalse võimsuse ülekande teoreemile^[1] plokist A plokki B , peavad A väljundimpedantsi ja B sisendimpedantsi reaalosad olema võrdsed ja imaginaarosad vastasmärgiga. Alati ei ole sobituse saamine kuigi lihtne, sest enamikul juhtudel sõltub ahela impedants kasutatavast sagedusest ja on kompleksne, s.t sisaldab imaginaarosa.

Maksimaalse võimsusülekande teoreem[muuda | muuda lähteteksti]

Selleks et saada maksimaalset võimsust allikalt, millel takistus on puhtaktiivne, peab aktiivtakistusliku koormuse takistus olema võrdne allika klemmidel nähtava sisetakistusega. Sealjuures on saadav kasutegur η = 0,5. Raadiosageduslike süsteeme omavahel sobitades lähtutakse just sellest printsiibist.

Võimendite A ja B sobitamise näide[muuda | muuda lähteteksti]

Võimendi A väljundtakistus on induktiivse iseloomuga. Et seda induktiivset reaktiivtakistust kompenseerida, peab võimendi B sisendtakistuse reaktiivosa arvuline väärtus olema sama, aga vastandmärgiga, ehk mahtuvuslik. Sellisel juhul leiab ahelas aset resonants, mille korral reaktiivsuste mõju taandub süsteemist välja:

Z_{\text{allikas}}={Z_{\text{koormus}}}=R_{\text{allikas}}+jX_{L};

Z_{\text{koormus}}={R_{\text{koormus}}}+jX_{C}.

Sarnaselt võib ette kujutada ka antenni sobitust võimendiga, kus takistused peavad olema võrdsed. Tegelikult on selline olukord saavutatav vaid ühel kindlal sagedusel, sest lainetakistus (laineimpedants) sõltub kasutatavast sagedusest.

Näiteks poollainedipooli korral on Z₀ = 73+j42,5; kui aga dipooli pikkust õige pisut vähendada (või sagedust suurendada) väärtuseni 0,485λ, siis Z₀ = 73+j0 ja on seega puhtaktiivne. See on üks põhjustest, miks koaksiaalkaabli lainetakistus on enamasti 75 Ω.

Allika ja koormuse omavahelise sobituse tagamiseks ühendatakse nende vahele vastav ahel või komponent, mille valik sõltub allika ja koormuse omadustest.

Sobitusviisid[muuda | muuda lähteteksti]

Sobituse meetodeid on mitmesuguseid, järgnevalt on toodud vaid mõned võimalused.

Trafosidestus[muuda | muuda lähteteksti]

Trafosidestus ^[2] on kohane madalsageduslikes süsteemides, kui on vaja sobitada aktiivtakistusi. Näiteks muundada helisagedusliku lampvõimendi kõrge väljundtakistus palju väiksema sisendtakistusega valjuhääldi sisetakistuseks. Iga koormuse impedants, mis on ühendatud ideaalse trafo sekundaarmähisele, põhjustab kadudeta võimsuse ülekande primaarmähiselt. Seega kehtib seos $I_{N2}\times U_{N2}=I_{N1}\times U_{N1}$ .

Kasutades ideaalse trafo pinge ja voolu ülekande valemeid

{U_{2} \over U_{1}}={N_{2} \over N_{1}}={I_{1} \over I_{2}},

U_{2}={N_{2}\times U_{1} \over N_{1}},

I_{2}={N_{1}\times I_{1} \over N_{2}}

ning arvestades, et

Z_{\text{allikas}}={U_{2} \over I_{2}}

ja

Z_{\text{koormus}}={U_{2} \over I_{1}},

saame:

Z_{\text{allikas}}={{N_{2}\times N_{2}\times U_{1}} \over {N_{1}\times N_{1}\times I_{1}}}=\left({N_{2} \over N_{1}}\right)^{2}\times Z_{\text{koormus}}.

Eelnevast tulenevalt on vajalik keerdude suhe järgmine:

{N_{1} \over N_{2}}={\sqrt {Z_{\text{koormus}} \over Z_{\text{allikas}}}}.

Induktiivne sidestus[muuda | muuda lähteteksti]

Aktiivkoormus[muuda | muuda lähteteksti]

Induktiivselt sidestatud sobitusahelad on näha joonistel A ja B , kus R1 on koormuse takistus, kuhu energia on tarvis saata, R2 – takistus, mida "näeb" allikas. L1 ja C1 on komponendid, mille abil häälestatakse ahel sobilikule sagedusele. Vajaduse korral on L1 ja L2 vaheline sidestus muudetav. Ahel C1-L1-L2 moodustab impedantsi transformaatori, mille impedants on muudetav laias vahemikus. Takistus R2, mis on sidestatud üle L1, sõltub ahela L1-C1-R1 hüvetegurist Q, poolidevahelisest sidestustegurist k ja pooli L2 reaktiivtakistusest. Ligilähedaselt võib öelda, et kehtib seos

R_{2}={k}^{2}X_{L2}Q,

kus $X_{L2}$ on $L_{2}$ reaktiivtakistus töösagedusel. Seega soovitud R2 väärtuse saavutamiseks võib muuta poolidevahelist sidestust või muuta ahela hüvetegurit Q, mis on paljudel juhtudel ka ainus võimalus. Ahela Q sõltub valitud lahendusest A või B.

Kasutades rööpvõnkeringi skeemi A, saame

Q_{\text{roop}}={R_{1} \over X_{C1}}.

Skeem A sobib juhul, kui R1>R2.

Kasutades jadavõnkeringi skeemi B, saame:

Q_{\text{jada}}={X_{C1} \over R_{1}}.

Skeem B sobib juhul, kui R1<R2 või samas suurusjärgus kui R2.

Reaktiivkoormus[muuda | muuda lähteteksti]

Enamasti ei ole koormuseks aktiivtakistus, vaid näivtakistus. Näivtakistuse reaktiivtakistuslikku osa on alati võimalik kujutada aktiivosaga rööbiti või jadamisi oleva mahtuvusliku või induktiivse komponendina. Võttes arvesse reaktiivosast tekkiva L1 või C1 muutuse, saame kasutada samu valemeid nagu aktiivkoormuse puhulgi. Tekkivate uute mahtuvuste ja induktiivsuste arvutamiseks saab kasutada elektrotehnikast tuntud valemeid. Näiteks kui lisandub rööbiti olev mahtuvus (joonis C), siis kogumahtuvus on $C_{1}+C$ , või kui lisandub jadamahtuvus (joonis D), siis kogumahtuvus on $C_{\text{kogu}}={1 \over ({1 \over C_{1}}+{1 \over C_{1}})}.$

Sisendreaktiivsuse kompenseerimine[muuda | muuda lähteteksti]

Vaadeldes eelmisi skeeme, kui koormuse reaktiivtakistus on mahtuvuslik ja seda on võimalik kompenseerida $C_{1}$ muutmisega, siis ahela hüvetegur $Q$ ei muutu. Kui aga koormuse reaktiivtakistus on induktiivne, siis sobiliku $Q$ säilitamiseks oleks tarvis muuta $L_{1}$ induktiivsust, kuid see ei ole alati võimalik. Seetõttu võib olla tarvilik koormuse reaktiivsust kompenseerida. Selleks lisatakse koormusele väline reaktiivsus, mille arvuline suurus on võrdne koormuse reaktiivsusega, kuid vastandmärgiga. Lisades mahtuvusliku iseloomuga koormusele $RC$ rööbiti induktiivsuse $L$ (joonis E), moodustub resonantssagedusel rööpvõnkering ja sisuliselt muutub kogu koormus puhtaktiivseks $R_{1}$ . Joonisel F lisatakse mahtuvuslikule koormusele jadamisi induktiivsus $L$ ja resonantssagedusel käitub ahel jadavõnkeringina, resulteerides puht-takistusliku koormusena R1.

L-sobitusahel[muuda | muuda lähteteksti]

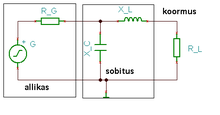
Selline ahel on üks lihtsamini teostatavaid sobitusi. Peamiseks piiravaks teguriks on antud lülil sagedusriba muutumine. L-ahela kaks levinumat versiooni on toodud joonistel G ja H; neil on võime summutada mürasid ja kõrgemaid harmoonilisi.

Joonisel G oleva ahela komponendid saab arvutada järgmiste valemitega: