Loogikavärav
See artikkel on esitatud liitmiseks artikliga Loogikavärav (bioloogia). Lisateavet artikli arutelust |
Loogikavärav (ingl logic gate) ehk loogikaelement on digitaalne elektroonikalülitus, mis sooritab Boole'i algebra operatsioone. Sellel on üks väljund ja vähemalt üks sisend, kus igaühes on üks kahest binaarväärtusest (0 või 1). Kõrget (1) ja madalat (0) olekut eristatakse nende erineva pinge järgi. Esimestes loogikalülitustes, kui toitepinge oli 5 V, jäi kõrge pingenivoo vahemikku 2,5‒5 V ja madal nivoo vahemikku 0‒0,4 V. Tänapäeva lülitustes on toitepinge 1 V ringis. L
Kuigi enamik loogikaväravaid on elektroonilised ning kasutavad transistore, ei pea need ilmtingimata töötama elektrivoolu toimel, vaid nad võivad põhineda ka vedelikel, suruõhul (Sortebergi relee), optikal või mehaanikal. Loogikaväravaid on tehtud ka DNA-st (bioloogiline arvuti MAYA).
Tänapäevased elektroonilised loogikaväravad[muuda | muuda lähteteksti]
Erinevad tehnoloogiad[muuda | muuda lähteteksti]
Kõige lihtsam elektrooniline loogikavärav on võimalik ehitada kasutades dioode ja takisteid. Nii on võimalik luua AND- ja OR-väravaid, aga mitte pöördväravaid (NAND või NOR), seega ei saa niimoodi luua kõiki Boole'i algebra operatsioone. Lisaks on veel dioodloogika miinuseks tema "hägune" tulemus, ehk 0 pole päris 0 ja 1 pole päris 1. Seetõttu ei saa luua keerulisemaid skeeme, kus järgnevad mitmed diood-loogikaväravad üksteise järel ilma mingisugust signaali võimendavat seadet kasutamata.
Takisti-transistor-väravatega kadus dioodväravate suur miinus. Nüüd oli võimalik luua nii pikki skeeme, kui oli vaja, kasutamata eraldi signaali võimendeid. Kombineerides erinevaid takisti-transistor-väravaid saab läbi viia kõiki Boole’i algebra operatsioone. Peatselt leiti, et üks transistor suudab töö kiiremini valmis saada kui kaks dioodi. Sündis transistor-transistor loogikaskeem, mis oli oma eelkäijatest kiirem ja võttis märgatavalt vähem ruumi, tehes loogikaskeemid väiksemaks ja efektiivsemaks. Tänapäeval on praktiliselt täielikult tavalise bipolaartransistori asendanud väljatransistorid (FET), täpsemalt isoleeritud paisuga väljatransistorid (metall-oksiid-pooljuht väljatransistor, inglise keeles MOSFET), mida kasutatakse komplementaarete paaridena (CMOS).
Tänapäev[muuda | muuda lähteteksti]
Väikesemõõduliste loogikaskeemide jaoks kasutavad disainerid tänapäeval eeltoodetud standardseid loogikaväravaid. Üha enam on hakatud kasutama programmeeritavaid loogikaseadmeid, mis võimaldavad kiibil suurt elementide pakkimistihedust. Programmeeritavad loogikaseadmed nagu FPGA lubavad muuta komponentide programmeerimise teel kiipide funktsioone. Elektroonilistes loogikaskeemides töötavad transistorid lülitirežiimis, kus nende ümberlülitamiseks kulub väga vähe voolu.
Loogikaseadmed[muuda | muuda lähteteksti]
Loogikaväravatest koostatakse sellised seadmed nagu multipleksorid, registrid, aritmeetika-loogikaplokid (ALU), arvutimälud, kuni keeruliste mikroprotsessoriteni välja, mis võivad sisaldada mitusada miljonit loogikaväravat (NAND koosneb neljast transistorist).
Boole'i algebra funktsioonid[muuda | muuda lähteteksti]
Kokku on 16 Boole'i algebra funktsiooni, milles on defineeritud kaks kommutatiivset, assotsiatiivset, teineteise suhtes distributiivset ja neelduvat binaarset tehet (konjunktsioon ning disjunktsioon) ja involutsioon (eitus). Need 16 funktsiooni on koos kõigi võimalike väljunditega järgmises tabelis.
Neli noolega funktsiooni on implikatsioonid.
Tingmärgid[muuda | muuda lähteteksti]
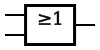
Elektriskeemidel kujutatakse loogikaväravaid kahte liiki tingmärkidega (sümbolitega). Kõige laiemalt on kasutusel USA standardi ANSI 91-1984 kohased tingmärgid. Euroopa riikides kasutatakse standardiga IEC 60617-12 : 1997 kehtestatud ristkülikukujulisi tingmärke.
Ristkülikukujulistel sümbolitel on iga erineva värava jaoks olemas oma sümbol ja seetõttu saab nendega kujutada palju rohkemaid skeeme kui USA sümbolitega. Ristkülikuliste sümbolite loomise ajendiks oli ühtne meetod keeruliste loogikasüsteemide jooniste tegemiseks. Standard IEC 617-12 ja tema järeltulija IEC 60617-2 ei sisalda enam ANSI sümboleid, küll aga on need veel alles ANSI/IEEE 91 ja 91a standardites.
| Tüüp | USA ANSI 91-1984 | IEC 617-12 |
|---|---|---|
| AND | 
|

|
| XOR | 
|

|
| OR | 
|
|
| NOR | 
|

|
| XNOR | 
|

|
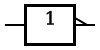
| NOT | 
|
|
| NAND | 
|

|
Elektroonikas nimetatakse NOT-väravat inverteriks. ANSI järgi märgitakse NOT-operatsiooni pisikese ringiga ning ristkülikulise kuju puhul lisatakse väljundisse väike kaldkriips.
Charles Sanders Peirce[muuda | muuda lähteteksti]
Charles Sanders Peirce (1880) näitas, et NAND-väravaid (alternatiiviks NOR-värav) kombineerides on võimalik teostada ka kõik muud loogilised väravad, aga tema sellekohast tööd ei avaldatud enne aastat 1935. Aastal 1913 avaldas Henry M. Sheffer esimese tõendi selle kohta.
Veel kaks väravat on "välistav või" ehk XOR-funktsioon ja tema pöördvärav "välistav NOR" ehk XNOR. Kahe sisendiga XOR on tõene ainult siis, kui sisendväärtused on erinevad, ja väär, kui nad on võrdsed, sõltumata väärtustest. Rohkem kui kahe sisendi puhul on väljundiks tõene, kui sisendis on tõeseid väärtusi paarisarv. Praktikas tehakse selliseid väravaid lihtsamatest loogikaväravatest.
De Morgani teoreem[muuda | muuda lähteteksti]
De Morgani teoreemi järgi saab AND-värava muuta OR-väravaks, kui pöörata ümber sisendi ja väljundi väärtused. Seetõttu on loodud eraldi rühm sümboleid, kus sisendid ja tuuma sümbol on pööratud. Need sümbolid võivad teha loogikaskeemide joonised palju selgemaks.
NAND-väravat saab näidata OR-sümboli abil, lisades väikesed ringid sisenditele, ja NOR-väravat saab näidata AND-värava sümboliga, lisades ringid sisenditesse. See väike ring tähendab loogilist inversiooni ehk NOT-funktsiooni. De Morgani seaduse ekvivalentsuse abiga saab vahetada kõik väravad, kus ringid on mõlemas otsas, ümber teiste, ringideta väravate vastu, muutes diagrammid kergemini loetavaks (kui nt NAND on joonistatud OR-väravana, millel sisendis on mullid, ja -värav AND-väravana, millel on samuti sisendis mullid, siis mullid välistavad üksteist).
Kõiki loogikafunktsioonid saab realiseerida NAND-väravatega (samuti ka NOR-väravatega). De Morgani teoreemi kasutatakse, kui soovitakse loogiline skeem ümber teha ainult NAND- või NOR-väravatel põhinevaks. Seda tehakse eelkõige seepärast, et loogilisi väravaid on väga lihtne osta hulgi (ostes ühte tüüpi väravaid on hind odavam ja kogustega on raskem eksida) ja paljud elektroonikapoed müüvad ainult NAND- ja NOR-väravaid.
Loogikavärav kui mälu[muuda | muuda lähteteksti]
Loogikaväravaid ehk loogikalülisid on võimalik kasutada mäluna andmete salvestamiseks. Selleks peab need ühendama omavahel tagasisideahela abil trigeriks. Triger võimaldab säilitada informatsiooni 1 biti mahus. Mitu ühise juhtimisega trigerit koos moodustavad registri, mis võimaldab säilitada mitmebitilist andmesõna. Elektrilisel tagasisidel põhineva mäluga seadet nimetatakse järjendloogikaseadmeks, sest selle väljund on mõjutatav seadme eelmis(t)e seisundi(te) ehk olekute poolt.
Elektrilisel tagasisidel põhinevaid loogilisi ahelaid tuntakse ka arvuti mäluseadmetena (näiteks register, SRAM, protsessori vahemälu), mille jõudlus (kiirus, keerukus, usaldusväärsus andmete talletamisel) varieerub sõltuvalt rakendusest.
Kolme olekuga loogilised väravad[muuda | muuda lähteteksti]
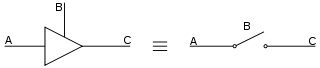
Kolme olekuga loogikaväravatel on kolm erinevat väljundi olekut: kõrge (H), madal (L) ja kõrge-takistus (Z). Kõrge-takistus-olek ei määra loogikas rolli, aga see on kasutusel protsessori andmesiinides, lubamaks mitmel kiibil saata andmeid. Grupp kolme olekuga loogikaväravatest, mis juhivad liini sobiva kontrollskeemiga, on põhimõtteliselt multipleksor. Elektroonikas tähendab väljundi kõrge olek, et väljund saab elektrivoolu positiivsest poolusest, ja väljundi madal olek vastavalt siis, kui väljund saab elektrivoolu negatiivsest poolusest (maandus). Kõrge takistusega olek tähendab, et väljund on lahti ühendatud vooluringist.
Muu[muuda | muuda lähteteksti]
Kasutades ainult NAND- või NOR-väravaid, saab luua ka kõik teised väravad. Algselt oli NAND-värava ehitamine NOR-väravast lihtsam ja seetõttu võetigi laialdaselt kasutusele just NAND, kuigi ka NOR-väravaid kasutatakse tänapäeval üpriski palju. Kuigi teoorias puudub piir, kui palju väravaid saab üksteise järele seadmes istutada, siis praktikas jääb piiravaks seadmes olev ruum, kuhu need väravad paigaldada.
Aastal 1898 esitas Nikola Tesla patendi seadmetele, mis sisaldasid releedel kui juhitavatel lülititel põhinevaid loogikaväravaid. Hiljem asendati releed elektronlampidega.
