Lagrange'i punktid
See artikkel vajab ajakohastamist. |
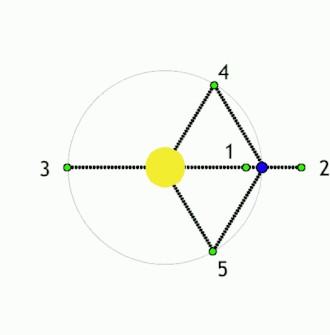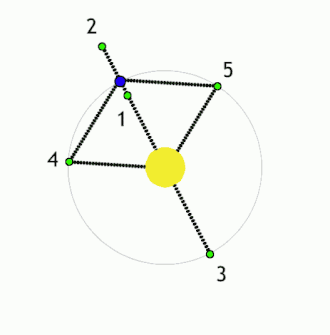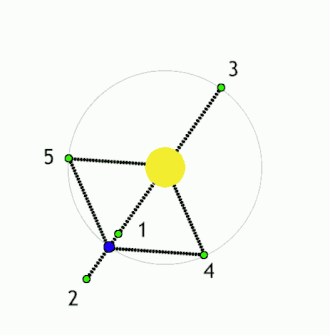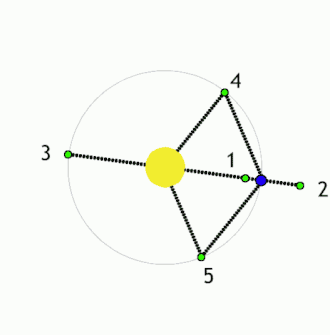

Lagrange'i punktid ehk L-punktid on asukohad ruumis, kus väikese massiga keha saab kahe, teineteise ümber tiirleva, suure massiga keha suhtes paigal püsida. Nendes punktides tasakaalustavad gravitatsioonilised jõud ja orbitaalne liikumine teineteist. Maa-Päikese-süsteemi vaadates oleksid L-punktid sellised, mille tiirlemisperiood on võrdne Maaga (1 aasta) ning mille asukoht Maa ja Päikese suhtes ei muutu. Lagrange'i punkte on kokku 5: L1, L2, L3, L4 ja L5, millest kolm esimest on ebastabiilsed ning kaks viimast stabiilsed punktid.
Ajalugu ja üldine ettekujutus[muuda | muuda lähteteksti]
Esimesed kolm kollineaarset ehk samal sirgel asuvat L-punkti (L1, L2, L3) avastas Šveitsi matemaatik ja füüsik Leonhard Euler. Paar aastat hiljem avastas Itaalia-Prantsusmaa matemaatik ja astronoom Joseph Louis Lagrange, kelle järgi on need punktid ka nime saanud, ülejäänud kaks (L4 ja L5).
Lagrange'i punktid on kolme keha probleemi erijuhud.
Stabiilsed Lagrange'i punktid on punktid, kus tühise massiga keha suudab põhimõtteliselt paigal püsida. Seda võib vaadelda kui nõgusat kausipõhja, kus keerleb üks pingpongipall (pärast mõneajalist liikumist jääb see kausipõhjas seisma).
Lagrange'i punktid[muuda | muuda lähteteksti]
Allolevates alapeatükkides vaatleme Lagrange'i punkte Maa-Päikese-süsteemis.
L1 punkt[muuda | muuda lähteteksti]
L1 punkt asub Maad ja Päikest ühendaval sirgel, nende taevakehade vahel. See on punkt, kus Maa külgetõmbejõud on võrdne Päikese külgetõmbe jõuga ning seetõttu on ta ainus L-punkt, mis eksisteeriks ka statsionaarses süsteemis (ehk süsteemis, kus orbitaalset liikumist ei toimuks). L1 punkt asub Maa-Päikese-süsteemis ligikaudu 1,5 miljonit kilomeetrit Maast Päikese pool ning on ebastabiilne L-punkt ehk sinna on satelliidi või mõne muu keha paigale jätmine üsna keeruline. Kui tavaliselt on Maast Päikesele lähemal olevate kehade tiirlemisperiood väiksem kui Maal (näiteks Merkuuril on see ligikaudu 88 päeva), siis L1 punktis on Maa külgetõmbejõu tõttu periood täpselt niipalju suurem, et see on võrdne Maa tiirlemisperioodiga.
L1 asukoha konkreetse süsteemi jaoks saab leida järgnevast seosest:
kus r on L1 punkti kaugus väiksemast kehast, R on kaugus kahe põhilise keha vahel ja M1 ja M2 on vastavalt suure ja väikese keha massid. Kui väiksema keha mass on suurema keha massist oluliselt väiksem, siis punktid L1 ja L2 asuvad ligikaudu samal kaugusel väiksemast kehast. Nende asukoha saab sellisel juhul määrata valemiga:
L1 punkt sobib hästi Maa-Päikese-süsteemi jälgimiseks, kuna seal ei ole kunagi Maa ega Kuu põhjustatud varjestatust.
L2 punkt[muuda | muuda lähteteksti]
Kui L1 asub Maast Päikese pool, siis L2 punkt paikneb Maad ja Päikest ühendaval sirgel Maast teisel pool, ligikaudu 1,5 miljoni kilomeetri kaugusel. L2 punkt asetseb kohas, kus kehale mõjuvad tsentrifugaaljõud on tasakaalus kahe massiivse keha (Maa ja Päike) summaarse külgetõmbejõuga. L2 asukoha saab määrata allolevast seosest:
Võrrandi parameetrid on samad, mis L1 korral.
Päikese-Maa-süsteemis olev L2 punkt on hea koht kosmoseobservatooriumite paigutamiseks, sest sinna paigutatud sond säilitab Maa ja Päikese suhtes oma asukoha ning on seetõttu paremini kaitstud päiksekiirguste eest. Orbiidil L2 ümber liigub alates 24. jaanuarist 2022 James Webbi kosmoseteleskoop. Maa-Kuu-süsteemi L2 punkt sobiks hästi sidesatelliidiks, mis suudaks ära katta Kuu-taguse ala.
L3 punkt[muuda | muuda lähteteksti]
L3 punkt asub Maad ja Päikest ühendaval sirgel Päikesest nii-öelda tagapool ehk see on ainus Lagrange'i punkt, mida Maalt näha ei saa. Analoogiliselt L2 punktile asetseb see punkt kohas, kus kehale mõjuvad tsentrifugaaljõud on tasakaalus Maa ja Päikese summaarse külgetõmbejõuga.
Võrdsustades keha külgetõmbejõu keha tsentrifugaaljõuga, saab L3 punkti asukoha leida valemist:
- .
Kus R on kaugus kahe massiivse keha vahel, M1 on Suurema keha mass, M2 on väiksema keha mass ning r on kaugus punktist L3 kuni suurema kehani. Kui väiksema keha mass M2 on palju väiksem suurema keha massist M1, siis saab L3 asukoha määrata valemist:
L3 punkti oleks hea panna satelliit, mis annaks infot Päikesel toimuvate arengute kohta ning hoiataks Päikese aktiivsuse eest umbes seitse päeva ette.
L4 ja L5 punktid[muuda | muuda lähteteksti]
Punktid L4 ja L5 paiknevad Maa-Päikese-süsteemis Maaga samal orbiidil. L4 punkt asub Maast 60 kraadi eespool ja L5 60 kraadi tagapool. L4 ja L5 on ainsad stabiilsed punktid. Need punktid on tasakaalus seetõttu, et punktide L4 ja L5 kaugused põhiliste kehadeni on võrdsed. Seega kahe massiivse keha gravitatsiooniliste jõudude suhe on võrdne nende masside suhtega ning resultantjõud on suunatud massiivsete kehade raskuskeskmesse, mis on ühtlasi nende pöörlemiskese. Mainitud resultantjõud on täpselt piisav, et hoida (kahe põhilise kehaga võrreldes) suhteliselt väikese massiga keha orbitaalsel liikumisel ülejäänud süsteemiga tasakaalus.
Päikese-Jupiteri-süsteemis on L4 ja L5 punktides mitmeid tuhandeid asteroide, mida kutsutakse Trooja asteroidideks. Enamik asteroide on oma nime saanud Trooja sõja tegelaste järgi, kusjuures L4 punktis ehk Jupiterist 60 kraadi eespool on kreeklaste leer ning 60 kraadi tagapool on troojalaste leer.
Ühe teooria järgi on ka Kuu tekkimine seotud Lagrange'i punktidega. Väidetavalt oli kunagi olnud Theia nimeline keha, mis paiknes Maa-Päikese-süsteemi L4 või L5 punktis. Pärast oma stabiilsuse kaotamist põrkus see Maaga ning pärast põrget jäi ümber Maa tiirlema, moodustadeski Kuu.[1]
Kosmosemissioonid Lagrange'i punktidesse[muuda | muuda lähteteksti]
L1[muuda | muuda lähteteksti]
- ISEE-3 (International Sun/Earth Explorer 3), praegu tuntud kui ICE (International Cometary Explorer). NASA ja ESA/ESRO ühisprojekti uurimisobjektiks oli Maa magnetvälja ja päikesetuule vastastikune mõju. Sondi paiknemine L1-punktis: 12. august 1978 – 10. juuni 1982. ISEE-3 oli ka esimene satelliit, mis paiknes halo orbiidil.[2]
- NASA projekt Genesis kogus päikesetuule osakeste proove ja tõi need Maale uurimiseks. Paiknemine L1-punktis: 16. november 2001 – 8. september 2004. [3]
- NASA satelliidi WIND eesmärk on uurida kiirgusi ja plasmat päikesetuules ja Maa magnetosfääris. Missioon algas 1. novembril 1994. [4]
- ESA ja NASA ühisprojektina valminud SOHO tegeleb Päikese arengute uurimisega. Missioon algas 2. detsembril 1995. [5]
- ACE (Advanced Composition Explorer) on NASA projekt, mille ülesandeks on uurida päikesetuult ja hoiatada päikesetormide eest. Missioon algas 25. augustil 1997. [6]
- DSCOVR (Deep Space Climate Observatory) on NASA / NOAA projekt, mille ülesandeks on uurida kosmoseilma ning vaadelda Maa Päikese poolt valgustatud külge. Vaatlused algasid juulis 2015. [7]
L2[muuda | muuda lähteteksti]
- WIND
- Chang'e on Hiina kosmoseprojekt, mis algselt tegeles Kuu uurimisega. Paiknemine L2-punktis: 25. august 2011 – aprill 2012.
- WMAP on NASA kosmoseaparaat, mis tegeleb kosmilise mikrolaine-taustkiirguse uurimisega. Paikneb L2 punktis alates 1. oktoobrist 2001.
- Plancki observatoorium on Euroopa Kosmoseagentuuri sond, mis tegeleb kosmilise mikrolaine-taustkiirguse uurimisega. Paikneb Maa-Päikese-süsteemi L2 punktis alates juulist 2010. [8]
- Herscheli kosmoseobservatoorium on ESA sond, mis uurib kosmoseavarusi infrapuna lainepikkustel. Päikese-Maa-süsteemi L2 punktis paikneb satelliit alates 2009. aasta juulist ning arvatavasti lõpeb selle missioon 2013. aastal. [9]
- James Webbi kosmoseteleskoop
L3[muuda | muuda lähteteksti]
Kunagi arvati, et Päikese-Maa-süsteemis paikneb just selles punktis n-ö Maa vastukaal ehk Maa-sugune planeet, mis paikneb teisel pool Päikest. Kosmoseuuringud on aga välja selgitanud, et sellist taevakeha olemas ei ole. Tehiskaaslaste paigutamiseks on see ebasoodne koht, sest side pidamine on raskendatud.
L4 ja L5[muuda | muuda lähteteksti]
L4 ja L5 punktides paiknevad enamasti asteroidid ja sinna kogunevad kosmosetolmu pilved, mistõttu ei ole need väga soodsad paigad satelliitide paigutamiseks.
Kosmosemaanteed[muuda | muuda lähteteksti]
Tulevikus võivad Lagrange'i punktide üheks suuremaks rakendusalaks saada kosmosereisid gravitatsioonikoridoride kaudu. Gravitatsioonikoridorid seovad omavahel erinevate kehade süsteemide erinevaid Lagrange'i punkte. Need koridorid on L-punktide juures kitsad ning vahepealsel alal laiemad. Gravitatsioonikoridore ehk kosmosemaanteid võib võrrelda ookeani hoovustega. Kui mingil orbiidil liikudes satutakse risti mõne koridoriga, siis väikese kütusekuluga saab liikumistrajektoori nii palju muuta, et see koridor kannab sondi kuni järgmise Lagrange'i punktini, just nagu hoovus kannab purjelaeva. Seda tehnoloogiat kasutades oleks võimalik kosmosereisidel kütusekulu vähendada ligikaudu 10 korda. Siiski pole gravitatsioonikoridoride kasutamine täiesti ilma puudusteta – sobiva koridori leidmiseks võib kuluda väga palju aega. Näiteks Maa orbiidilt Marsile jõudmiseks ilma kütust kasutamata kuluks tuhandeid aastaid. Seega täiesti ilma kütust kasutamata ei ole kosmosereisid siiski veel väga realistlikud. Seni on gravitatsioonikoridore kasutatud näiteks NASA sondi Genesis liigutamiseks. [10]
Viited[muuda | muuda lähteteksti]
- ↑ "Kuu moodustamise teooria". Originaali arhiivikoopia seisuga 2. jaanuar 2013. Vaadatud 29. jaanuaril 2013.
- ↑ ISEE-3
- ↑ Genesis
- ↑ WIND
- ↑ "SOHO". Originaali arhiivikoopia seisuga 18. september 2021. Vaadatud 29. jaanuaril 2013.
- ↑ ACE
- ↑ DSCOVR: Deep Space Climate Observatory
- ↑ Planck'i kosmoseobservatoorium
- ↑ Herschel'i kosmoseobservatoorium
- ↑ Gravitatsioonikoridorid
Välislingid[muuda | muuda lähteteksti]
| Pildid, videod ja helifailid Commonsis: Lagrange'i punktid |
- ESA versioon Lagrange'i punktide tutvustusest (Heade animatsioonidega veebileht)
- Essee kolme keha probleemi kohta (J.-L. Lagrange'i essee ingliskeelne tõlge)


![{\displaystyle r\approx R{\sqrt[{3}]{\frac {M_{2}}{3M_{1}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1175643479ba922598c78a6d4dfcf7fff160bfe7)


