Ülilühike impulss
Ülilühike impulss ehk femtosekundimpulss on elektromagnetlainete impulss, mille ajaline kestus (fikseeritud punktis) on femto- või pikosekundi suurusjärgus. Selle aja jooksul jõuab elektriväli teha vaid mõned võnked (nähtava valguse jaoks alla miljoni) [1] ning energia on kontsentreeritud väga väiksesse piirkonda. Seega on üldjuhul ülilühikestes impulssides väga suured elektrivälja tugevused, mis toob kaasa mittelineaarsed efektid. Määramatuse printsiibi tõttu on ülilühikestele impulssidele iseloomulik väga lai spekter.
Kirjeldus[muuda | muuda lähteteksti]
Aja ruumis[muuda | muuda lähteteksti]
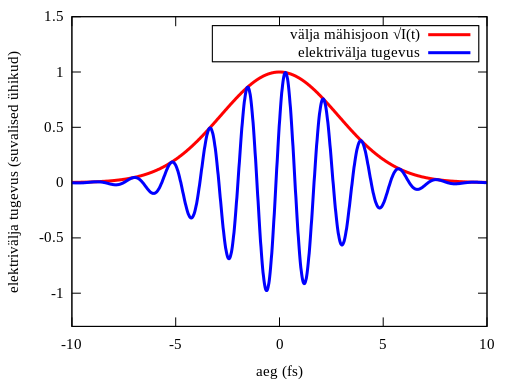
Üldiselt saab suvalist elektromagnetlainet kirjeldada selle elektriväljaga , kuid ülilühikeste impulsside kontekstis pakub enamasti huvi fikseeritud polarisatsiooniga elektrivälja ajaline sõltuvus ühes ruumipunktis ning sel juhul toimib elektrivälja skalaarlähendus hästi. Skalaarse elektrivälja saab omakorda lahti kirjutada kujul
kus tähistab välja intensiivsust, on impulsi mähisjoon, on impulsi keskmine ringsagedus (kandesagedus) ning on laine faas. Impulsi mähisjoone määrab , kuid spektri määravad peamiselt ning . Koosinuse argumendi muutumiskiirust nimetatakse impulsi hetkringsageduseks. Sageli kirjutatakse elektriväli välja komplekskujul , millest reaalne väli on reaalosa.
Sagedusruumis[muuda | muuda lähteteksti]
Teine võimalus ülilühikest impulssi kirjeldada on Fourier' pöörde abil sagedusruumis:
kus on impulsi spektraalne võimsustihedus ehk spekter ning on spektraalfaas. Nii spektraalne võimsus kui ka faas mõjutavad impulsi kuju ning kestust ajalises esituses. Spektraalse faasi tuletis sageduse järgi , mida nimetatakse ka rühmaviibeks, iseloomustab vastava ringsagedusega lainekomponendi viibimist aja nullpunkti suhtes.[1]
Aja-ribalaiuse korrutis[muuda | muuda lähteteksti]
Aja-ribalaiuse korrutiseks (ARK) nimetatakse impulsi kestust iseloomustava aja standardhälbe ning spektraalset laiust iseloomustava sageduse standardhälbe korrutist . Kuna aja nihete ja skaleerimise ning väljatugevuse skaleerimise korral jääb impulsi ARK muutumatuks, iseloomustab see impulsi kuju ning keerukust. Sama spektriga impulssidest on kõige väiksem ARK sellistel, mille spektraalne faas on konstantne.[2]
Sirts[muuda | muuda lähteteksti]

ARK ja seega ka impulsi keerukus sõltuvad peamiselt impulsi faasist. Vaadeldes täpsemalt spektraalset faasi , saab selle Taylori reana lahti kirjutada:
kus , ning analüüsida iga liikme mõju impulsile eraldi.
- kutsutakse absoluutseks faasiks, ehk mähisjoone faasiks. Absoluutne faas saab oluliseks mittelineaarsetes protsessides siis, kui impulsi pikkus on vaid paar võnketsüklit. Paljude võnketsüklitega impulsside korral ei mõjuta absoluutne faas kvalitatiivselt impulsi kuju ning on seega ebaoluline.
- määrab impulsi hilinemise kokkuleppelise aja alguspunkti suhtes ning ei mõjuta impulsi kuju.
- ja ka kõik järgnevad liikmed tekitavad sirtsu: impulsi kestuse pikenemist ning hetksageduse erinevust impulsi eri punktide vahel. Kuna iga sageduskomponendi viibe määrab spektraalse faasi tuletis sageduse järgi, tekitab faasi ruutliige sageduste ning nende saabumisaegade vahele võrdelise seose. Tugeva sirtsu korral , kus on samasuguse spektri, aga konstantse faasiga impulsi ajaline kestus, avaldub impulsi hetksagedus kujul .
- on faasi kuupliige. See tekitab impulsile ajalises esituses palju väiksemaid eel- või järelimpulsse, mida saab kasutada koherentkontrollis.
Kui eesmärgiks on saada võimalikult lühike impulss, siis on oluline kõrgemat järku liikmed kompenseerida.[2]
Mõõtmine[muuda | muuda lähteteksti]
Ülilühikeste impulsside mõõtmiseks on erinevaid meetodeid, mis laias laastus jagunevad kolme kategooriasse: mittetäieliku taastamise meetodid, etalonimpulssi kasutavad täieliku taastamise meetodid ning iseseisvad täieliku taastamise meetodid. Mittetäieliku taastamise meetodid annavad vaid jämeda hinnangu impulsi kestusele; etalonimpulssi kasutavad täieliku taastamise meetodid rekonstrueerivad küll impulsi täieliku kuju, nii intensiivsuse kui ka faasiinfo, kuid kasutavad selleks juba täielikult karakteriseeritud etalonimpulssi, ning võimsaimad kolmest, täieliku taastamise meetodid, karakteriseerivad täielikult impulsi kasutamata välist etalonimpulssi.
Mittetäieliku taastamise meetodid[muuda | muuda lähteteksti]
Autokorrelatsioon on üks vanemaid ja lihtsamaid meetodeid impulsi pikkuse hindamiseks. Impulss jagatakse Michelsoni interferomeetris kaheks identseks komponendiks, mille vahele tekitatakse ajaline muudetav viive . Mittelineaarses anisotroopses kristallis tekitatakse nende elektriväljade korrutisega võrdeline elektriväli, mille keskmist intensiivsust mõõdetakse fotodioodiga. Kui on väike, siis impulsid kattuvad ning mõõdetud autokorrelatsioon on maksimaalne, kui aga on suurem impulsi pikkusest, siis impulsid ei kattu ning mõõdetud autokorrelatsioon on null.
Ristkorrelatsioon on muidu täpselt analoogne autokorrelatsiooni meetodiga, aga üks mittelineaarsele kristallile langev impulss on asendatud lühema testimpulsiga. Sel juhul mõõdab fotodiood uuritava impulsi intensiivsuse korrelatsiooni lühema impulsiga, mis sarnaneb seda enam tegeliku intensiivsuspildiga, mida lühem on testimpulss.
Nii auto- kui ka ristkorrelatsiooni meetodi puuduseks on see, et nendega ei ole võimalik mõõta impulsi faasi. [2]
Etalonimpulssi kasutavad täieliku taastamise meetodid[muuda | muuda lähteteksti]
Spektraalne interferomeetria on eksperiment, milleks on vaja vaid spektromeetrit ning teadaoleva spektri ning faasiga etalonimpulssi. Mõõtmine toimub kahes osas. Esmalt mõõdetakse spektromeetriga impulsi võimsusspekter . Seejärel liidetakse mõõdetavale impulsile viibega otsa etalonimpulss ning mõõdetakse tekkinud liitimpulsi spekter.
Mõõdetud liitimpulsi spekter on koosinusliikme tõttu perioodiline keskmise ringsagedusega ( suhtes), mida moduleerib impulsi suhteline faas etalonimpulsi suhtes. Kuna impulsi spektraalne võimsus sai esimese sammuna mõõdetud ning etalonimpulsi spekter ning faas on teada, saab selle mõõtmise tulemusest avaldada tundmatu impulsi faasi näiteks Fourier' filtreerimise teel. Sellel meetodil on mõningad piirangud. Esiteks, et saaks üldse jälgida etalonimpulsi ning mõõdetava impulsi vahelist interferentsi, peavad need olema koherentsed (tekitatud sama laseri poolt). Teiseks, kuna faasi saab määrata vaid nendel sagedustel, kus etalonimpulsi spektraalne võimsus ei ole null, peab etalonimpulss olema mõõdetavast laiema spektriga.
Fourier' teisenduse spektroskoopia on samuti meetod, mille kasutamiseks on vaja tuntud etalonimpulssi, kuid ei ole vaja spektromeetrit. Ka see meetod koosneb kahest sammust. Esmalt mõõtetakse tundmatu impulsi, millele on lisatud selle võrra viibinud koopia, intensiivsuse sõltuvus viibest:
kus tähistab sidumit ning on kaaskompleks. Seejärel liidetakse tundmatule impulsile erinevate viivete juures etalonimpulss ning mõõdetakse intensiivsuse sõltuvus:
Fourier' pööre annab spektraalse võimsustiheduse ning Fourier' pöörde argument annab spektraalfaasi . Ka selle meetodi puuduseks on, et on tarvis mõõdetava impulsiga koherentset etalonimpulssi, mille spekter on laiem kui mõõdetaval impulsil. [2]
Iseseisvad täieliku taastamise meetodid[muuda | muuda lähteteksti]
FROG (Frequency Resolved Optical Gating) on vanim meetodite klass ülilühikese impulsi täielikuks määramiseks ilma etalonimpulsi abita. Selle tööpõhimõtteks on kasutada teist, strobeerivat impulssi , millega eraldatakse mõõdetavast impulsist lõik, ning mõõta saadud lõigu spekter. FROG-i mõõdetud signaal avaldub kujul
kus tähistab strobeeriva impulsi ning mõõdetava impulsi vahelist viivet. Mõõdetud signaalist taastatakse tegelik elektriväli iteratiivsete algoritmide abil. Peamine erinevus erinevate FROG meetodite vahel on strobeeriva impulsi valik. Tüüpiliste näidetena võib strobeerivaks impulsiks olla mõõdetava impulsi amplituudi ruut (PG-FROG), mõõdetav impulss ise (SHG-FROG), mõni teine tuntud või tundmatu impulss (XFROG).
SPIDER (Spectral Phase Interferometry for Direct Electric-field Reconstruction) on analoogne spektraalse interferomeetriaga, kuid selle puhul kasutatakse etalonimpulsi asemel mõõdetavat impulssi, mis on nii ajas ( võrra) kui ka sagedusruumis ( võrra) originaali suhtes nihutatud. Sel juhul moduleerib mõõdetud spektri piikide sagedust .
Seega saab mõõtetulemustest leida , mida integreerides saab leida spektraalse faasi. [2]
Vormimine[muuda | muuda lähteteksti]

Et ülilühikesi impulsse optimaalselt kasutada, on enamasti vaja, et need oleksid antud rakenduse jaoks sobiva kujuga. Selleks on vaja neid vormida. Lihtsamad vormimismeetodid põhinevad lineaarsetel nihkeinvariantsetel filtritel. Nende puhul avaldub süsteemi väljundimpulss sisendimpulsi ja süsteemi koste sidumine. Sagedusesituses asendub sidum lihtsa korrutamisega , kus .
Lihtsamad filtrid ei ole programmeeritavad ning nende kostet ei saa muuta. Nende näideteks on
- Michelsoni interferomeeter, mis tekitab kaks esialgsega identset impulssi, millel on ajaline vahe.
- dispergeeriv keskkond, näiteks klaasitükk. , kus on materjali murdumisnäitaja ning tüki paksus.
- võrekompressor, mis koosneb kahest paralleelsest difraktsioonvõrest ning peeglist, millelt mõlemalt difraktsioonvõrelt peegeldunud valgus tagasi peegeldatakse. Tööpõhimõte seisneb selles, et erineva lainepikkusega valguse komponendid läbivad süsteemis erineva teepikkuse. , kus on võredevaheline kaugus, on kiire esimesele võrele langemise nurk ning on vastava komponendi peegeldusnurk difraktsioonivõrelt.
- sirtsuga peegel, mis koosneb sobivalt valitud paksusega dielektriku kihtidest. sõltub materjali peegeldustegurist ning saab disainida sobiva kihtide paksuse valikuga.
Keerulisemad filtrid koosnevad mõnest programmeeritavast elemendist ning nende kostet saab vastavalt vajadusele muuta. Levinuim neist on niinimetatud 4f Fourier' vormija. See koosneb kahest identsest difraktsioonvõrest ning kahest identsest kumerläätsest. Ääres olevad difraktsioonvõred asuvad läätsedest ühe fookuskauguse kaugusel ning läätsed üksteisest omakorda kahe fookuskauguse kaugusel, sellest ka selle nimetus. Täpselt läätsede vahele, Fourier' tasandile paigutatud maski abil saab muuta süsteemi kostet. Kasutatud mask võib olla ka programmeeritav. 4f Fourier' vormija ja ka teiste programmeeritavate vormijate puuduseks on nende ajaline ja ruumiline sidestus: ajalise koste muutmisega muutub ka impulsi ristläbilõige. [2]
Rakendused[muuda | muuda lähteteksti]
Sobiva ajalis-ruumilise kujuga ülilühikesed impulsid leiavad rakendust paljudel aladel, näiteks järgmistel:
- koherentkontroll (ingl k coherent control) ehk nanoskaalal toimuvate dünaamiliste protsesside kontrollimine [3][4][5]
- mitmedimensiooniline spektroskoopia [6]
- mikroskoopia [7]
- optiliste impulsside kokkusurumine [8]
- arvude tegurdamine [9][10]
- optiline sidetehnika [11]
Viited[muuda | muuda lähteteksti]
- ↑ 1,0 1,1 Trebino, R. (2000). Frequency-Resolved Optical Gating: The Measurement of Ultrashort Laser Pulses. Boston, MA: Springer US. doi:10.1007/978-1-4615-1181-6
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 Monmayrant, A., Weber, S., & Chatel, B. (2010). A newcomer’s guide to ultrashort pulse shaping and characterization. Journal of Physics B: Atomic, Molecular and Optical Physics, 43(10), 103001. doi:10.1088/0953-4075/43/10/103001
- ↑ Goswami, D. (2003). Optical pulse shaping approaches to coherent control. Phys. Rep. 374 385
- ↑ Ohmori, K. (2009). Wave-packet and coherent control dynamics. Annu. Rev. Phys. Chem. 60 487–511
- ↑ Dantus, M., & Lozovoy V. V. (2004). Experimental coherent laser control of physicochemical processes. Chem. Rev. 104 1813–59
- ↑ Shim, S.-H., & Zanni, M. T. (2009). How to turn your pump-probe instrument into a multidimensional spectrometer: 2D IR and VIS spectroscopies via pulse shaping. Phys. Chem. Chem. Phys. 11 748–61
- ↑ Silberberg, Y. (2009). Quantum coherent control for nonlinear spectroscopy and microscopy. Annu. Rev. Phys. Chem. 60 277–92
- ↑ Efimov, A., Moores. M. D., Mei, B., Krause, J. L., Siders, C. W., & Reitze, D. H. (2000). Minimization of dispersion in an ultrafast chirped pulse amplifier using adaptive learning. Appl. Phys. B 70 S133
- ↑ Weber, S., Chatel, B., & Girard, B. (2008). Factoring numbers with interfering random waves. EuroPhys. Lett. 83 34008
- ↑ Bigourd, D., Chatel, B., Girard, B., & Schleich, W. P. (2008). Factorization of numbers with the temporal Talbot effect: optical implementation by a sequence of shaped ultrashort pulses. Phys. Rev. Lett. 100 030202
- ↑ Sardesai, H. P., Chang, C. C., & Weiner, A. M. (1998). A femtosecond code division multiple-access communication system test bed. J. Lightwave Technol. 16 1953


















![{\displaystyle \varphi _{n}=\left[{\frac {{\text{d}}^{n}\varphi }{{\text{d}}\omega ^{n}}}\right]_{\omega =\omega _{0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac86a3e7ae37bcf211e1920185ba8a98f2342cd2)










![{\displaystyle I(\omega )=\left|{\widetilde {\mathcal {E}}}(\omega )+{\widetilde {\mathcal {E}}}_{\text{etal}}(\omega )e^{i\omega \tau }\right|^{2}=S(\omega )+S_{\text{etal}}(\omega )+2{\sqrt {S(\omega )S_{\text{etal}}(\omega )}}\cos \left[\varphi (\omega )-\varphi _{\text{etal}}(\omega )-\omega \tau \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4860e2764a3be968709ca999433ed62b5d0ab59a)


















![{\displaystyle I(\omega )=\left|{\widetilde {\mathcal {E}}}(\omega )+{\widetilde {\mathcal {E}}}(\omega )e^{i\omega \tau }\right|^{2}=2S(\omega )\left(1+\cos \left[\varphi (\omega )-\varphi (\omega -\Omega )-\omega \tau \right]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87fa8d262b0ddbf6a7fb7af33d2fd9effdfc74d9)













